実際に質量-ばね-ダンパーシステムの運動を計算する

今回は質量-ばね-ダンパーシステムについて、例を用いて実際に値を計算していきたいと思います。

質量-ばね-ダンパーシステムについての解説は、こちらの記事を参考にしてください。

質量-ばね-ダンパーシステムの運動を求める 今回は質量-ばね-ダンパーシステム（Damped Mass Spring System）を用いて、モデルの振動（運動）について考...

質量-ばね-ダンパーシステム

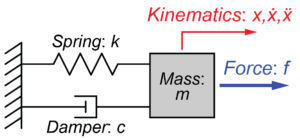
今回はこちらの質量-ばね-ダンパーモデルを用いて、システムの運動を求めていきます。

各パラメータの値は、質量\(m = 5 [kg]\)、ダンパー\(c = 10 [\frac{N}{m/s}]\)、ばね\(c = 100 [\frac{N}{m}]\)とします。

このシステムについて、時刻\(t=0\)で質量\(m\)を変位\(x=x_0=0.1[m]\)で静かに離した時のシステムの運動を計算していきます。

また計算結果からシステムの振動の様子が分かると思います。

システムの運動方程式を解く

以前に算出した質量-ばね-ダンパーシステムの運動方程式

$$ \ddot{x}(t) + \frac{c}{m} \dot{x}(t) + \frac{k}{m} x(t) = 0 $$

に今回のパラメータを代入すると、

$$ \ddot{x}(t) + 2 \dot{x}(t) + 20 x(t) = 0 $$

となります。

この微分方程式について、

$$ x(t) = e^{ \lambda t} $$

として、\(\lambda\)について解くと、

$$ \ddot{x}(t) + 2 \dot{x}(t) + 20 x(t) = 0 $$

$$ \Rightarrow \lambda^2 + 2 \lambda + 20 = 0 $$

$$ \Rightarrow \lambda = -1 \pm 4.359 i $$

となります。

2つの\(\lambda\)の値が複素数なので、今回のシステムは不足減衰システムとなり、変位\(x(t)\)の一般解は、

$$ x(t) = e^{- \frac{c}{2 m} t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right) $$

となります。

システムの運動を求める

不足減衰システムの一般解にシステムの各パラメータを入力すると、

$$ x(t) = e^{- t} \left( A \cos(4.359 t) + B \sin(4.359 t) \right) $$

となります。

初期条件から残りのAとBを求めていきます。

時刻\(t=0\)で変位\(x(0)\)は、

$$ x(0)=x_0=0.1[m] $$

なので、

$$ x(0) = e^{- 0} \left( A \cos(4.359 \cdot 0) + B \sin(4.359 \cdot 0) \right) = 0.1 $$

$$ \Rightarrow A = 0.1 $$

となります。

時刻\(t\)での速度\(\dot{x}(t)\)は、

$$ \dot{x}(t) = – e^{- t} \left( A \cos(4.359 t) + B \sin(4.359 t) \right) + e^{- t} \left( – 4.359 A \sin(4.359 t) + 4.359 B \cos(4.359 t) \right) $$

となります。

時刻\(t=0\)で速度\(\dot{x}(0)=0\)なので、

$$ \dot{x}(0) = A + 4.359 B = 0 $$

$$ \Rightarrow B = – \frac{A}{4.359} = – 0.0229 $$

となります。

よって、今回のシステムの運動\(x(t)\)は、

$$ x(t) = e^{- t} \left( 0.1 \cos(4.359 t) – 0.0229 \sin(4.359 t) \right) $$

となります。

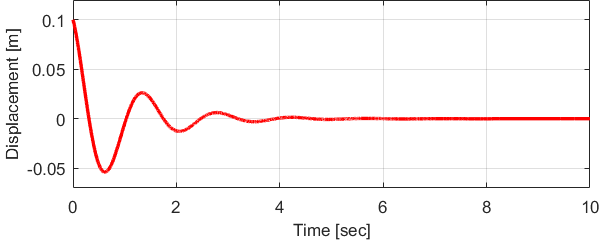
横軸を時間\(t [sec]\)、縦軸を変位\(x [m]\)としてグラフにすると下のようになります。

まとめ

今回は、質量-ばね-ダンパーシステムについて、例を用いて実際に運動を計算する方法を紹介しました。

今回のシステムでは不足減衰システムとなり、初期位置の変位\(x=x_0\)から振動しながら徐々に変位\(x=0\)に近づくことが分かりました。