質量-ばね-ダンパーシステムの運動を求める

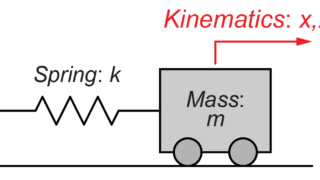
今回は質量-ばね-ダンパーシステム（Damped Mass Spring System）を用いて、モデルの振動（運動）について考えていきたいと思います。

シンプルな質量-ばね-システムを用いた前回の記事はこちら

質量-ばねシステムの振動を求める 今回はシンプルな質量-ばねシステム（Mass Spring System）を用いて、このモデルの振動について算出していきたいと思...

質量-ばね-ダンパーシステムの運動方程式

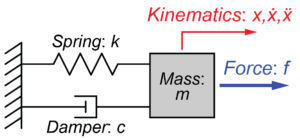
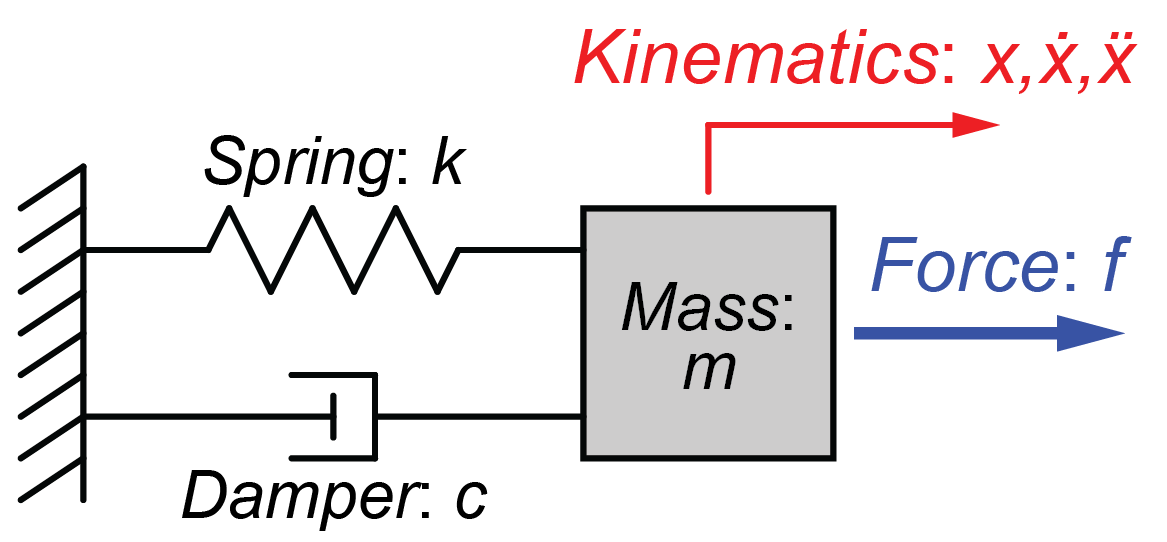
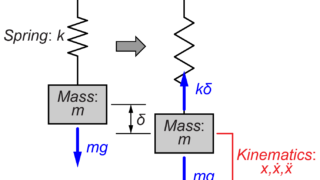
今回は図のように質量\(m\)がばね\(k\)とダンパー\(c\)で壁に接続されているモデルを扱います。

このシステムの質量\(m\)の運動方程式を求めていきます。

質量\(m\)の変位を\(x\)、速度を\(\dot{x}\)とすると、ばね\(k\)とダンパー\(c\)による力は、

$$ k x + c \dot{x} $$

となります。

よって、このシステムの運動方程式は加速度\(\ddot{x}\)を用いて、

$$ m \ddot{x} = – k x – c \dot{x} $$

と表すことが出来ます。

この運動方程式を基にシステムの運動を算出していきます。

質量-ばね-ダンパーシステムの微分方程式

質量-ばね-ダンパーシステムの運動方程式を整理すると、

$$ \ddot{x}(t) + \frac{c}{m} \dot{x}(t) + \frac{k}{m} x(t) = 0 $$

と表すことが出来ます。

この線形微分方程式を変位\(x(t)\)について解いていきます。

変位\(x(t)\)を、

$$ x(t) = e^{ \lambda t} $$

と置くと、上記の線形微分方程式は、

$$ \ddot{x}(t) + \frac{c}{m} \dot{x}(t) + \frac{k}{m} x(t) = 0 $$

$$ \Rightarrow \lambda^2 e^{ \lambda t} + \frac{c}{m} \lambda e^{ \lambda t} + \frac{k}{m} e^{ \lambda t} = 0 $$

$$ \Rightarrow \lambda^2 + \frac{c}{m} \lambda + \frac{k}{m} = 0 $$

と置き換えることが出来ます。

この方程式を\(\lambda\)について解くと、

$$ \lambda = – \frac{c}{2 m} \pm \frac{1}{2} \sqrt{\left( \frac{c}{m} \right)^2 – \frac{4 k}{m} } $$

となります。

この求めた\(\lambda\)の値を先ほど定義した\(x(t)\)の式に代入することでシステムの運動がわかります。

ここで、\(\lambda\)の値によって３パターンの解\(x(t)\)が存在します。

質量-ばね-ダンパーシステムの3パターンの解

質量-ばね-ダンパーシステムの解は定数の値によって、3パターンに分類されます。

1. \(\lambda =\)実数
2. \(\lambda_1 = \lambda_2\)
3. \(\lambda =\)複素数

\(\lambda\)が実数の場合

\(\lambda_1\)と\(\lambda_2\)が実数の場合、求められる解\(x(t)\)は、

$$ x(t) = C_1 e^{- \lambda_1 t} + C_2 e^{- \lambda_2 t}$$

と表すことが出来ます。

この時の変位\(x(t)\)は時間\(t\)の増加とともに徐々に減衰していきます。

このようなシステムを加減衰システム（Overdamped System）といいます。

\(\lambda_1 = \lambda_2\)の場合

\(\lambda_1\)と\(\lambda_2\)が等しい場合、このシステムを臨界減衰システム（Critically Damped System）と言います。

\(\lambda_1\)と\(\lambda_2\)が等しくなるために、下記の関係が成り立ちます。

$$ \left( \frac{c}{m} \right)^2 – \frac{4 k}{m} $$

$$ \Rightarrow c = 2 \sqrt{k m} $$

となります。

この時の\(c\)の値を臨界減衰係数\(c_{CR}\)と言います。

臨界減衰システムの場合（\(\lambda_1 = \lambda_2 = \lambda \)）の解\(x(t)\)は、

$$ x(t) = C_1 e^{- \lambda t} + C_2 t e^{- \lambda t}$$

と表されます。

\(\lambda\)が複素数の場合

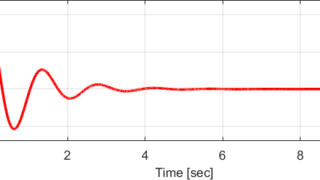
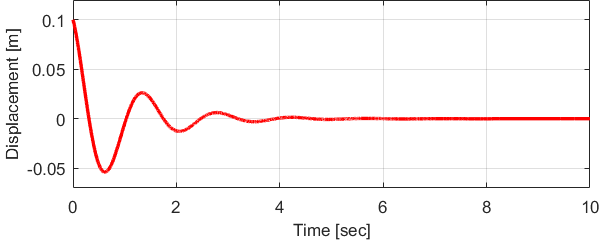
\(\lambda_1\)と\(\lambda_2\)が複素数の場合、このシステムを不足減衰システム（Underdamped Systeｍ）と言います。

複素数の\(\lambda\)の値を

$$ \lambda = \alpha \pm \beta i $$

とすると、求める解\(x(t)\)は、

$$ x(t) = e^{- \frac{c}{2 m} t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right) $$

と表すことが出来ます。

まとめ

今回は、質量-ばね-ダンパーシステムを用いて、システムの運動を表す式を算出する方法を紹介しました。

質量-ばね-ダンパーシステムは、モデルの定数（パラメータ）の値によって、3種類の動作に分類することが出来ます。

次回は、具体的な値を使って、質量-ばね-ダンパーシステムの動きを実際に計算していきたいと思います。

実際に質量-ばね-ダンパーシステムの運動を計算する 今回は質量-ばね-ダンパーシステムについて、例を用いて実際に値を計算していきたいと思います。 質量-ばね-ダンパー...