前回は横向き(水平方向)の質力-ばねシステムの振動について紹介しました。
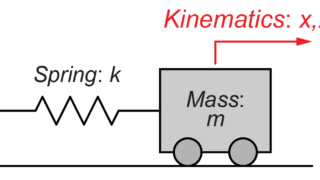
今回は、縦向き(鉛直方向)の質量-ばねシステムの振動を考えていきたいと思います。
鉛直質量-ばねシステム
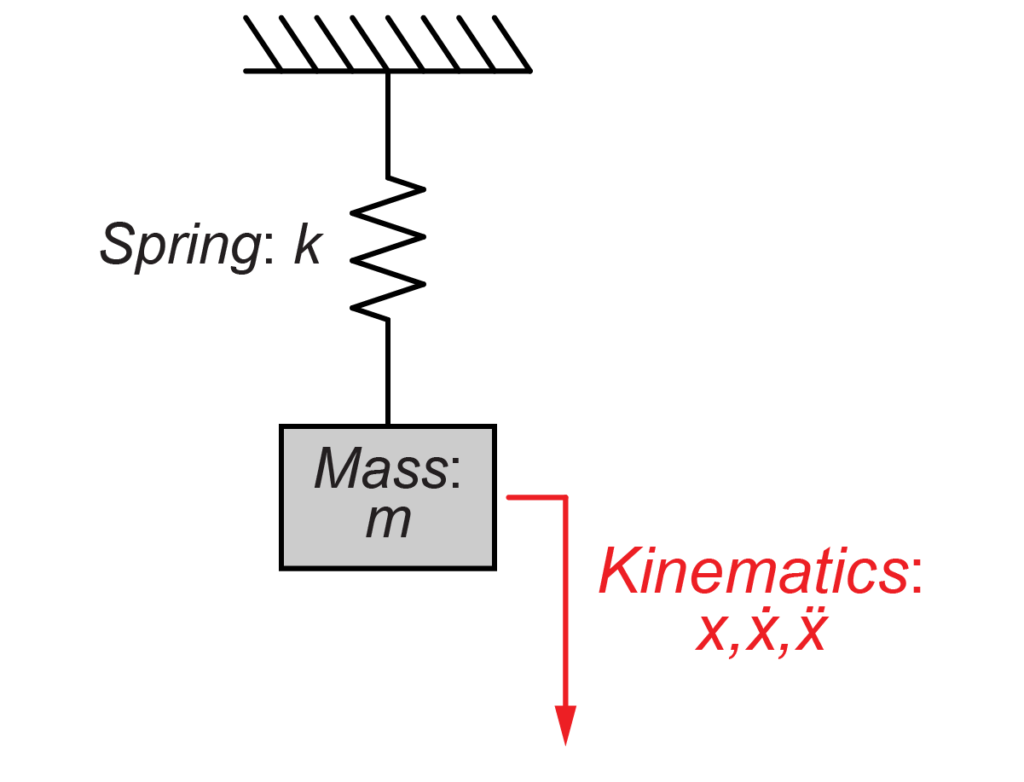
図のような質量mとばねkのシステムを考えていきます。
前回の水平モデルでは、ばねkの力のみを考えました。
今回の鉛直モデルでは、ばねkの力に加えて、質量mにかかる重力を考慮する必要があります。
重力による影響
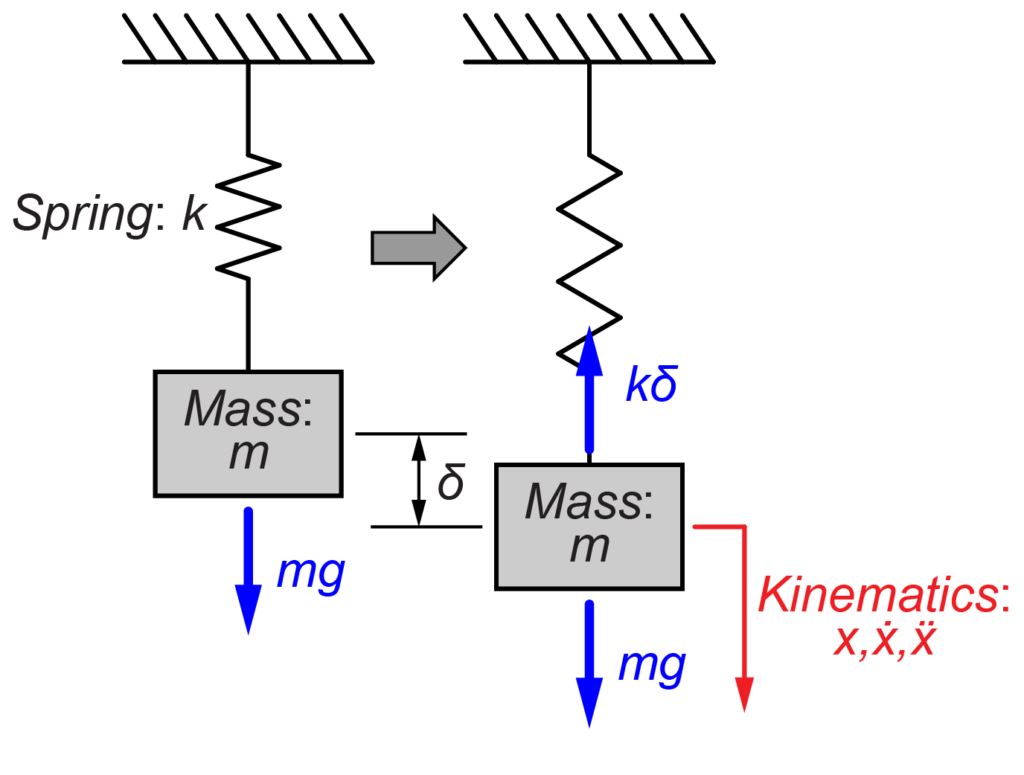
質量mにかかる重力fgは重力加速度gを用いて、
$$ f_g = mg $$
表すことが出来ます。
この重力mgとばねkによる力のつり合う位置δとの関係は、
$$ mg = k \delta $$
となります。
鉛直質量-ばねシステムの振動モデル
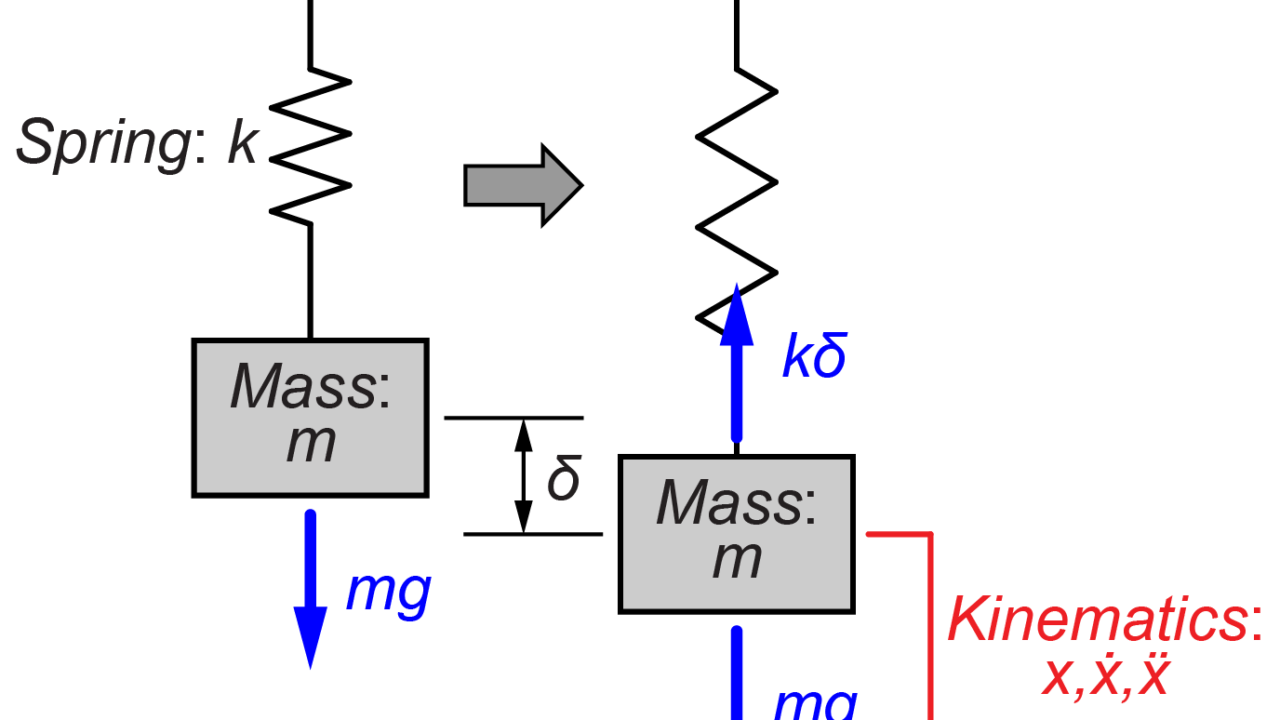
重力mgとばねkがつり合った点δからの質量mの変位をxとして、質量mの運動方程式を求めます。
質量mにかかる力は重力mgとばねkによる力fkです。
このばねkによる力fkは、
$$ f_k = -k \left( x+\delta \right) $$
となります。
よってシステムの運動方程式は、
$$ \begin{eqnarray} ma &=& F \\ &\Rightarrow& m \ddot{x}(t) = mg -k \left( x(t)+\delta \right) \end{eqnarray} $$
となります。
ここで、重力mgとばねkとの釣り合う関係式より、重力mgとばねkと変位δによる力は打ち消し合うため、システムの運動方程式は、
$$ m \ddot{x}(t) = -k x(t) $$
と表すことが出来ます。
この運動方程式は、水平方向の質量-ばねシステムの場合と同じになっています。
そのため、この微分方程式を解いて求める運動(振動)を表す式も同じになります。
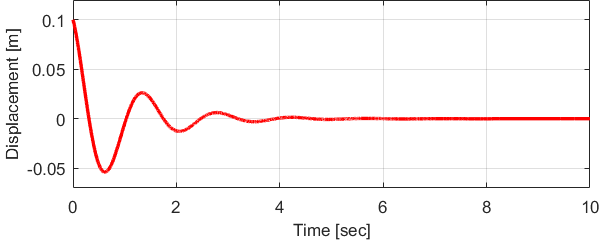
よって、鉛直方向の質量-ばねシステムにおいて、初期変位x0の場合の変位x(t)の運動(振動)式は、
$$ x(t) = x_0 cos \left(\sqrt{ \frac{k}{m} } t \right) $$
と表すことが出来ます。
まとめ
今回は、鉛直方向の質量-ばねモデルについて、システムの動き(振動)を求めてみました。
水平方向の場合と違い、鉛直方向の場合は重力の影響を考慮しないといけませんが、最終的な振動の式は同じになることが分かりました。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
