剛体振り子(Physical Pendulum)の運動方程式を求める方法を紹介します。
今回は、システムのエネルギーからラグランジュ方程式を用いた方法で運動方程式を算出します。
運動方程式をエネルギーからラグランジュ方程式を用いて求める方法は、こちらの記事を参考にしてください。
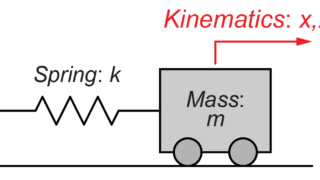
剛体振り子システム
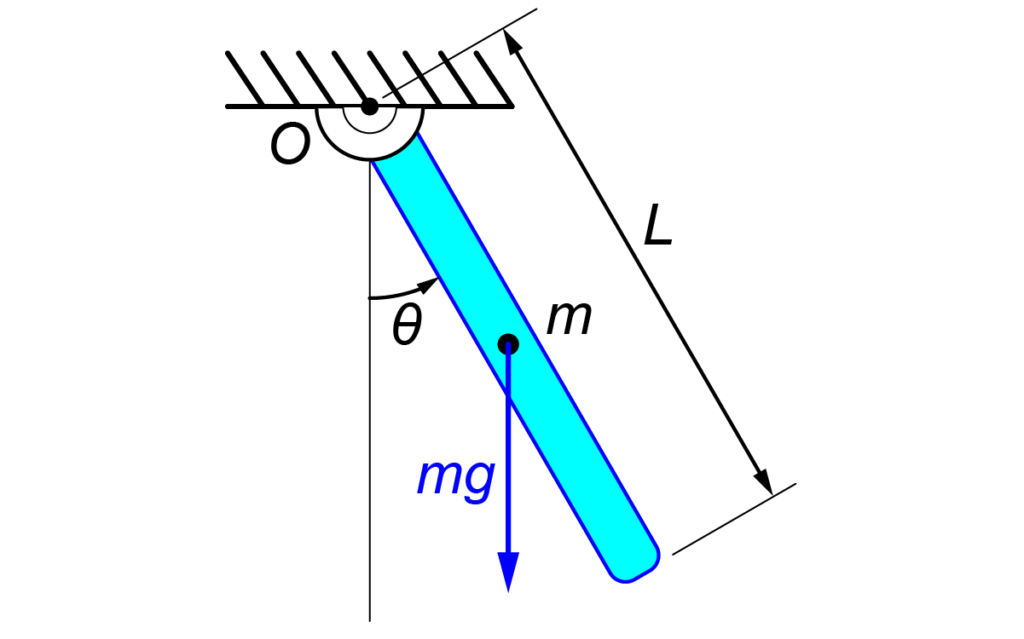
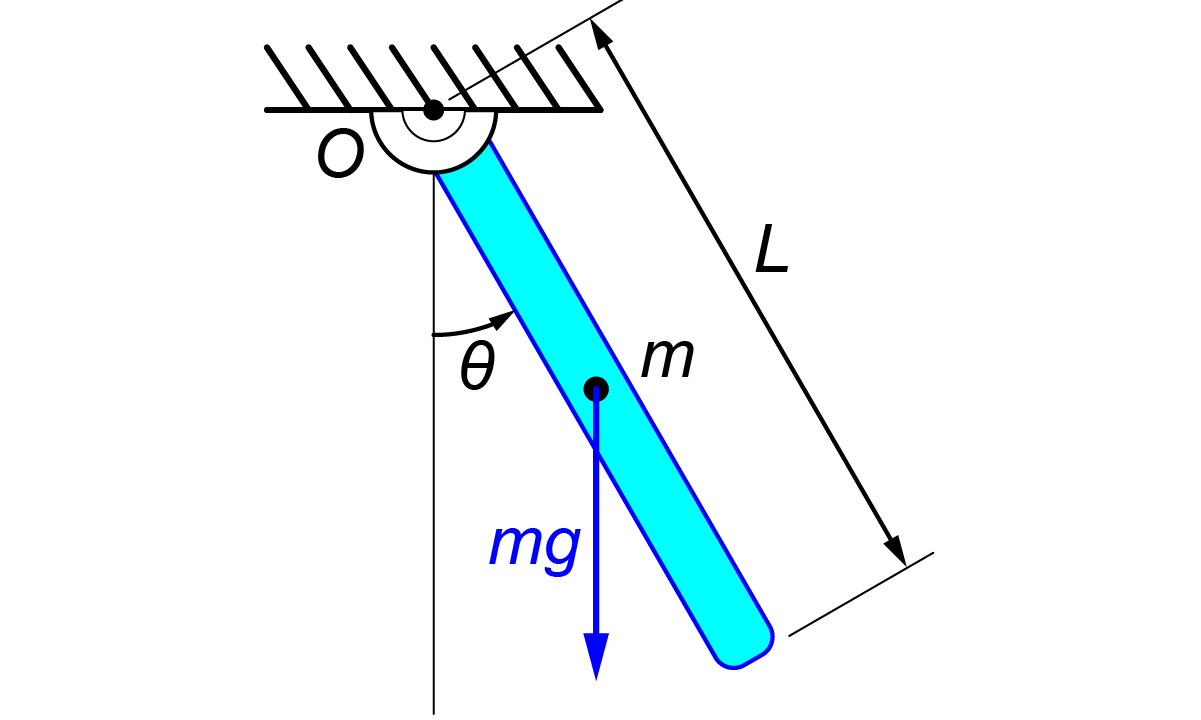
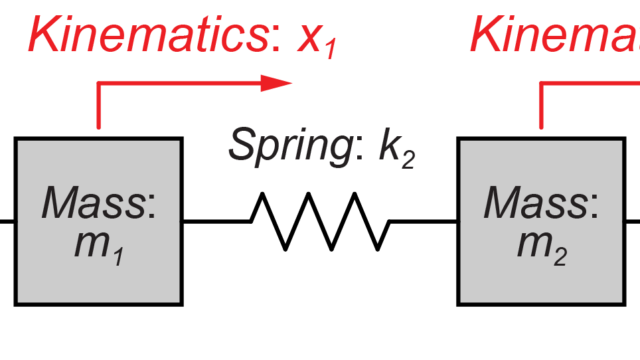
今回は図のような剛体による振り子について運動方程式を算出していきます。
長さL[m]、質量m[kg]の剛体が原点Oで天井に取り付けられています。
この時の垂線からの剛体の角度をθ[rad]、重力加速度をg[m/sec2]とした時の、このシステムの運動方程式を求めていきます。
ラグランジュ方程式から運動方程式の算出方法
ラグランジュ方程式を用いて運動方程式を求めていきます。
システムの運動エネルギーKEと位置エネルギーPEから運動方程式は、ラグランジュ方程式を用いて、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = 0$$
と表すことが出来ます。

運動エネルギーと位置エネルギー
運動方程式を求めるために、システムの運動エネルギー(KE)と位置エネルギー(PE)を算出していきます。
運動エネルギー
回転運動する物体の運動エネルギーKEは、慣性モーメントIと角速度\(\dot{\theta}\)(またはω)の2乗に比例します。
物体が端点oを中心に回転した場合の慣性モーメントIoは、
$$ I_o = \frac{1}{3} m L^2 $$
と表すことが出来ます。
よって、このシステムの運動エネルギーは、
$$ \begin{eqnarray} KE &=& \frac{1}{2} I_o \dot{\theta}^2 \\ &=& \frac{1}{2} \left[\frac{1}{3} m L^2 \right] \dot{\theta}^2 \end{eqnarray} $$
となります。
位置エネルギー
重力加速度gによる物体の位置エネルギーPEは、質量mと高さhに比例します。
今回の剛体振り子について、物体の角度がθの時の物体の重心の高さhは、角度θ=0を基準にすると、
$$ h = \frac{L}{2} \left( 1 – \cos (\theta) \right) $$
と表すことが出来ます。
よって、このシステムの位置エネルギーは、
$$ \begin{eqnarray} PE &=& m g h \\ &=& m g \frac{L}{2} \left( 1 – \cos (\theta) \right) \end{eqnarray} $$
となります。
システムの運動方程式を求める
算出した運動エネルギーと位置エネルギーをラグランジュ方程式から導いた式に代入すると、
$$ \begin{eqnarray} \begin{array}{l} \frac{d}{dt} \left( \frac{\partial}{\partial \dot{\theta}} KE \right) + \frac{\partial}{\partial \theta} PE = 0 \\ \Rightarrow \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} \left( \frac{1}{2} \left[\frac{1}{3} m L^2 \right] \dot{\theta}^2 \right) \right) + \frac{\partial}{\partial x} \left( m g \frac{L}{2} \left( 1 – \cos (\theta) \right) \right) = 0 \\ \Rightarrow \frac{d}{dt} \left( \frac{1}{3} m L^2 \dot{\theta} \right) + m g \frac{L}{2} \sin (\theta) = 0 \\ \Rightarrow \frac{1}{3} m L^2 \ddot{\theta} + \frac{L}{2} m g \sin (\theta) = 0 \end{array} \end{eqnarray} $$
とシステムの運動方程式を求めることが出来ます。
まとめ
今回は、運動エネルギーと位置エネルギーから剛体振り子システムの運動方程式を求める方法を紹介しました。
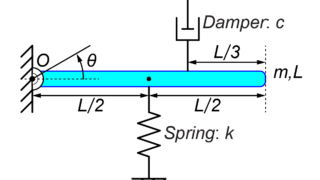
次回は少し複雑になった例として、ダンパーを含んだシステムについて運動方程式を求める方法を紹介したいと思います。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
