複数の質量からなるモデルを用いて、このシステムの振動を算出する方法を紹介します
前の記事では、2質量モデルの運動方程式を求める方法を紹介しました。
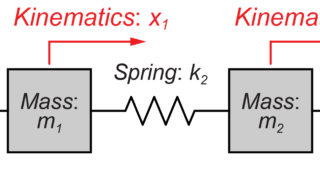
今回は、運動方程式からシステムの振動の様子をラプラス変換を用いて算出する方法を紹介します。
2質量モデルの運動方程式
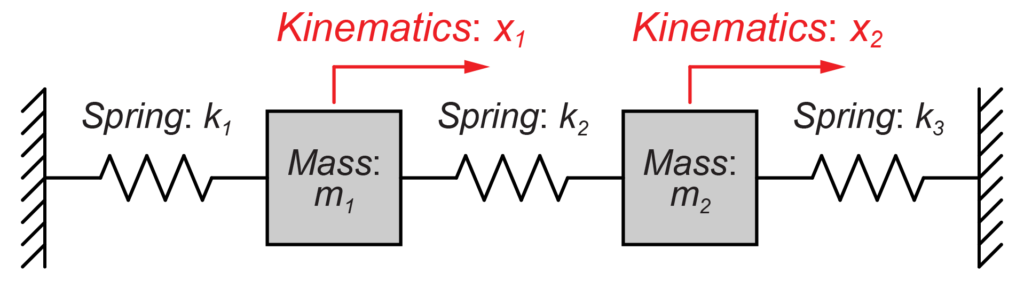
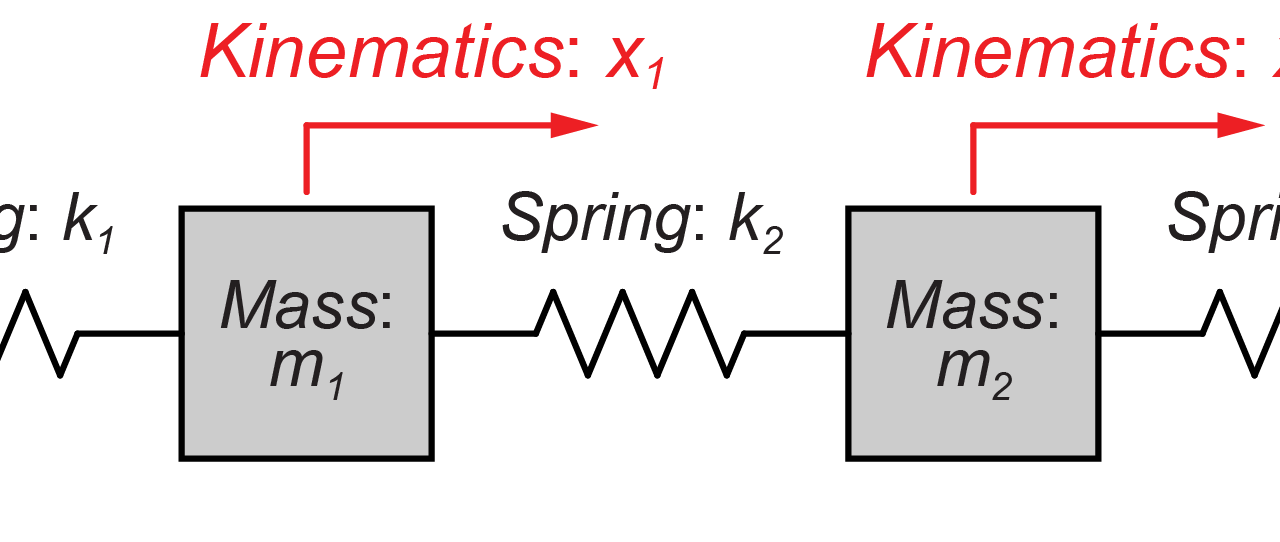
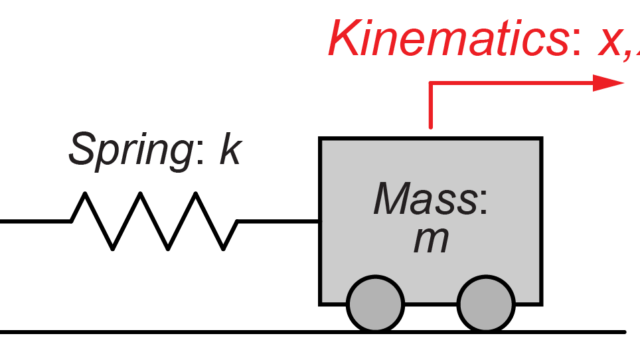
図のように2つの質量(m1とm2)が、それぞればね(k1、k2、k3)によって壁と互いに接続されているモデルを扱います。
この2質量モデルの運動方程式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left(k_1 + k_2\right) x_1(t) – k_2 x_2(t) = 0 \\ m_2 \ddot{x}_2(t) – k_2 x_1(t)+ \left(k_2 + k_3\right) x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
と表すことが出来ます。
詳しくは、こちらの記事を参考にしてください。

今回は問題の簡略化のため、
$$ m_1 = m_2 = m $$
$$ k_1 = k_2 = k_3 = k $$
として考えます。
この条件を基にシステムの運動方程式を書き換えると、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m \ddot{x}_1(t) + 2 k x_1(t) – k x_2(t) = 0 \\ m \ddot{x}_2(t) – k x_1(t) + 2 k x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
となります。
さらに初期条件として、時刻t=0において、
$$ x_1(0) = 0 $$
$$ x_2(0) = 1 $$
$$ \dot{x}_1(0) = \dot{x}_2(0) = 0 $$
とします。
この条件のもと、運動方程式に対してラプラス変換を行い、システムの振動の様子を算出していきます。
2質量モデルとラプラス変換
2質量モデルの運動方程式を
$$ \begin{eqnarray} \left\{ \begin{array}{l} m \ddot{x}_1(t) + 2 k x_1(t) – k x_2(t) = 0 \\ m \ddot{x}_2(t) – k x_1(t) + 2 k x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
$$ \Rightarrow \begin{eqnarray} \left\{ \begin{array}{l} \ddot{x}_1(t) + 2 {\omega_n}^2 x_1(t) – {\omega_n}^2 x_2(t) = 0 \\ \ddot{x}_2(t) – {\omega_n}^2 x_1(t) + 2 {\omega_n}^2 x_2(t) = 0 \end{array} \right. \end{eqnarray} $$
と一般的な式に置き換えます。
ここで、
$$ \omega_n = \sqrt{\frac{k}{m}} $$
です。
この2式をラプラス変換を用いて時間領域tから複素数領域sに変換すると、
$$ \begin{eqnarray} \left\{ \begin{array}{l} X_1(s) \left( s^2 + 2 {\omega_n}^2 \right) + X_2(s) \left(- {\omega_n}^2 \right) = 0 \\ X_1(s) \left(- {\omega_n}^2 \right) + X_2(s) \left( s^2 + 2 {\omega_n}^2 \right) = s \end{array} \right. \end{eqnarray} $$
となります。
この連立方程式をX1(s)とX2(s)について解いていきます。
まずX1(s)について解くと、
$$ X_1(s) = \frac{\mathrm{ det } \begin{vmatrix} 0 & – {\omega_n}^2 \\ s & s^2 + 2 {\omega_n}^2 \end{vmatrix}}{\mathrm{ det } \begin{vmatrix} s^2 + 2 {\omega_n}^2 & – {\omega_n}^2 \\ – {\omega_n}^2 & s^2 + 2 {\omega_n}^2 \end{vmatrix}} $$
$$ = \frac{{\omega_n}^2 s}{\left( s^2 + 2 {\omega_n}^2 \right)^2 – {\omega_n}^4} = \frac{{\omega_n}^2 s}{\left( s^2 + {\omega_n}^2 \right)^2 \left( s^2 + 3 {\omega_n}^2 \right)^2} $$
$$ = \frac{\frac{1}{2} s}{s^2 + {\omega_n}^2} + \frac{-\frac{1}{2} s}{s^2 + 3 {\omega_n}^2} $$
となります。
このX1(s)を逆ラプラス変換を用いて複素数領域sから時間領域tに変換すると,
$$ x_1(t) = \frac{1}{2} \cos \left( \omega_n t \right) – \frac{1}{2} \cos \left( \sqrt{3} \omega_n t \right) $$
となり、質量m1についての運動x1(t)を式で表すことが出来ます。
同様に、X2(s)について解いたものを逆ラプラス変換すると、
$$ x_2(t) = \frac{1}{2} \cos \left( \omega_n t \right) + \frac{1}{2} \cos \left( \sqrt{3} \omega_n t \right) $$
と質量m2についての運動x2(t)を式で表すことが出来ました。
まとめ
今回は、2質量モデルの運動方程式からシステムの振動の様子をラプラス変換を用いて算出する方法を紹介しました。
システム内に複数の質量が含まれる場合でも、1質量の場合と同様の手法で解くことが出来ます。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
