入力に対するシステムの応答を算出する

ラプラス変換を用いて、力が与えられた時の質量-ばね-ダンパーシステムの応答を求めていきます。

今回は、入力する力に対する応答の種類として、

• インパルス応答
• ステップ応答

について考えていきます。

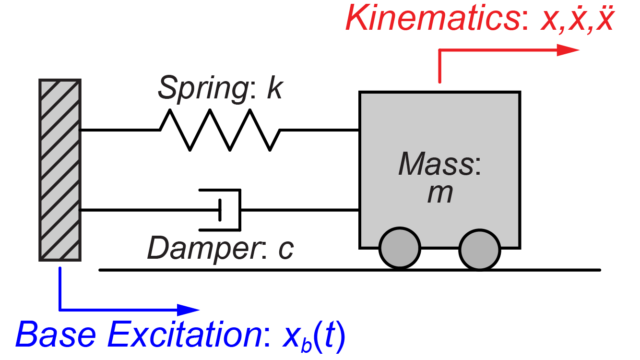
質量-ばね-ダンパーモデル

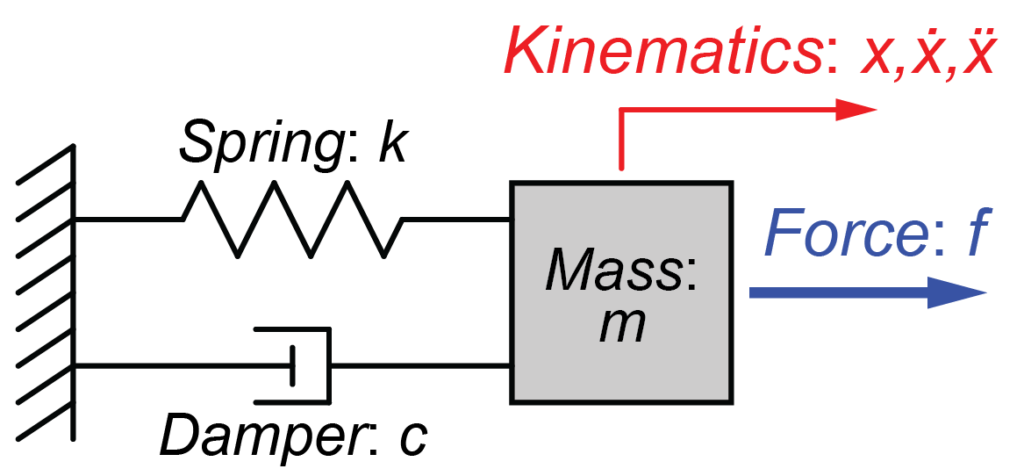
図のように質量\(m\)がばね\(k\)とダンパー\(c\)で壁に接続されているモデルを扱います。

このモデルに力\(f(t)\)が与えられた時の運動方程式は、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t)$$

となります。

運藤方程式の導出についての詳細は、こちらの記事を参考にしてください。

入力ありの質量-ばね-ダンパーモデルの運動を求める 今回は、質量-ばね-ダンパーモデルを用いて、入力として力が質量に与えられている場合のシステムの運動を考えます。 入...

このモデルの質量\(m\)に力\(f(t)\)が与えられた時のシステムの応答（質量の変位：\(x(t)\)）を算出していきます。

二次系システム

質量-ばね-ダンパーモデルは、一般的に二次系システムと言われます。

２次系システムの運動方程式は、

$$ \ddot{x}(t) + 2 \zeta \omega_n \dot{x}(t) + \omega_n^2 x(t) = F(t)$$

と表すことが出来ます。

このように、運動方程式が線形2階微分の形になっているシステムが2次系システムです。

ここで、今回の質量-ばね-ダンパーモデルの運動方程式を、二次系システムの運動方程式の形に置き換えると、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t)$$

$$ \Rightarrow \ddot{x}(t) + \frac{c}{m} \dot{x}(t) + \frac{k}{m} x(t) = \frac{f(t)}{m} $$

となります。

これより、二次系システムの運動方程式の各変数（\(\omega_n\)と\(\zeta\)）は両式の係数の関係より、

$$ \omega_n^2 =  \frac{k}{m} $$

$$ \Rightarrow \omega_n = \sqrt{ \frac{k}{m} } $$

$$ 2 \zeta \omega_n = \frac{c}{m} $$

$$ \Rightarrow \zeta = \frac{1}{2 \omega_n} \frac{c}{m} = \frac{c}{2 \sqrt{k m}} $$

と算出する出来ることが分かります。

各変数（\(\omega_n\)、\(\zeta\)）の意味

求めた\(\omega_n\)と\(\zeta\)について、物理的な意味を説明していきます。

固有角振動数：\(\omega_n\)

\(\omega_n\)は固有角振動数（または固有角周波数、Natural Angular Frequency）と言われます。

物体を自由に振動させた時、その振動する物体の固有の角振動数（角周波数）を示します。

この固有角振動数\(\omega_n\)の値が高いほど物体の振動の周波数が高く（周期は短く）なります。

今回のモデルの例、

$$ \omega_n =  \sqrt{ \frac{k}{m} } $$

を用いると、ばね定数\(k\)が大きくなったり、質量\(m\)が小さくなると、より高い周波数でシステムが振動するようになることが分かります。

反対に、ばね定数\(k\)が小さくなったり、質量\(m\)が大きくなると、より低い周波数でシステムがゆっくりと振動することが分かります。

減衰比：\(\zeta\)

\(\zeta\)は減衰比（Damping Ratio）と言われます。

システム内の物体に力を加えた時、その物体が振動するかどうかを示します。

この減衰比\(\zeta\)の値が1またはそれ以上の場合は、システムは振動しません。

反対に減衰比\(\zeta\)の値が1より小さい場合はシステムは振動します。

今回のモデルの例、

$$ \zeta = \frac{c}{2 \sqrt{k m}} $$

を考えると、ばね定数\(k\)とダンパー係数\(c\)、質量\(m\)の組み合わせで決定していることが分かります。

一般的にダンパー係数\(c\)を調整して振動を制御することが多いと思います。

他のばね定数\(k\)を触ってしまうと振動の周波数も変わってしまいますし、質量\(m\)は変更できないことが多いからです。

この減衰比\(\zeta\)の値が\(\zeta=1\)の時のダンパー係数を臨界減衰係数（Critical Damping Coefficient、\(c_{cr}\)）と言われます。

まとめ

今回は、質量-ばね-ダンパーモデルに力が与えられた時のシステムの応答（質量の変位）を算出するために、基本的な二次系システムの運藤方程式の紹介をしました。

次回は、今回求めたモデルの運動方程式を用いて、実際に入力が与えられた時のシステムの応答を求めていきたいと思います。

インパルス入力に対するシステムの応答を算出する ラプラス変換を用いて、システムに外から力が与えられた時の質量-ばね-ダンパーシステムの応答を求めていきます。 前回...