ロボット工学において、順運動学や逆運動学を理解することはロボットや機械を制御する際にとても重要です。
以前の記事では、順運動学と逆運動学についての基本知識と簡単なモデルでの各運動学の算出結果を紹介しました。

前回の記事では、2リンクモデルの運動学のうち順運動学の式を求める方法を紹介しました。
今回の記事では、残りの2リンクモデルにおける逆運動学を求める方法を紹介したいと思います。
2リンクモデルと順運動学
前回のおさらいです。
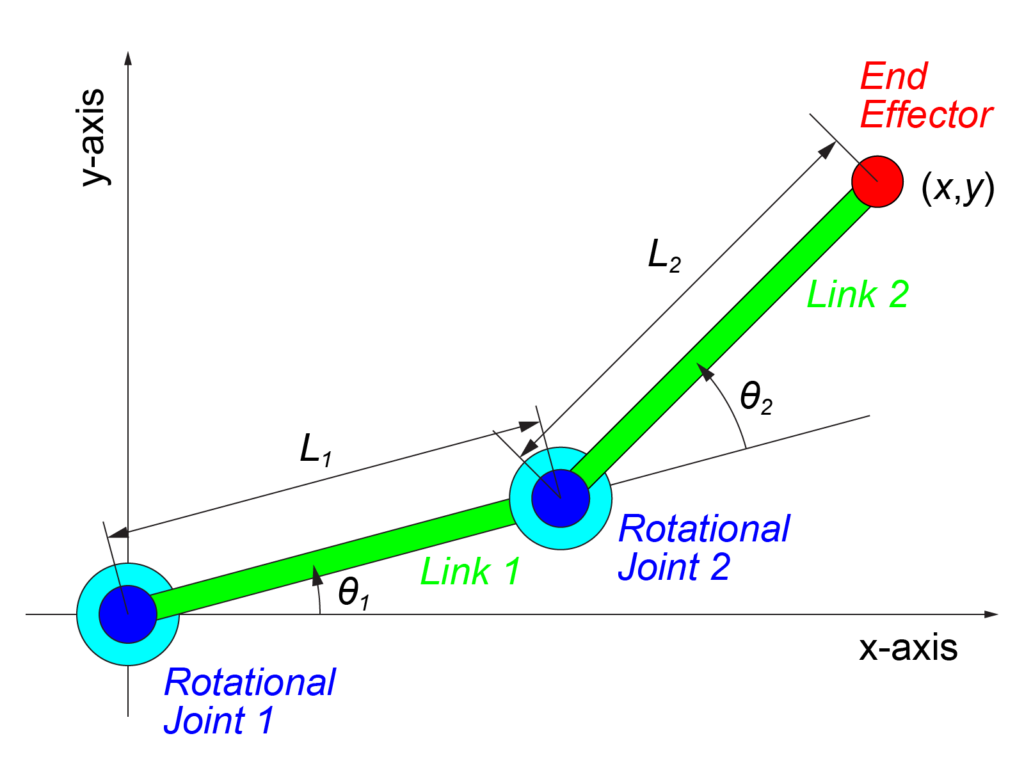
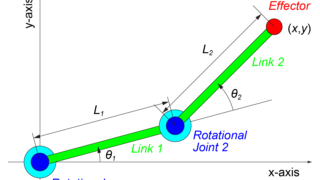
今回の記事では、上図のような2つの回転関節(Rotational Joint)と2つのリンク(Link)による2リンクモデルを取り扱います。
この2リンクモデルの順運動学は
$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$
の式で表されます。
2リンクモデルにおける順運動学の詳細は、こちらの記事を参考にしてください。

逆運動学の算出
では、2リンクモデルの逆運動学を求めていきます。
今回の記事では、逆運動学の式を求めるために、前回の記事で求めた順運動学の式を変換することで、ロボットの位置xとyから関節の変位θ1とθ2を表す数式を求めていきます。
この逆運動学の算出方法にも色々な手法がありますが、今回の記事ではθ1を求めた後に、そのθ1の値にあったθ2を求める流れで逆運動学の式を算出していきたいと思います。
θ1について求める
まず、順運動学の式を下のように移項して変換します。
$$ \begin{eqnarray} \left\{ \begin{array}{l} x &=& L_1 \cos \left( \theta_1 \right) + L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y &=& L_1 \sin \left( \theta_1 \right) + L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \\ \Rightarrow \left\{ \begin{array}{l} x – L_1 \cos \left( \theta_1 \right) &=& L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y – L_1 \sin \left( \theta_1 \right) &=& L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$
つぎに、この変換した2つの式の両辺を2乗します。
$$ \begin{eqnarray} \left\{ \begin{array}{l} x^2 – 2 x L_1 \cos \left( \theta_1 \right) + {L_1}^2 \cos^2 \left( \theta_1 \right) &=& {L_2}^2 \cos^2 \left( \theta_1 + \theta_2 \right) \\ y – 2 y L_1 \sin \left( \theta_1 \right) + {L_1}^2 \sin^2 \left( \theta_1 \right) &=& {L_2}^2 \sin^2 \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$
そして、2つの式の左辺と右辺をそれぞれ足し合わせることで、1つの式に変換します。
$$ \begin{eqnarray} x^2 + y^2 – 2 x L_1 \cos \left( \theta_1 \right) – 2 y L_1 \sin \left( \theta_1 \right) + {L_1}^2 \cos^2 \left( \theta_1 \right) + {L_1}^2 \sin^2 \left( \theta_1 \right) && \\ = {L_2}^2 \cos^2 \left( \theta_1 + \theta_2 \right) + {L_2}^2 \sin^2 \left( \theta_1 + \theta_2 \right) && \\ x^2 + y^2 – 2 L_1 \left( x \cos \left( \theta_1 \right) + y \sin \left( \theta_1 \right) \right) + {L_1}^2 \left( \cos^2 \left( \theta_1 \right) + \sin^2 \left( \theta_1 \right) \right) && \\ = {L_2}^2 \left( \cos^2 \left( \theta_1 + \theta_2 \right) + \sin^2 \left( \theta_1 + \theta_2 \right) \right) && \\ x^2 + y^2 – 2 L_1 \left( x \cos \left( \theta_1 \right) + y \sin \left( \theta_1 \right) \right) + {L_1}^2 = {L_2}^2 && \end{eqnarray} $$
その結果、θ1のみを含む式に変形することが出来ました。
この式をθ1について解くことで、逆運動学の式の1つを求められます。
θ1を含む項を左辺にまとめると、
$$ \begin{eqnarray} 2 L_1 \left( x \cos \left( \theta_1 \right) + y \sin \left( \theta_1 \right) \right) &=& x^2 + y^2 + {L_1}^2 – {L_2}^2 \\ x \cos \left( \theta_1 \right) + y \sin \left( \theta_1 \right) &=& \frac{x^2 + y^2 + {L_1}^2 – {L_2}^2}{2 L_1} \end{eqnarray} $$
となります。
ここで、三角関数における
$$ \begin{eqnarray} a \cos x + b \sin x = R \cos \left( x – \alpha \right) \\ where \ \left\{ \begin{array}{l} R = \sqrt{a^2+b^2} \\ \alpha = \tan^{-1} \left( \frac{b}{a} \right) \end{array} \right. \end{eqnarray}$$
という関係を用いると、先ほどの式の左辺は
$$ \sqrt{x^2+y^2} \cos \left( \theta_1 – \tan^{-1} \left( \frac{y}{x} \right) \right) = \frac{x^2 + y^2 + {L_1}^2 – {L_2}^2}{2 L_1} $$
と変換することが出来ます。
この式をθ1について解くと
$$ \begin{eqnarray} \cos \left( \theta_1 – \tan^{-1} \left( \frac{y}{x} \right) \right) &=& \frac{x^2 + y^2 + {L_1}^2 – {L_2}^2}{2 L_1 \sqrt{x^2+y^2}} \\ \theta_1 – \tan^{-1} \left( \frac{y}{x} \right) &=& \pm \cos^{-1} \left( \frac{x^2 + y^2 + {L_1}^2 – {L_2}^2}{2 L_1 \sqrt{x^2+y^2}} \right) \\ \theta_1 &=& \pm \cos^{-1} \left( \frac{x^2 + y^2 + {L_1}^2 – {L_2}^2}{2 L_1 \sqrt{x^2+y^2}} \right) + \tan^{-1} \left( \frac{y}{x} \right) \end{eqnarray} $$
となり、θ1に関する逆運動学の式を求めることが出来ました。
θ2について求める
同様に、残りのθ2についての逆運動学の式を求めていきます。
まず、θ1を求める際に変形した順運動学の式
$$ \begin{eqnarray} \left\{ \begin{array}{l} x – L_1 \cos \left( \theta_1 \right) &=& L_2 \cos \left( \theta_1 + \theta_2 \right) \\ y – L_1 \sin \left( \theta_1 \right) &=& L_2 \sin \left( \theta_1 + \theta_2 \right) \end{array} \right. \end{eqnarray} $$
について、2つ目の式を1つ目の式で割ると
$$ \frac{ y – L_1 \sin \left( \theta_1 \right) }{ x – L_1 \cos \left( \theta_1 \right) } = \frac{ L_2 \sin \left( \theta_1 + \theta_2 \right) }{ L_2 \cos \left( \theta_1 + \theta_2 \right) } $$
という関係式が導かれます。
ここで、右辺について
$$ \frac{ L_2 \sin \left( \theta_1 + \theta_2 \right) }{ L_2 \cos \left( \theta_1 + \theta_2 \right) } = \tan \left( \theta_1 + \theta_2 \right) $$
という変換を行うと、先ほどの式は
$$ \tan \left( \theta_1 + \theta_2 \right) = \frac{ y – L_1 \sin \left( \theta_1 \right) }{ x – L_1 \cos \left( \theta_1 \right) } $$
となります。
この式をθ2について解くと
$$ \begin{eqnarray} \tan \left( \theta_1 + \theta_2 \right) &=& \frac{ y – L_1 \sin \left( \theta_1 \right) }{ x – L_1 \cos \left( \theta_1 \right) } \\ \theta_1 + \theta_2 &=& \tan^{-1} \left( \frac{ y – L_1 \sin \left( \theta_1 \right) }{ x – L_1 \cos \left( \theta_1 \right) } \right) \\ \theta_2 &=& \tan^{-1} \left( \frac{ y – L_1 \sin \left( \theta_1 \right) }{ x – L_1 \cos \left( \theta_1 \right) } \right) – \theta_1 \end{eqnarray} $$
のように、θ2に関する逆運動学の式を求めることが出来ました。
逆運動学と複数解
取り扱っている2リンクモデルの「ロボットの位置(x、y)」から「関節の変位(θ1、θ2)」を求めるための逆運動学の式は
$$ \begin{eqnarray} \left\{ \begin{array}{l} \theta_1 &=& \pm \cos^{-1} \left( \frac{x^2 + y^2 + {L_1}^2 – {L_2}^2}{2 L_1 \sqrt{x^2+y^2}} \right) + \tan^{-1} \left( \frac{y}{x} \right) \\ \theta_2 &=& \tan^{-1} \left( \frac{ y – L_1 \sin \left( \theta_1 \right) }{ x – L_1 \cos \left( \theta_1 \right) } \right) – \theta_1 \end{array} \right. \end{eqnarray} $$
で表されることが分かりました。
ここで、算出した逆運動学のθ2の式にはθ1が含まれていることが分かります。
もちろん、θ1のみで表されているθ1の式と同様に、θ2の式もθ2のみで表すことは可能です。
しかし、今回紹介した逆運動学の式ではθ1を含んだ形としています。
これは、逆運動学には複数の解が存在する場合があるためです。
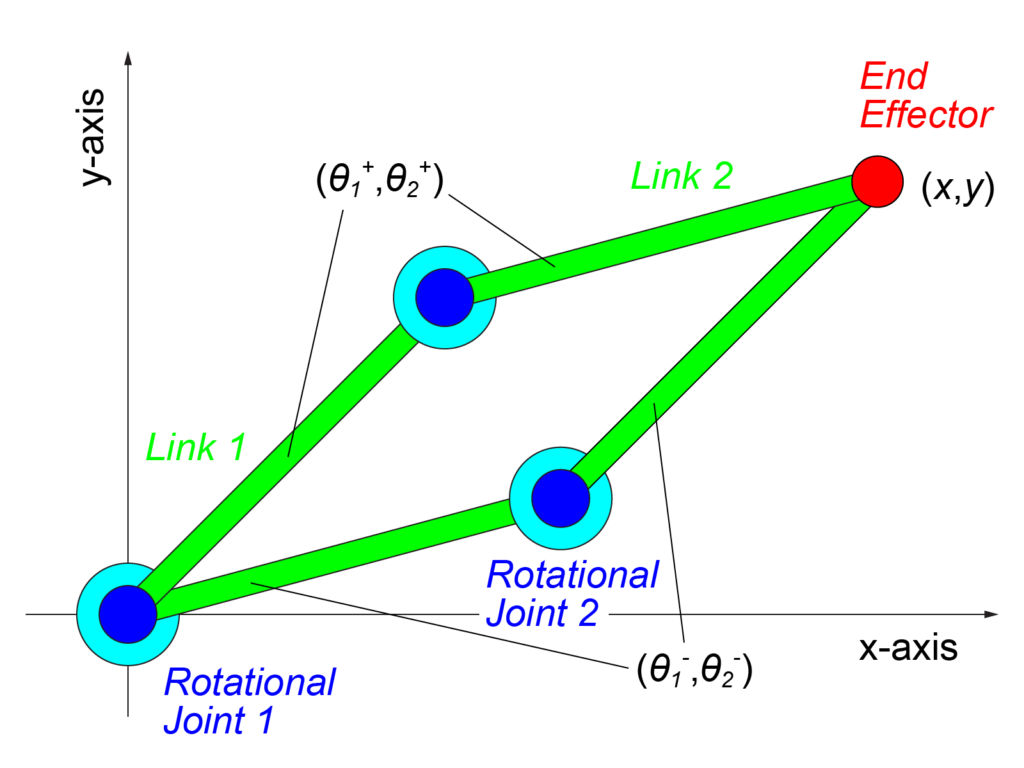
θ1の式を見ても分かるように、式に含まれるプラスとマイナスで2つの解があります。
そして、それぞれのθ1に対応するようにθ2も決定する必要があるため、θ2の式はθ1が含まれる形にしています。
そのため、もしθ2の式をθ1を含まずに求める場合は、反対にθ1の式をθ2を含んで表す必要があります。
まとめ
今回の記事では、2リンクモデルの運動学のうち逆運動学の式を求める方法を紹介しました。
前回の記事で求めた順運動学の式を変換することで、逆運動学の式を求めることが出来ることが分かりました。
前回で求めた順運動学の式と今回で求めた逆運動学の式で構成される運動学を用いることで、2リンクモデルの制御を行うことが出来ます。
合わせて読みたい
2リンクモデルの順運動学を求める方法について

運動学(順運動学と逆運動学)の基本について
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
