基礎励振（Base Excitation）モデルの運動方程式を算出する

基礎励振（Base Excitation）モデルについて、運動方程式を求める方法を説明したいと思います。

基礎励振（Base Excitation）モデル

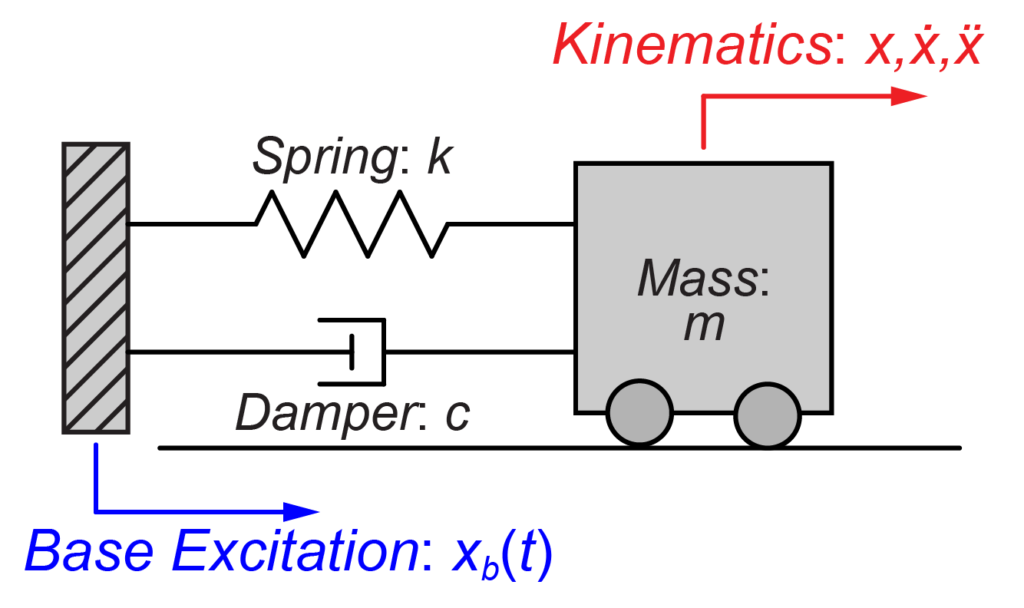
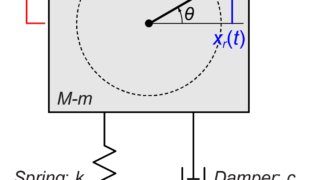
今回は基礎励振（Base Excitation）モデルとして、図のように質量mがばねkとダンパーcで壁に接続されている質量-ばね-ダンパーモデルを扱います。

今回のモデルでは、この壁が時刻tによって振動します。

（固定されていません。）

よって、入力として質量mに力Fが働いてない場合でも、壁の振動によって質量mも振動させられます。

この振動（運動）の様子をシステムの運動方程式から求めていきたいと思います。

基礎励振モデルの運動方程式

質量mまわりの力Fの合計は、質量mとその加速度a=\(\ddot{x}\)の積と同等になります。

$$ m a = \Sigma F $$

質量mにかかるばねkによる力F_sとダンパーcによる力F_dは、質量mの変位と速度（x(t)と\(\dot{x}\)(t)）と壁の変位と速度（x_b(t)と\(\dot{x}_b\)(t)）を用いて、

$$ F_s = – k \left( x(t) – x_b(t) \right) $$

$$ F_d = – c \left( \dot{x}(t) – \dot{x}_b(t) \right) $$

と計算出来ます。

よって、このシステムの運動方程式は、

$$ m \ddot{x}(t) = – c \left( \dot{x}(t) – \dot{x}_b(t) \right) – k \left( x(t) – x_b(t) \right) $$

より、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = c \dot{x}_b(t) + k x_b(t) $$

と表すことが出来ます。

この線形微分方程式を解くことで、壁が時刻tでx_b(t)と振動した際におけるシステムの運動を算出することが出来ます。

モデルの最大振幅

今回のような基礎励振モデルを用いて、色々な問題を解くことが出来ます。

例えば、車や飛行機などの乗り物が凸凹している地面を走る際に、どれぐらい車体が揺れるかを求めることが出来ます。

実際に地面の凹凸がx_b(t)=sin(ωt)とした時の車体の揺れについて計算してみます。

車体の振動の算出には、先ほど求めた基礎励振モデルの運動方程式をそのまま用います。

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = c \dot{x}_b(t) + k x_b(t) $$

壁がx_b(t)で振動した時の車体の運動を

$$ x(t) = K_1 \sin(\omega t) + K_2 \cos(\omega t) $$

として、x(t)をx_b(t)運動方程式に代入すると、

$$ m \left(- K_1 \omega^2 \sin(\omega t) – K_2 \omega^2 \cos(\omega t) \right)$$

$$+ c \left(K_1 \omega \cos(\omega t) – K_2 \omega \sin(\omega t) \right) $$

$$+ k \left( K_1 \sin(\omega t) + K_2 \cos(\omega t) \right) $$

$$= c \left( X_b \omega \cos(\omega t) \right) + k \left( X_b \sin(\omega t) \right) $$

となります。

これより、

$$ \begin{bmatrix} k – m \omega^2 & -c \omega \\ c \omega & k – m \omega^2 \end{bmatrix} \begin{bmatrix} K_1 \\ K_2 \end{bmatrix} = \begin{bmatrix} k X_b \\ c X_b \omega \end{bmatrix} $$

という関係式を導くことが出来ます。

この関係式をK₁とK₂について解くと、

$$ K_1 = \frac{k \left( k – m \omega^2 \right) + \left( c \omega \right)^2}{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2} X_b$$

$$ K_2 = \frac{- k c \omega + c \omega \left( k – m \omega^2 \right)}{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2} X_b$$

となります。

よって、質量mの運動x(t)の振幅の絶対値|X|は、

$$ |X| = \sqrt{K_1^2+K_2^2} $$

$$ = \frac{sqrt{k^2 + \left( c \omega \right)^2}}{\sqrt{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2}} |X_b| $$

と求めることが出来ます。

この式を用いることで、壁の振幅に対するシステムの振幅を算出することが出来ます。

まとめ

今回は、基礎励振（Base Excitation）モデルについて、運動方程式を求める方法とその応用例について紹介しました。

壁が動いていると、シンプルな固定壁に接続されている質量-ばね-ダンパーシステムに比べて複雑に見えますが、順を追って考えていくと意外と簡単にシステムの運動を求めることが出来たと思います。