前回は、ダンパーを含んだ剛体振り子の運動について加減衰システムとなる場合を説明しました。
今回は、残りの2つのケース
- 臨界減衰システム(Critically Damped System)
- 不足減衰システム(Underdamped System)
について説明したいと思います。
システムの運動方程式
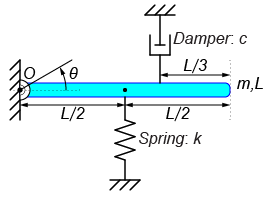
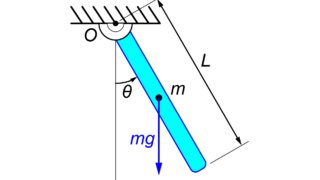
今回のモデルについて、棒の質量が\(m=1[kg]\)で長さが\(L=1[m]\)、そしてばね定数を\(k=10[N/m]\)とした時、
ケース1 ダンパーc=10[N/(m/s)] \(\leftarrow\)前回の記事
ケース2 ダンパーc=4.1079[N/(m/s)]
ケース3 ダンパーc=1[N/(m/s)]
での各ダンパー定数\(c\)の場合に、棒を時刻\(t=0\)で\(\theta_0=1[rad]\)で静かに離した時の運動を求めます。
このシステムの運動方程式は、
$$ \frac{1}{3} m L^2 \ddot{\theta} + \frac{4}{9} c L^2 \dot{\theta} + \frac{1}{4} k L^2 \theta = 0 $$
と表すことが出来ます。
この線形微分方程式を\(\theta\)について解き、各ケースでのパラメータを用いてシステムの運動を算出していきます。
実際にシステムの運動を求める
前回のケース1について求めた時と同様に、
ケース2 ダンパー\(c=4.1079[N/(m/s)]\)
ケース3 ダンパー\(c=1[N/(m/s)]\)
について、システムの運動を求めていきます。
ケース2: \(c=4.1079[N/(m/s)]\)
線形微分方程式について、この解を、
$$ \theta(t) = C_1 e^{\lambda_1 t} + C_2 e^{\lambda_2 t} $$
とした時の\(\lambda_1\)と\(\lambda_2\)を求めると、
$$ \lambda_{1,2} = – \frac{C}{2 M} \pm \frac{1}{2} \sqrt{\left( \frac{C}{M} \right)^2 – \frac{4 K}{M} } $$
となります。
これにケース2での各パラメータを入力すると、
$$ \lambda_1 = \lambda_2 = -2.7386 $$
となり、1つの同じ実数(\(\lambda_1=\lambda_2\))になることが分かります。
よって、このシステムの運動は、
$$ \theta(t) = C_1 e^{-2.7386 t} + C_2 t e^{-2.7386 t}$$
となります。
この式と時刻\(t=0\)での初期条件\(\theta(0)=\theta_0=1\)と\(\dot{\theta}(0)=0\)を用いて、\(C_1\)と\(C_2\)を求めます。
時刻\(t=0\)で\(\theta(0)=1\)なので、
$$ \theta(0) = C_1 e^{0} + C_2 \cdot 0 e^{0} = 1 $$
$$ \Rightarrow C_1 = 1 $$
の関係式が得られます。
次に、時刻\(t=0\)で\(\dot{\theta}(0)=0\)なので、
$$ \dot{\theta}(t) = -2.7386 C_1 e^{-2.7386 t} + C_2 e^{-2.7386 t}+ -2.7386 C_2 t e^{-2.7386 t}$$
$$ \Rightarrow \dot{\theta}(0) = -2.7386 C_1 e^{0} + C_2 e^{0} – 2.7386 C_2 \cdot 0 e^{0} = 0 $$
$$ \Rightarrow -2.7386 C_1 + C_2 = 0 $$
の関係式が得られます。
この2式を連立方程式として解くことで\(C_1\)と\(C_2\)は、
$$ C_1 = 1 $$
$$ C_2 = -2.7386 $$
となります。
よって、ケース2のパラメータでのシステムの運動は、
$$ \theta(t) =e^{ -2.7386 t} – 2.7386 t e^{ -2.7386 t}$$
と表すことが出来ます。
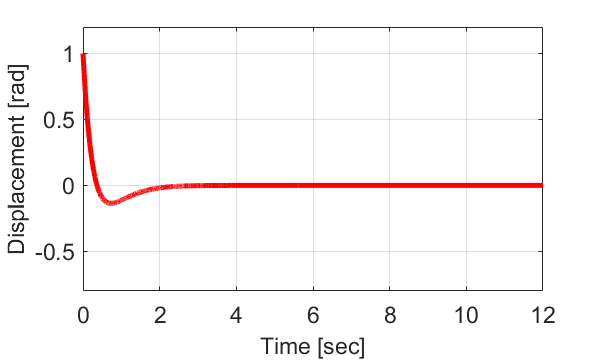
グラフで見ると、棒の角度が初期角度の\(\theta_0=1[rad]\)から徐々に小さくなり、一度少しだけ0超えたあと、また0に近づくことが分かります。
このようなシステムを臨界減衰システム(Critically Damped System)と言います。
ケース3: \(c=1[N/(m/s)]\)
ケース2と同様にケース3での各パラメータを入力すると、
$$ \lambda_1 = -0.6667 + 2.6562i $$
$$ \lambda_2 = -0.6667 – 2.6562i $$
となり、2つの同じ共役な複素数になることが分かります。
よって、このシステムの運動は、
$$ \theta(t) = C_1 e^{(-0.6667 + 2.6562i) t} + C_2 e^{(-0.6667 – 2.6562i) t}$$
となります。
このまま計算しても良いのですが、次のように式の形を変えて表したいと思います。
$$ \theta(t) = C_1 e^{(-0.6667 + 2.6562i) t} + C_2 e^{(-0.6667 – 2.6562i) t}$$
$$ = C_1 e^{-0.6667 t} e^{i 2.6562 t} + C_2 e^{-0.6667 t} e^{-i 2.6562 t} $$
$$ = e^{-0.6667 t} \left( C_1 e^{i 2.6562 t} + C_2 e^{-i 2.6562 t} \right) $$
$$ = e^{-0.6667 t} \left( A \cos (2.6562 t) + B \sin (2.6562 t) \right) $$
この式と時刻\(t=0\)での初期条件\(\theta(0)=\theta_0=1\)と\(\dot{\theta}(0)=0\)を用いて、\(A\)と\(B\)を求めます。
時刻\(t=0\)で\(\theta(0)=1\)なので、
$$ \theta(0) = e^{0} \left( A \cos (0) + B \sin (0) \right) = 1 $$
$$ \Rightarrow A = 1 $$
の関係式が得られます。
次に、時刻\(t=0\)で\(\dot{\theta}(0)=0\)なので、
$$ \dot{\theta}(t) = -0.6667 e^{-0.6667 t} \left( A \cos (2.6562 t) + B \sin (2.6562 t) \right) +e^{-0.6667 t} \left( -2.6562 A \sin (2.6562 t) + 2.6562 B \cos (2.6562 t) \right) $$
$$ \Rightarrow \dot{\theta}(0) = -0.6667 e^{0} \left( A \cos (0) + B \sin (0) \right) +e^{0} \left( -2.6562 A \sin (0) + 2.6562 B \cos (0) \right) = 0 $$
$$ \Rightarrow -0.6667 A + 2.6562 B = 0 $$
の関係式が得られます。
この2式を連立方程式として解くことで\(C_1\)と\(C_2\)は、
$$ A = 1 $$
$$ B = 0.2510 $$
となります。
よって、ケース3のパラメータでのシステムの運動は、
$$ \theta(t) =e^{-0.6667 t} \left( \cos (2.6562 t) + 0.2510 \sin (2.6562 t) \right) $$
と表すことが出来ます。
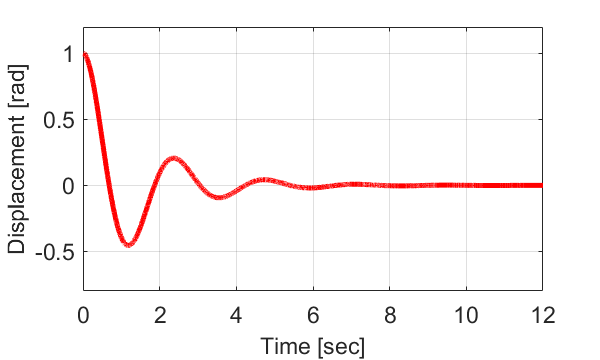
グラフで見ると、棒の角度が初期角度の\(\theta_0=1[rad]\)から振動しながら徐々に0に近づくことが分かります。
このようなシステムを不足減衰システム(Underdamped System)と言います。
まとめ
今回は、質量-ばね-ダンパーモデルを例に、実際に運動方程式からシステムの運動を求める方法を紹介しました。
今回の例では、臨界減衰システムと不足減衰システムとなる場合を取り扱い、システムの運動の様子を数式とグラフで表しました。




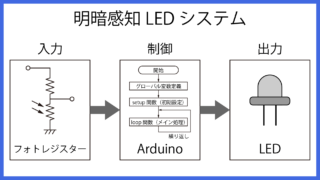
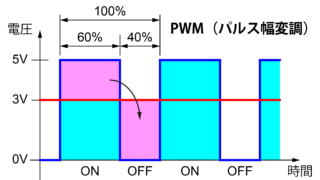
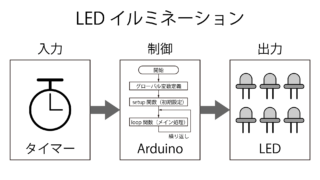
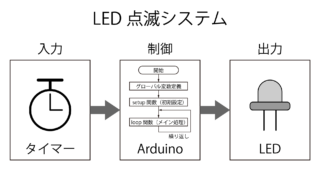
 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
