2質量モデルの振動を求める：運動方程式の算出

複数の質量からなるモデルを用いて、このシステムの振動を算出する方法を紹介します。

1つの質量からなるモデルの振動については、こちらの記事を参考にしてください。

質量-ばねシステムの振動を求める今回はシンプルな質量-ばねシステム（Mass Spring System）を用いて、このモデルの振動について算出していきたいと思...

Contents

2質量モデル
2質量モデルの各エネルギー
- 運動エネルギー
- 位置エネルギー
2質量モデルのラグランジュ方程式
- x₁について
- x₂について
2質量モデルの運動方程式
まとめ

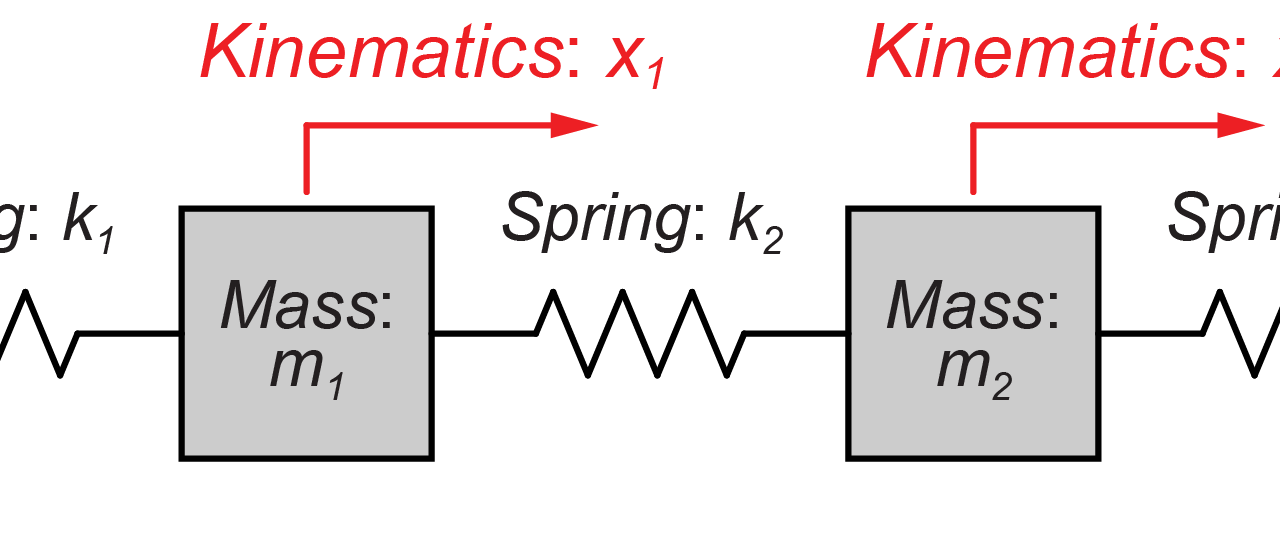
2質量モデル

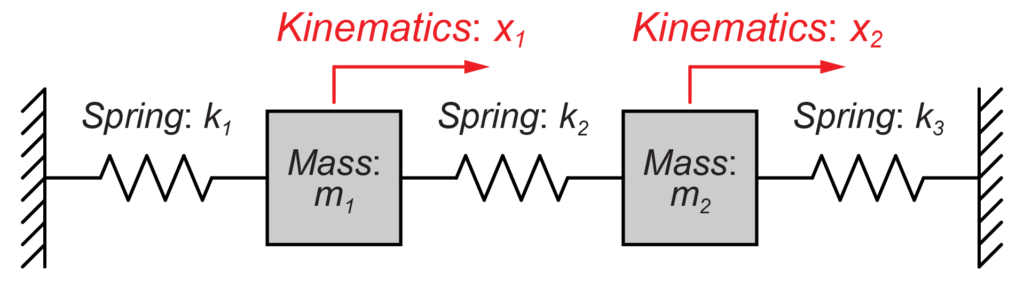
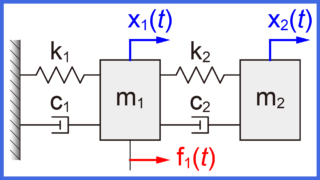
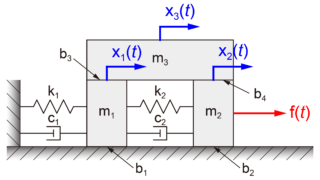
今回は、図のように2質量（m₁とm₂）がそれぞればね（k₁、k₂、k₃）によって壁と互いに接続されているモデルを扱います。

システム内に質量が２つありますが、質量が1つの場合と同様に、ラグランジュ方程式を用いて運動方程式を求めていきます。

2質量モデルの各エネルギー

ラグランジュ方程式を用いて運動方程式を求めるために、システムの運動エネルギーと位置エネルギーを求めていきます。

運動エネルギー

質量m₁の運動エネルギーKE₁は、質量m₁とその速度$\dot{x}_1$の2乗より、

$$ {KE}_1 = \frac{1}{2} m_1 {\dot{x}_1}^2 $$

と表すことが出来ます。

同様に、質量m₂の運動エネルギーKE₂は、質量m₂とその速度$\dot{x}_2$の2乗より、

$$ {KE}_2 = \frac{1}{2} m_2 {\dot{x}_2}^2 $$

と表すことが出来ます。

よって、システム全体の運動エネルギーKEは、2つの質量の運動エネルギーの計より、

$$ KE = {KE}_1 + {KE}_2 $$

$$ = \frac{1}{2} m_1 {\dot{x}_1}^2 + \frac{1}{2} m_2 {\dot{x}_2}^2 $$

となります。

位置エネルギー

位置エネルギーPEはシステム内のばね（k₁、k₂、k₃）による位置エネルギーの計で求めることが出来ます。

ばねk₁による位置エネルギーPE₁は、ばねk₁とその変位$x_1$の2乗より、

$$ {PE}_1 = \frac{1}{2} k_1 {x_1}^2 $$

と表すことが出来ます。

同様に、ばねk₃による位置エネルギーPE₃は、ばねk₃とその変位$x_2$の2乗より、

$$ {PE}_3 = \frac{1}{2} k_3 {x_2}^2 $$

と表すことが出来ます。

2質量間のばねk₂による位置エネルギーは、ばねk₂とその変位（x₂ – x₁）の2乗より、

$$ {PE}_2 = \frac{1}{2} k_2 \left(x_2 – x_1\right)^2 $$

となります。

よって、システム全体の位置エネルギーPEは、各位置エネルギーの計より、

$$ PE = {PE}_1 + {PE}_2 + {PE}_3 $$

$$ = \frac{1}{2} k_1 {x_1}^2 + \frac{1}{2} k_2 \left(x_2 – x_1\right)^2 + \frac{1}{2} k_3 {x_2}^2 $$

となります。

2質量モデルのラグランジュ方程式

複数の質量を含むモデルのラグランジュ方程式は、

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}_i} KE \right) + \frac{\partial}{\partial x_i} PE = 0$$

と表すことが出来ます。

今回のシステムにおけるx_iは、x₁とx₂です。

このラグランジュ方程式に各エネルギーの値を代入して解いていきます。

x₁について

各エネルギーをラグランジュ方程式に代入した関係式をx₁について解いていきます。

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}_1} \left(\frac{1}{2} m_1 {\dot{x}_1}^2 + \frac{1}{2} m_2 {\dot{x}_2}^2\right) \right) $$

$$ + \frac{\partial}{\partial x_1} \left(\frac{1}{2} k_1 {x_1}^2 + \frac{1}{2} k_2 \left(x_2 – x_1\right)^2 + \frac{1}{2} k_3 {x_2}^2\right) = 0$$

$$ \Rightarrow m_1 \ddot{x}_1(t) + k_1 x_1(t) – k_2 \left(x_2 – x_1\right) = 0 $$

よって、x₁についての運動方程式は、

$$ m_1 \ddot{x}_1(t) + \left(k_1 + k_2\right) x_1(t) – k_2 x_2(t) = 0 $$

となりました。

x₂について

同様に、各エネルギーをラグランジュ方程式に代入した関係式をx₂について解いていきます。

x₁について求めた時と同様に、x₂についての運動方程式は、

$$ m_2 \ddot{x}_2(t) – k_2 x_1(t)+ \left(k_2 + k_3\right) x_2(t) = 0 $$

となります。

2質量モデルの運動方程式

先程求めた2式から、今回の2質量モデルの運動方程式は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left(k_1 + k_2\right) x_1(t) – k_2 x_2(t) = 0 \\ m_2 \ddot{x}_2(t) – k_2 x_1(t)+ \left(k_2 + k_3\right) x_2(t) = 0 \end{array} \right. \end{eqnarray} $$

となりました。

この2式を行列式として1式にまとめると、

$$ \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix} \begin{bmatrix} \ddot{x_1} \\ \ddot{x_2} \end{bmatrix} + \begin{bmatrix} k_1+k_2 & -k_2 \\ -k_2 & k_2+k_3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$

と表すことが出来ます。