ヤコビ行列を使ってロボットの運動を計算する

今回はヤコビ行列について説明したいと思います。

ヤコビ行列を使うことで、ロボットの「関節の速度」と「手先の速度」の関係を示すことが出来ます。

ヤコビ行列とは

ロボット工学におけるヤコビ行列（ヤコビアン）とは、ロボットの各関節が微小変位した時の、ロボットの位置姿勢の微小変位を表すためのものです。

ヤコビ行列は、ロボットの順運動学の各式（\( f_i \)）について、各関節を変数（\( x_i \)）として微分することで求めることが出来ます。

$$ \boldsymbol{ J } = \begin{bmatrix} \frac{ \partial f_1 }{ \partial x_1 } & \frac{ \partial f_1 }{ \partial x_2 } \\ \frac{ \partial f_2 }{ \partial x_1 } &  \frac{ \partial f_2 }{ \partial x_2 } \end{bmatrix} $$

ヤコビ行列の計算

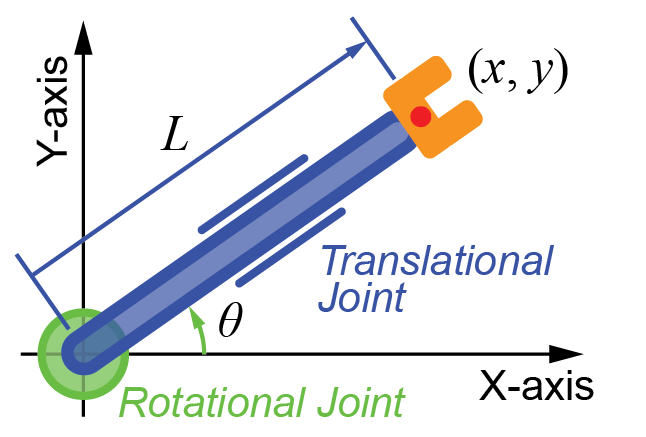
実際にシンプルなモデルを用いてヤコビ行列を計算していきます。

このモデルの順運動学は、下記のように表すことが出来ます。

$$ x = L \cos \theta $$

$$ y = L \sin \theta $$

詳しい算出方法は、こちらの記事を参考にしてください。

ロボット工学の基礎　順運動学と逆運動学を理解する ロボット工学を学ぶうえで必要な基本、 『順運動学』と『逆運動学』について解説してきます。 運動学の定義 運動学...

この順運動学の各式\( x, y \)について、各関節の変数\( L, \theta \)で微分していきます。

$$ \boldsymbol{ J } = \begin{bmatrix} \cos \theta & -L \sin \theta \\ \sin \theta &  L\cos \theta \end{bmatrix} $$

ヤコビ行列を使った速度の関係式

ヤコビ行列はロボットの関節の微小変位（\( \Delta q \)）と位置姿勢の微小変位（\( \Delta r \)）の関係を表すと説明してきました。

$$ \Delta r = \boldsymbol{ J } \Delta q $$

ここで、両辺を微小時間（\( \Delta t \)）で割ると、

$$ \frac{\Delta r}{\Delta t} = \boldsymbol{ J } \frac{\Delta q}{\Delta t} $$

となり、

$$ \dot{\Delta r} = \boldsymbol{ J } \dot{\Delta q} $$

というように速度の関係を示すことが出来ます。

まとめ

微分が必要なため計算が多少複雑なヤコビ行列ですが、関節の速度からロボットの速度を計算できるため、とても便利です。

またヤコビ行列の逆行列を用いることで、ロボットを目標の速度で動かすために必要な関節の速度を計算することもできます。

合わせて読みたい

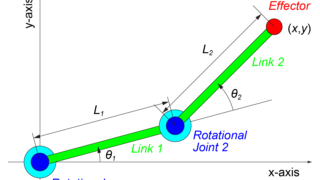
2リンクモデルのヤコビ行列について紹介しています。

2リンクモデルのヤコビ行列を算出する方法 ヤコビ行列を用いることで、ロボットの「関節の速度」と「手先の速度」の関係を示すことが出来ます。 https://tajim...