モード解析を使って2質量システムの運動を求める：その２

モード解析（Modal Analysis）を用いることで、システムがどのように振動するかを求めることが出来ます。

前回の記事では、2質量システムを例にモード解析の使って、振動の周波数と振幅を算出しました。

モード解析を使って2質量システムの運動を求める システムがどのように振動するかを求める方法にモード解析（Modal Analysis）があります。 2質量システム...

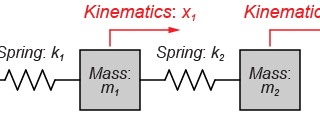
今回は、求めた振動の周波数と振幅を用いて、実際にシステムの振動を算出していきます。

2質量モデルとモード解析

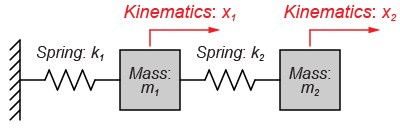
図のように2つの質量（\(m_1\)と\(m_2\)）が、それぞればね（\(k_1\)と\(k_2\)）によって壁と互いに接続されているモデルを扱います。

各パラメータについて、

$$ m_1 = m_2 = m $$

$$ k_1 = 3 k $$

$$ k_2 = 2 k $$

とすると、この2質量モデルの運動方程式は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} m \ddot{x}_1(t) + 5 k x_1(t) – 2 k x_2(t) = 0 \\ m \ddot{x}_2(t) – 2 k x_1(t) + 2 k x_2(t) = 0 \end{array} \right. \end{eqnarray} $$

となります。

このシステムについてモード解析を用いると、振動の周波数は、

$$ {\omega_1}^2 = 1 $$

$$ {\omega_2}^2 = 6 $$

となり、各周波数（\(\omega_1\)と\(\omega_2\)）に対する振幅（\(X_1\)と\(X_2\)）は、

$$ X_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix} $$

$$ X_2 = \begin{bmatrix} 1 \\ – \frac{1}{2} \end{bmatrix} $$

と表すことが出来ます。

詳しくはこちらの記事を参考にしてください。

モード解析を使って2質量システムの運動を求める システムがどのように振動するかを求める方法にモード解析（Modal Analysis）があります。 2質量システム...

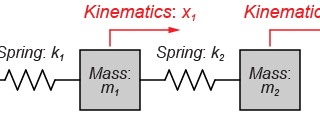
モード解析によって求めたパラメータを使って、初期条件として時刻\(t=0\)で

$$ x_1(0) = 1 $$

$$ x_2(0) = 0 $$

$$ \dot{x}_1(0) = \dot{x}_2(0) = 0 $$

とした時の2質量システムの運動を算出していきます。

2質量システムの振動を求める

システム内の各質量の運動（\(x_1(t)\)と\(x_2(t)\)）を

$$ x_1(t) = A_1^1 \sin \left( \omega_1 t – \phi_1 \right) + A_1^2 \sin \left( \omega_2 t – \phi_2 \right) $$

$$ x_2(t) = A_2^1 \sin \left( \omega_1 t – \phi_1 \right) + A_2^2 \sin \left( \omega_2 t – \phi_2 \right) $$

と置いて、式の中に含まれるパラメータ（振幅、周波数、位相）を求めていきます。

振幅の関係を求める

モード解析で求めた振幅の関係

$$ X_1 = \begin{bmatrix} 1 \\ 2 \end{bmatrix} $$

$$ X_2 = \begin{bmatrix} 1 \\ – \frac{1}{2} \end{bmatrix} $$

を用いて、

$$ A_2^1 = \frac{1}{2} A_1^1 $$

$$ A_2^2 = – 2 A_1^2 $$

と求めることが出来ます。

この関係式を各質量の運動の式に代入すると、

$$ x_1(t) = A_1^1 \sin \left( \omega_1 t – \phi_1 \right) + A_1^2 \sin \left( \omega_2 t – \phi_2 \right) $$

$$ x_2(t) = \frac{1}{2} A_1^1 \sin \left( \omega_1 t – \phi_1 \right) – 2 A_1^2 \sin \left( \omega_2 t – \phi_2 \right) $$

となります。

初期条件を用いる

初期条件を用いて位相\(\phi_i\)と振幅\(A_i^j\)を求めていきます。

時刻\(t=0\)で\(x_1(0)=1\)かつ\(x_2(0)=0\)なので、

$$ x_1(t) = A_1^1 \sin \left( – \phi_1 \right) + A_1^2 \sin \left( – \phi_2 \right) = 1 $$

$$ x_2(t) = \frac{1}{2} A_1^1 \sin \left( – \phi_1 \right) – 2 A_1^2 \sin \left( – \phi_2 \right) = 0$$

となります。

同様に、速度\(\dot{x}_1(t)と\dot{x}_2(t)\)について、

$$ \dot{x}_1(t) = \omega_1 A_1^1 \cos \left( \omega_1 t – \phi_1 \right) + \omega_2 A_1^2 \cos \left( \omega_2 t – \phi_2 \right) $$

$$ \dot{x}_2(t) = \frac{1}{2} \omega_1 A_1^1 \cos \left( \omega_1 t – \phi_1 \right) – 2 \omega_2 A_1^2 \cos \left( \omega_2 t – \phi_2 \right) $$

となり、時刻\(t=0\)で\(\dot{x}_1(0)=\dot{x}_2(0)=0\)なので、

$$ \dot{x}_1(t) = \omega_1 A_1^1 \cos \left(- \phi_1 \right) + \omega_2 A_1^2 \cos \left(- \phi_2 \right) = 0 $$

$$ \dot{x}_2(t) = \frac{1}{2} \omega_1 A_1^1 \cos \left(- \phi_1 \right) – 2 \omega_2 A_1^2 \cos \left( – \phi_2 \right) = 0 $$

となります。

ここで、振幅\(A_i^j\)及び周波数\(\omega_i\)が0ではないとすると、位相\(\phi_i\)は2式の関係式より、

$$ \phi_1 = -\frac{\pi}{2} $$

$$ \phi_2 = -\frac{\pi}{2} $$

となります。

求めた位相\(\phi_i\)を時刻\(t=0\)での位置（変位）の式に代入すると、

$$ x_1(t) = A_1^1 \sin \left( \frac{\pi}{2} \right) + A_1^2 \sin \left( \frac{\pi}{2} \right) = A_1^1 + A_1^2 = 1 $$

$$ x_2(t) = \frac{1}{2} A_1^1 \sin \left( \frac{\pi}{2} \right)  – 2 A_1^2 \sin \left(\frac{\pi}{2} \right) = \frac{1}{2} A_1^1  – 2 A_1^2 = 0 $$

となります。

これを連立方程式として解くと、振幅\(A_1^1\)と\(A_1^2\)は

$$ A_1^1 = \frac{4}{5} $$

$$ A_1^2 = \frac{1}{5} $$

となります。

これより、振幅\(A_2^1\)と\(A_2^2\)は

$$ A_2^1 = \frac{1}{2} A_1^1 = \frac{2}{5} $$

$$ A_2^2 = – 2 A_1^2 = – \frac{2}{5} $$

と求めることが出来ます。

よって、2質量システムの運動は、

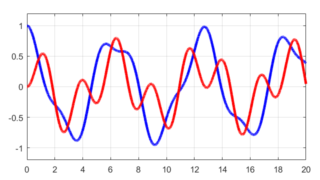
$$ x_1(t) = \frac{4}{5} \sin \left( t + \frac{\pi}{2} \right) +\frac{1}{5}\sin \left( \sqrt{6} t + \frac{\pi}{2} \right) $$

$$ x_2(t) = \frac{2}{5} \sin \left( t + \frac{\pi}{2} \right) – \frac{2}{5} \sin \left( \sqrt{6} t + \frac{\pi}{2} \right) $$

と表すことが出来ました。

まとめ

今回は、モード解析（Modal Analysis）を用いて求めたパラメータを用いて、実際に2質量システムがどのように振動するかを求める方法を紹介しました。

次回の記事では、今回求めた2質量システムの運動をグラフで表したいと思います。

モード解析を使って2質量システムの運動を求める：その３ モード解析（Modal Analysis）を用いることで、システムがどのように振動するかを求めることが出来ます。 ...