ラグランジュ方程式を用いてダンパーを含んだ剛体振り子の運動方程式を算出する

質量とばね、ダンパーからなるモデルについて、各エネルギーからラグランジュ方程式を用いてシステムの運動方程式を求める方法を紹介します。

この方法で求めた運動方程式は、ニュートンの運動の法則を用いた方法と同じになります。

ニュートンの運動の法則を用いたシステムの運動方程式の求め方は、こちらの記事を参考にしてください。

入力ありの質量-ばね-ダンパーモデルの運動を求める 今回は、質量-ばね-ダンパーモデルを用いて、入力として力が質量に与えられている場合のシステムの運動を考えます。 入...

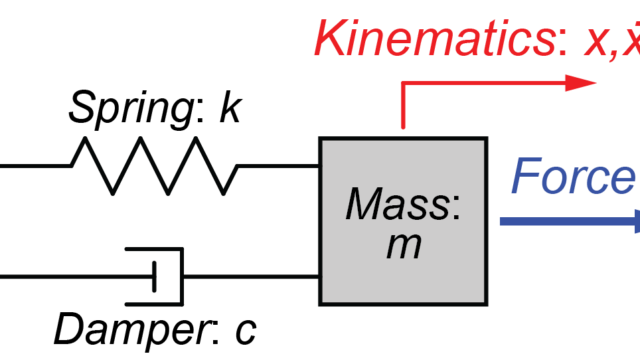
質量-ばね-ダンパーモデル

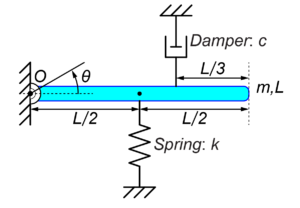
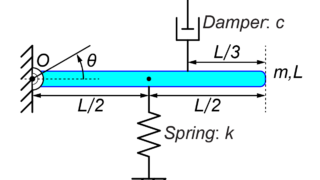
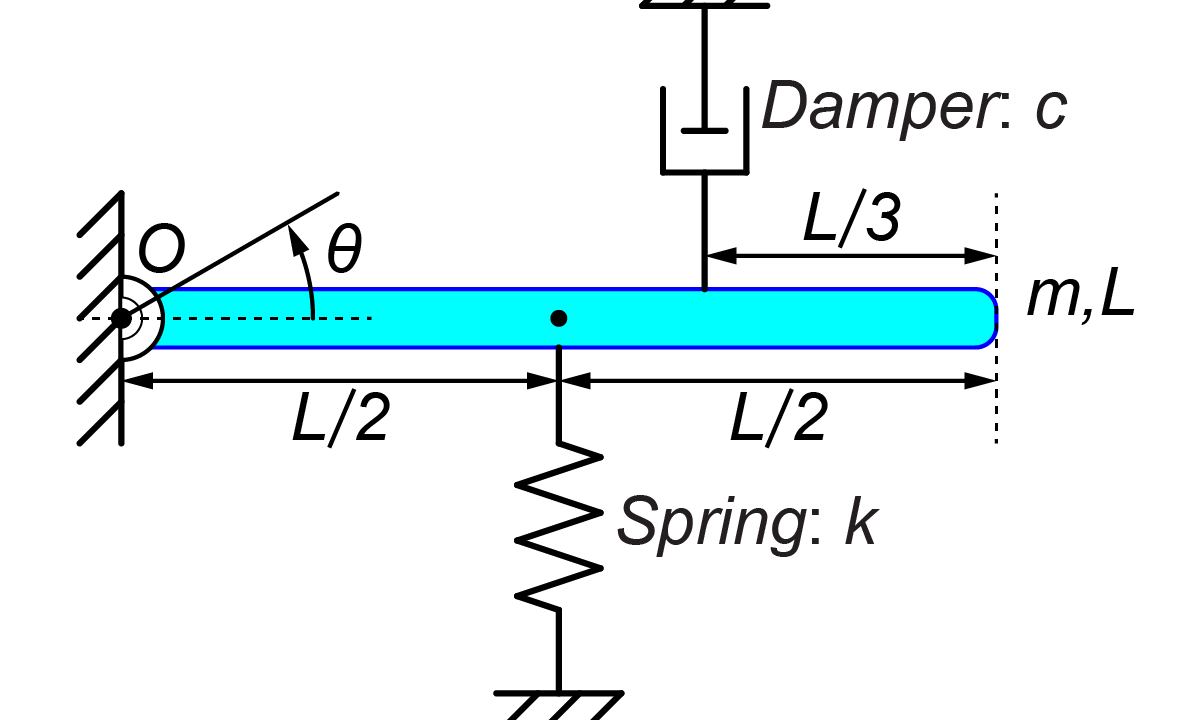
今回は、図のような棒状の長さ\(L\)の質量\(m\)が端点\(O\)で壁に接続され、その質量にばね\(k\)とダンパー\(c\)がついているモデルを扱います。

初期位置\(\theta_0\)で静かに棒を離したときに、どの様にシステムが運動するかを運動方程式を用いて考えます。

この運動方程式を用いることで、棒が時刻の経過によってどう振動していくかを求めることが出来ます。

各エネルギーと運動方程式の関係

エネルギー保存の法則とラグランジュ方程式を用いて、運動エネルギー（\(KE\)）と位置エネルギー（\(PE\)）が与えられた時のシステムの運動方程式は、

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = 0$$

という関係式で表すことが出来ます。

詳しくは、こちらの記事を参考にしてください。

剛体振り子の運動方程式を算出する 剛体振り子（Physical Pendulum）の運動方程式を求める方法を紹介します。 今回は、システムのエネルギ...

この式にダンパーによる影響を追加することで、質量-ばね-ダンパーシステムの運動方程式を求めていきます。

ダンパーによるエネルギーの損失と散逸関数

ダンパーにより損失するエネルギーを考慮し、この影響を踏まえて運動方程式を求めます。

ダンパーによる損失エネルギーは、速度\(\dot{x}\)の2乗に比例します。

ラグランジュ方程式にダンパーによるエネルギーの損失を考慮する場合は、散逸関数（Dissipation Function）を用います。

ダンパーの散逸関数（\(R_{NC}\)）は、

$$ R_{NC} = \frac{1}{2} c \dot{x}^2 $$

と表すことが出来ます。

今回のモデルの場合、この散逸関数はダンパーによってシステムがエネルギーを散逸する速度の半分になります。

ダンパーによるエネルギーの損失を考慮した運動方程式

先ほど求めたダンパーの散逸関数

$$ R_{NC} = \frac{1}{2} c \dot{x}^2 $$

を先のエネルギーと運動方程式の関係式

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = 0$$

に組み込みます。

ラグランジュ方程式にダンパーの散逸関数（\(R_{NC}\)）を考慮すると、

$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial \dot{x}} R_{NC} + \frac{\partial}{\partial x} PE = 0$$

となります。

この式を解くことでダンパーを含んだ運動方程式を求めることが出来ます。

まとめ

今回は、ばねとダンパーを含んだシステムの運動方程式を各エネルギーとラグランジュ方程式を用いて求める方法を紹介しました。

次回は、例として挙げた図のモデルについて、実際にシステムの運動を求めていきたいと思います。

実際にダンパーを含んだ剛体振り子の運動方程式を算出してみる ばねとダンパーが付いている棒からなる質量-ばね-ダンパーモデルについて、実際にシステムの運動方程式を求めていきます。 ...