ばねとダンパーが付いている棒からなる質量-ばね-ダンパーモデルについて、実際にシステムの運動方程式を求めていきます。
システムの詳しい説明は、こちらの記事を参考にしてください。
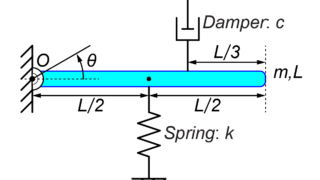
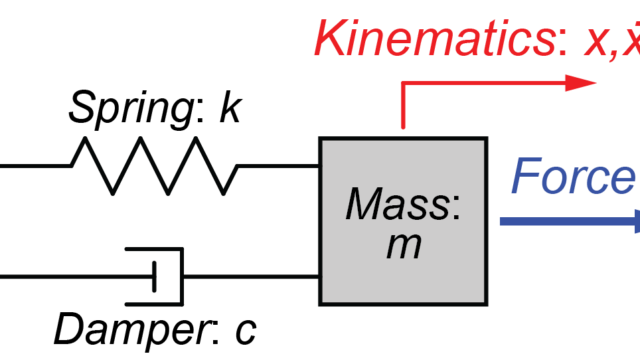
質量-ばね-ダンパーモデル

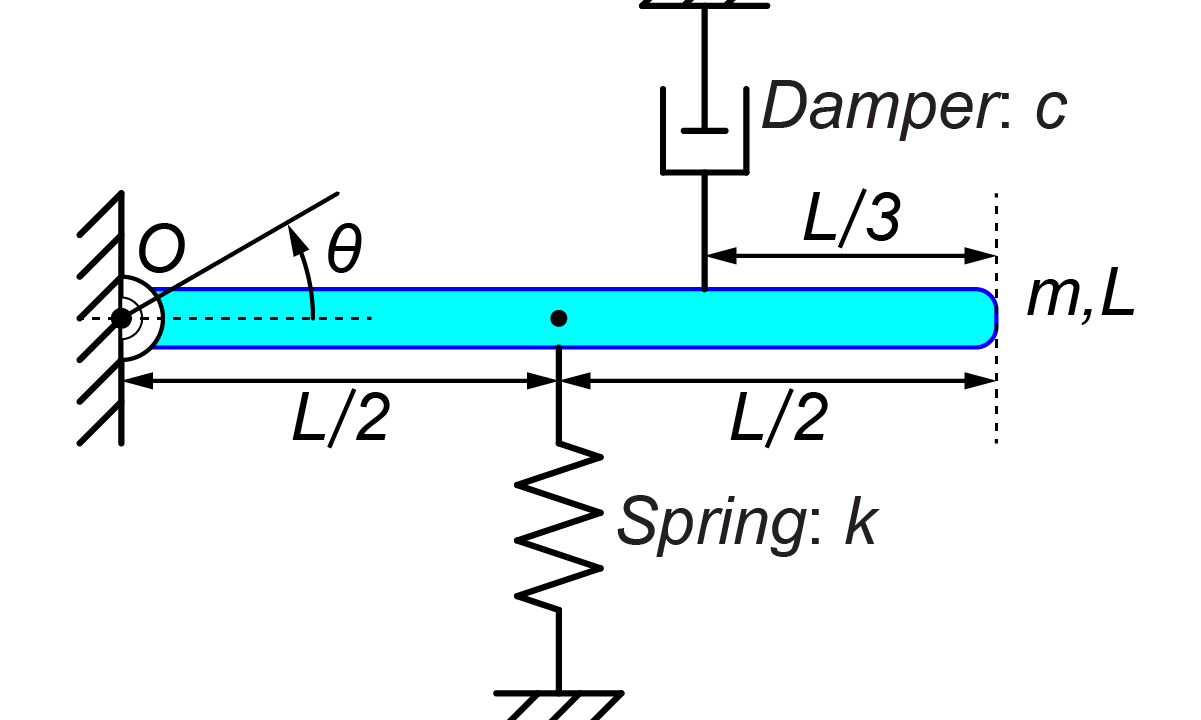
今回は、図のような質量mで長さLの棒が端点Oで壁に接続され、その質量にばねkとダンパーcがついているモデルを扱います。
初期位置θ0で静かに棒を離した場合、どの様にシステムが運動するかを運動方程式を用いて求めます。
各エネルギーとラグランジュ方程式を用いた運動方程式の算出方法
各エネルギーを
- 運動エネルギー(KE)
- 位置エネルギー(PE)
と、ダンパーによるエネルギー損失を示す
- 散逸関数(RNC)
とすると、ラグランジュ方程式を用いて、システムの運動方程式は、
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial \dot{x}} R_{NC} + \frac{\partial}{\partial x} PE = 0$$
と表すことが出来ます。
各エネルギーと散逸関数を求めて、この式に代入し解くことでシステムの運動方程式を求めることが出来ます。
各エネルギーと散逸関数の算出
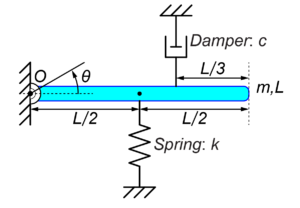
実際に図のシステムについて、各エネルギーと散逸関数を計算していきます。
運動エネルギー
回転運動する物体の運動エネルギーKEは、慣性モーメントIと角速度\(\dot{\theta}\)(またはω)の2乗に比例します。
物体が端点oを中心に回転した場合の慣性モーメントIoは、
$$ I_o = \frac{1}{3} m L^2 $$
と表すことが出来ます。
よって、このシステムの運動エネルギーは、
$$ \begin{eqnarray} KE &=& \frac{1}{2} I_o \dot{\theta}^2 \\ &=& \frac{1}{2} \left[\frac{1}{3} m L^2 \right] \dot{\theta}^2 \end{eqnarray} $$
となります。
位置エネルギー
ばねkによる位置エネルギーPEは、ばねの変位xの2乗に比例します。
今回のモデルについて、棒の角度がθの時のばねの変位xは、
$$ x = \frac{L}{2} \sin (\theta) $$
となります。ここで、角度θが小さいとすると、
$$ \sin (\theta) = \theta $$
と近似できるため、ばねの変位xは、
$$ x = \frac{L}{2} \theta $$
となります。
よって、このシステムの位置エネルギーは、
$$ \begin{eqnarray} PE &=& \frac{1}{2} k x^2 \\ &=& \frac{1}{2} k \left( \frac{L}{2} \theta \right)^2 \end{eqnarray} $$
となります。
散逸関数
ダンパーcによるエネルギーの損失を表す散逸関数RNCは、速度\(\dot{x}\)の2乗に比例します。
今回のモデルについて、棒の角度がθの時のダンパーの速度xは、角度θが小さいとすると、
$$ \dot{x} = \frac{2 L}{3} \dot{\theta} $$
と近似することが出来ます。
よって、このシステムの散逸関数は、
$$ \begin{eqnarray} R_{NC} &=& \frac{1}{2} c \dot{x}^2 \\ &=& \frac{1}{2} c \left( \frac{2 L}{3} \dot{\theta} \right)^2 \end{eqnarray} $$
となります。
このように、今回のシステムについて各エネルギーと散逸関数を算出することが出来ました。
運動方程式の算出
先に求めた2つのエネルギーと散逸関数をラグランジュ方程式に代入していきます。
$$ \begin{eqnarray} && \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial \dot{x}} R_{NC} + \frac{\partial}{\partial x} PE = 0 \\ && \Rightarrow \frac{d}{dt} \left( \frac{\partial}{\partial \dot{\theta}} \frac{1}{2} \left[\frac{1}{3} m L^2 \right] \dot{\theta}^2 \right) + \frac{\partial}{\partial \dot{\theta}} \frac{1}{2} c \left[ \frac{4}{9} L^2 \right] \dot{\theta}^2 + \frac{\partial}{\partial \theta} \frac{1}{2} k \left[ \frac{1}{4} L^2 \right] \theta ^2 = 0 \\ && \Rightarrow \frac{1}{3} m L^2 \ddot{\theta} + \frac{4}{9} c L^2 \dot{\theta} + \frac{1}{4} k L^2 \theta = 0 \end{eqnarray}$$
このように、各エネルギーと散逸関数からラグランジュ方程式を用いてシステムの運動方程式を求めることが出来ました。
まとめ
今回は、実際に質量-ばね-ダンパーモデルを例にとって、システムの運動方程式を求める方法を紹介しました。
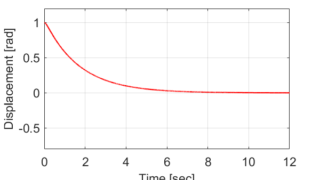
次回は、今回求めたシステムの運動方程式から初期条件を使って実際のモデルの運動、振動の様子を計算していきたいと思います。
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
