伝達関数で質量‐ばね‐ダンパーシステムを表す

今回は、伝達関数を使って質量‐ばね‐ダンパーシステムを表していきたいと思います。

線形微分方程式を用いて同じシステムを表した結果はこの記事を参考にして下さい。

質量‐ばね‐ダンパーシステムを線形微分方程式で表す 今回は、過去に紹介した線形微分方程式（Differential Equation）を用いて、質量‐ばね‐ダンパーシステム（Mas...

伝達関数を使ったシステムモデル

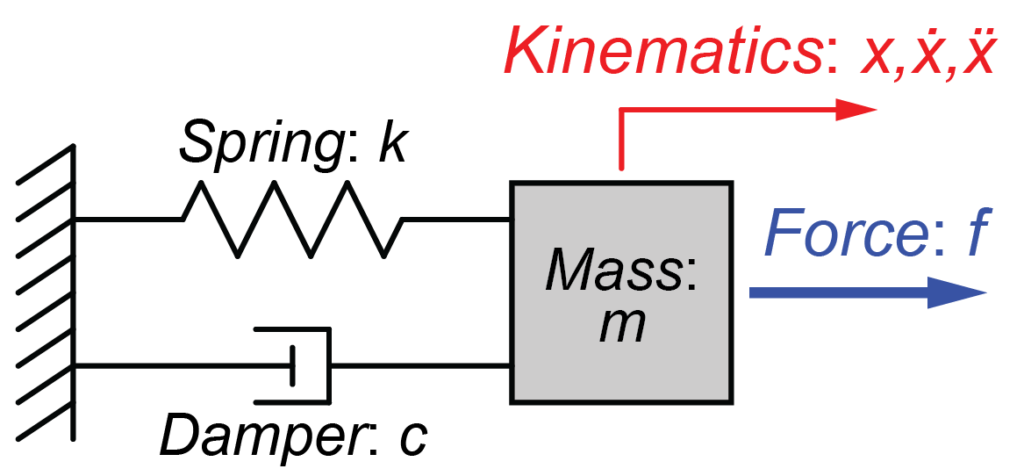
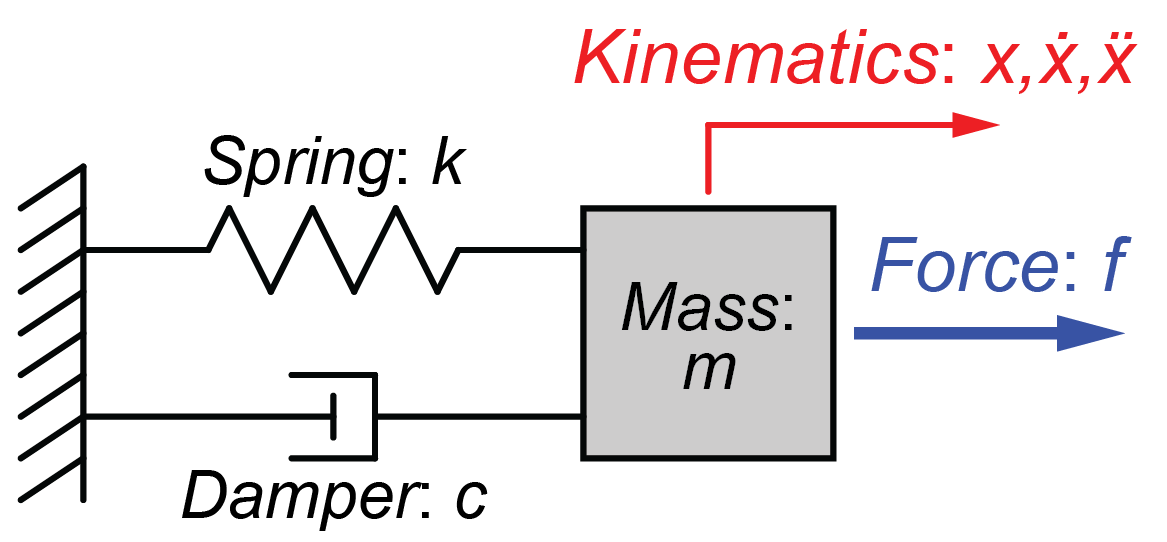
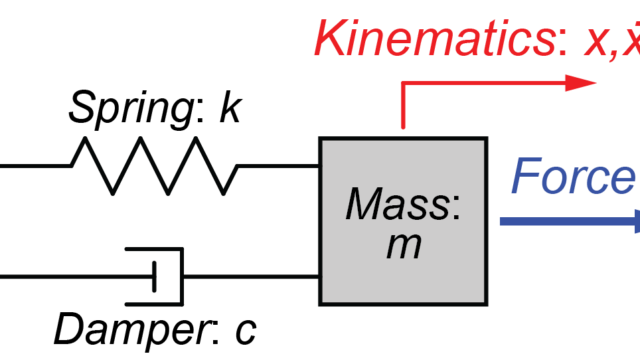
質量‐ばね‐ダンパーシステムを線形微分方程式で表すと、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t) $$

となります。

この時間領域\(t\)での線形微分方程式をラプラス変換を用いて複素数領域\(s\)に変換します。

両辺をラプラス変換すると、

$$ m s^2 X(s) + c s X(s) + k X(s) = F(s) $$

となります。

ラプラス変換に関する詳しい解説は、こちらの記事を参考にして下さい。

ラプラス変換を用いてシステムを伝達関数で表す 前回は、線形時不変システム（LTIシステム）を説明しました。 ただ、動的システムに対してLTIシステムのモデルを用いると計...

伝達関数\(G(s)\)は、入力\(F(s)\)と出力\(X(s)\)の比なので、

$$ G(s) = \frac{X(s)}{F(s)} = \frac{1}{m s^2 + c s + k} $$

と表すことが出来ます。

システムをブロック線図を使って表す

先ほど求めたシステムをブロック線図で表していきます。

入力\(F(s)\)に対する出力が\(X(s)\)となる伝達関数\(G(s)\)は、

と表すことが出来ます。

このようなシステム\(G(s)\)を２次系（Second-order System）と言います。

このシステムは各要素に分解してブロック線図にすると、

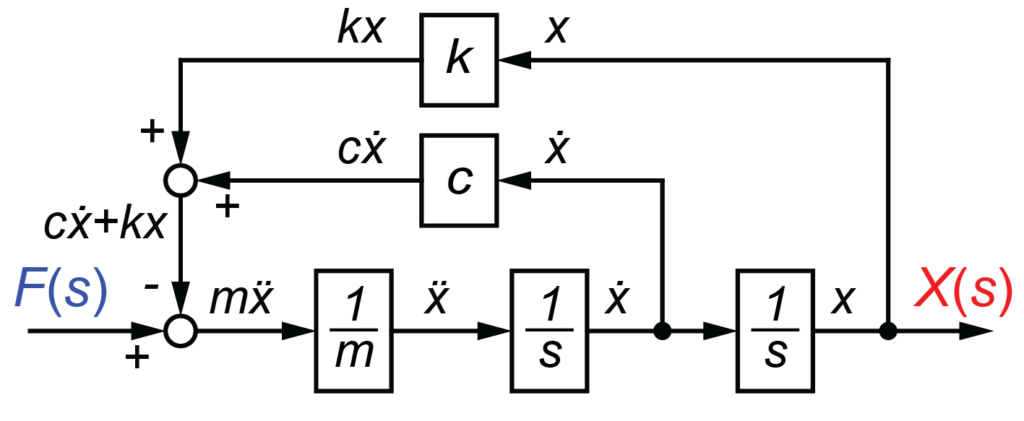
と表すこともできます。

まとめ

今回は動的システムを伝達関数で表してみました。

今回のような伝達関数を用いることで、システムの出力に新しく何かを加えた場合でも伝達関数同士の積で表すことが可能となります。

そのため複雑になりがちな動的システム同士を組み合わせる場合もシンプルに扱うことが出来ます。