状態空間モデルを用いて動的システムを表す

今回は動的システムを状態空間モデル（State Space Model）で表す方法を紹介します。

Contents

状態空間モデルとは
質量-ばね-ダンパーシステムの状態空間モデル
- 状態方程式
- 出力方程式
まとめ

状態空間モデルとは

入力が$u$で出力が$y$とした時の状態空間モデルは、

$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } + \boldsymbol{ B } u \\ y = \boldsymbol{ C } \boldsymbol{ x } + D u \end{array} \right. \end{eqnarray} $$

となります。

$x$は状態ベクトルというもので、システムの状態を示しています。

$$ \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} $$

状態空間モデルの内、1つ目の$\dot{x}$についての式が状態方程式と呼ばれます。

システムの状態$x$が入力$u$によってどう変化するかを表しています。

2つ目の$y$についての式は、出力方程式と呼ばれます。

システムの状態$x$および入力$u$と観測する出力$y$との関係を示しています。

質量-ばね-ダンパーシステムの状態空間モデル

質量-ばね-ダンパーシステムを例に実際に状態空間モデルを求めていきます。

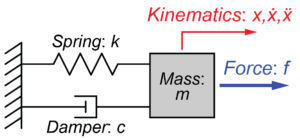
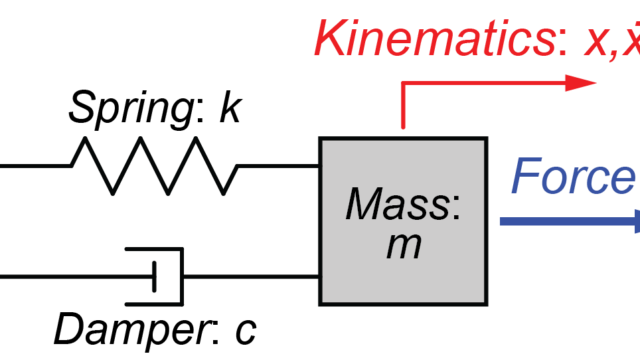
このシステムの線形微分方程式は、

$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t) $$

と表されます。

詳しくは、この記事を参照してください。

質量‐ばね‐ダンパーシステムを線形微分方程式で表す今回は、過去に紹介した線形微分方程式（Differential Equation）を用いて、質量‐ばね‐ダンパーシステム（Mas...

状態方程式

システムの線形微分方程式を$\ddot{x}$についての式にすると、

$$ \ddot{x}(t) = – \frac{c}{m} \dot{x}(t) – \frac{k}{m} x(t) + \frac{1}{m} f(t) $$

となります。

状態ベクトルを

$$ \boldsymbol{ x } = \begin{bmatrix} \dot{x} \\ x \end{bmatrix} $$

とすると、状態方程式は、

$$ \boldsymbol{ \dot{x} } = \begin{bmatrix} \ddot{x} \\ \dot{x} \end{bmatrix} = \begin{bmatrix} -\frac{c}{m} & -\frac{k}{m} \\ 1 & 0 \end{bmatrix} \boldsymbol{ x } + \begin{bmatrix} \frac{1}{m} \\ 0 \end{bmatrix} f = \begin{bmatrix} -\frac{c}{m} & -\frac{k}{m} \\ 1 & 0 \end{bmatrix} \begin{bmatrix} \dot{x} \\ x \end{bmatrix} + \begin{bmatrix} \frac{1}{m} \\ 0 \end{bmatrix} f $$

と表すことが出来ます。

実際にこの状態方程式を計算（展開）してみると、

$$ \ddot{x}(t) = – \frac{c}{m} \dot{x}(t) – \frac{k}{m} x(t) + \frac{1}{m} f(t) $$

$$ \dot{x}(t) = \dot{x}(t) $$

となり、求めた状態方程式が正しいことが分かります。

出力方程式

観測したい出力$y$を

$$ y = x $$

とすると、出力方程式は、

$$ y = \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} \dot{x} \\ x \end{bmatrix} + \begin{bmatrix} 0 \end{bmatrix} f $$

となります。

実際にこの出力方程式を計算してみると、

$$ y = x $$

となり、求めた出力方程式が正しいことが分かります。

よって、質量-ばね-ダンパーシステムの状態空間モデルにおける各行列およびベクトルは、

$$ \boldsymbol{ A } = \begin{bmatrix} -\frac{c}{m} & -\frac{k}{m} \\ 1 & 0 \end{bmatrix} , \boldsymbol{ B } = \begin{bmatrix} \frac{1}{m} \\ 0 \end{bmatrix} , \boldsymbol{ C } = \begin{bmatrix} 0 & 1 \end{bmatrix} , D = \begin{bmatrix} 0 \end{bmatrix} $$

となります。