今回はこれまで求めてきたMIMOシステムの運動方程式を基に、2質量系モデルの伝達関数を実際に求めていきます。
2質量系モデルの伝達関数ついての詳細は、この記事を参考にしてください。

MIMOシステムの線形微分方程式とラプラス変換
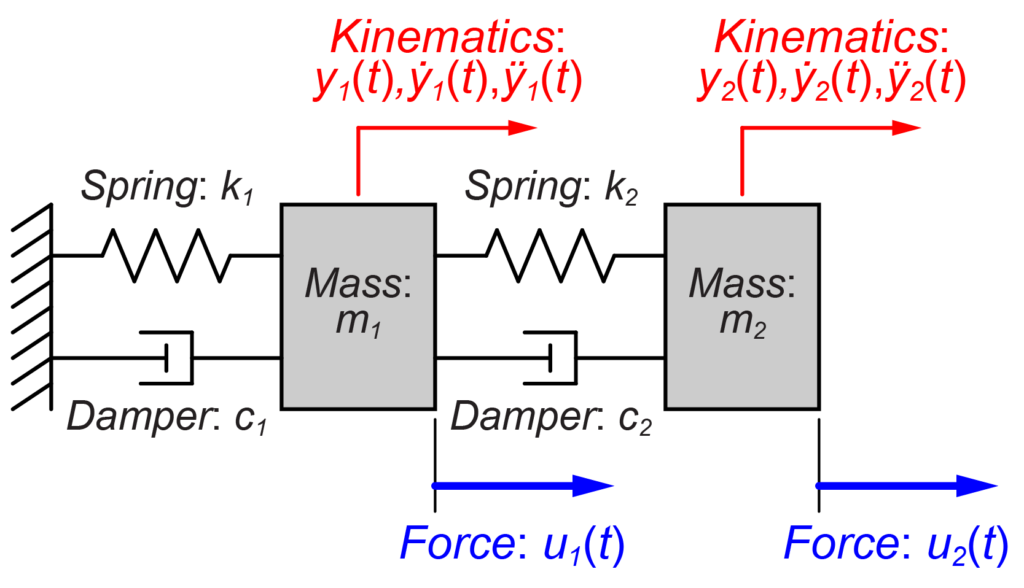
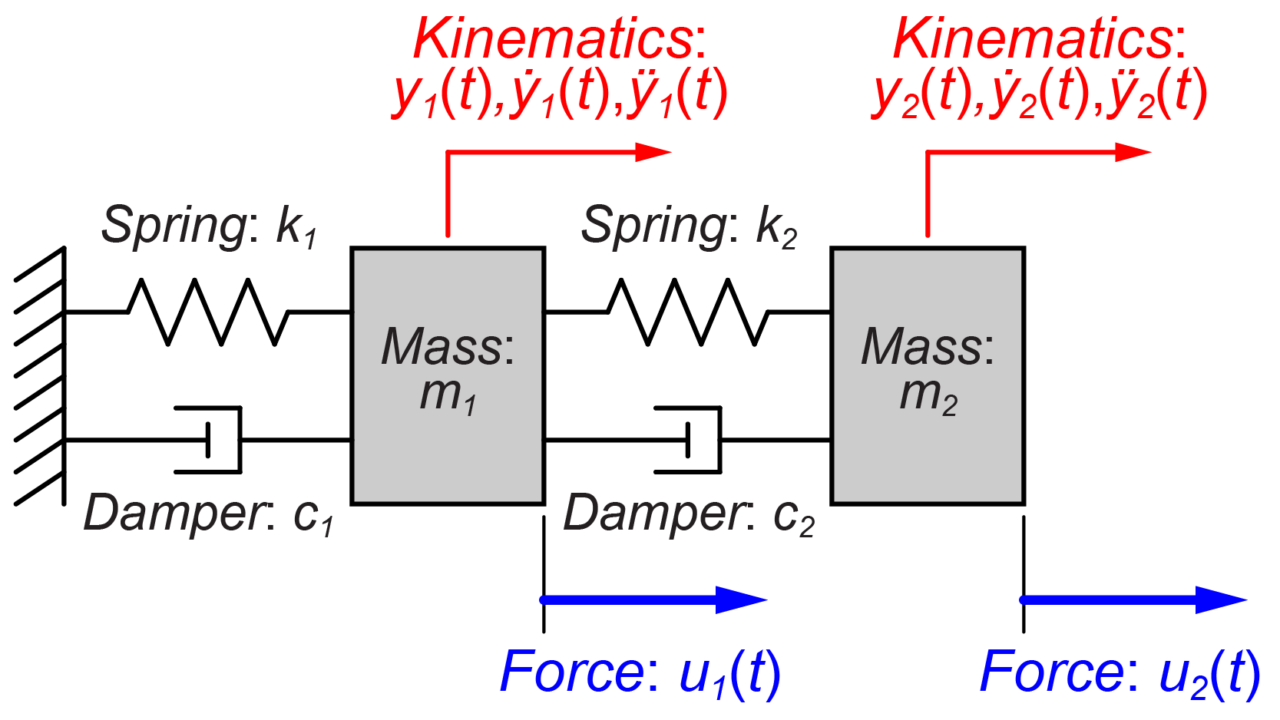
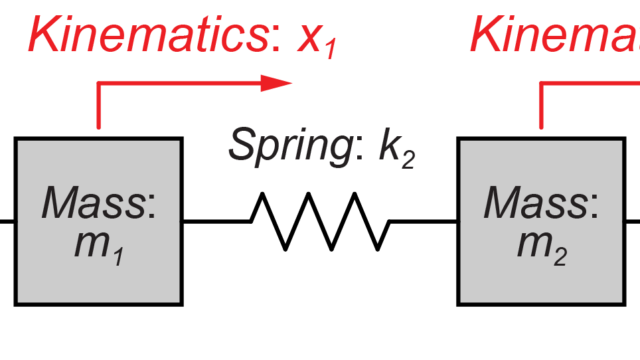
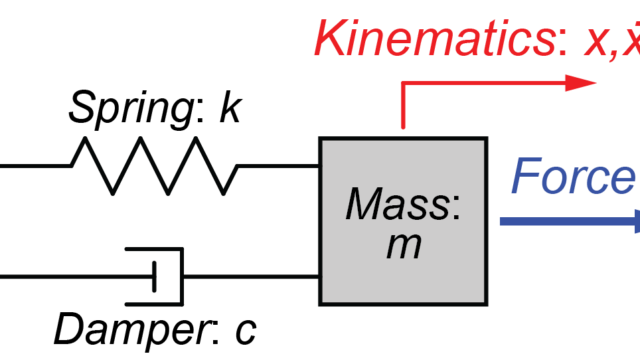
この2質量系MIMOシステムの線形微分方程式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{y_1}(t) + \left(c_1+c_2\right) \dot{y_1}(t) + \left(k_1+k_2\right) y_1(t) – c_2 \dot{y_2}(t) – k_2 y_2(t) = u_1(t) \\ m_2 \ddot{y_2}(t) + c_2 \dot{y_2}(t) + k_2 y_2(t) – c_2 \dot{y_1}(t) – k_2 y_1(t) = u_2(t) \end{array} \right. \end{eqnarray} $$
となります。
2質量系モデルの線形微分方程式(運動方程式)については、この記事を参考にしてください。
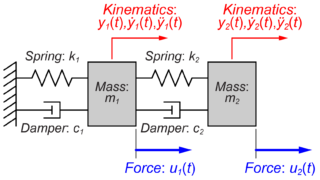
この2式についてそれぞれラプラス変換して時間領域tから複素数領域sで表します。
$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right) \right) Y_1(s) – \left( c_2 s + k_2 \right) Y_2(s) = U_1(s) \\ \left( m_2 s^2 + c_2 s + k_2 \right) Y_2(s) – \left( c_2 s + k_2 \right) Y_1(s) = U_2(s) \end{array} \right. \end{eqnarray} $$
このラプラス変換した2式を用いて伝達関数(入力と出力の関係)を示していきます。
MIMOシステムの伝達関数
MIMOシステムの伝達関数は一般的に、
$$ \begin{bmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_m \end{bmatrix} = \begin{bmatrix} G_{11} & G_{12} & \cdots & G_{1l} \\ G_{21} & G_{22} & \cdots & G_{2l} \\ \vdots & \vdots & \ddots & \vdots \\ G_{m1} & G_{m2} & \cdots & G_{ml} \end{bmatrix} \begin{bmatrix} U_1 \\ U_2 \\ \vdots \\ U_l \end{bmatrix} $$
と定義されます。
MIMOシステム全体の伝達関数を求めるために個々の入力(U1(s)とU2(s))と出力(Y1(s)とY2(s))の伝達関数を求めていきます。
入力U1(s)に対する伝達関数
入力U1(s)に対する出力Y1(s)とY2(s)の関係を求めるために、入力U2(s)を除いて(0にして)入力U1(s)のみのシステムとして伝達関数を算出していきます。
入力がU1(s)だけの場合のラプラス変換の式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right) \right) Y_1(s) – \left( c_2 s + k_2 \right) Y_2(s) = U_1(s) \\ \left( m_2 s^2 + c_2 s + k_2 \right) Y_2(s) – \left( c_2 s + k_2 \right) Y_1(s) = 0 \end{array} \right. \end{eqnarray} $$
となります。
この2式を連立方程式として、各出力(Y1(s)とY2(s))について解いていきます。
2つ目の式からY2(s)をY1(s)を用いて表した式が得られます。
$$ \begin{eqnarray} \left( m_2 s^2 + c_2 s + k_2 \right) Y_2(s) – \left( c_2 s + k_2 \right) Y_1(s) = 0 \\ \Rightarrow Y_2(s) = \frac{c_2 s + k_2}{m_2 s^2 + c_2 s + k_2} Y_1(s) \end{eqnarray} $$
この式を1つ目の式に代入して整理すると、
$$ \begin{eqnarray} \left( m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right) \right) Y_1(s) – \left( c_2 s + k_2 \right) \frac{c_2 s + k_2}{m_2 s^2 + c_2 s + k_2} Y_1(s) = U_1(s) \\ \Rightarrow \left( m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right) – \frac{\left( c_2 s + k_2 \right) ^2}{m_2 s^2 + c_2 s + k_2} \right) Y_1(s) = U_1(s) \end{eqnarray} $$
となります。
よって、入力U1(s)に対する出力Y1(s)の伝達関数G11(s)は、
$$ \begin{eqnarray} G_{11}(s) = \frac{Y_1(s)}{U_1(s)} = \frac{m_2 s^2 + c_2 s + k_2}{ \left( m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right) \right) \left( m_2 s^2 + c_2 s + k_2 \right) – \left( c_2 s + k_2 \right) ^2} \\ \Rightarrow G_{11}(s) =\frac{m_2 s^2 + c_2 s + k_2}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } \end{eqnarray} $$
と表すことが出来ます。
つぎに出力Y2(s)について解いていきます。
2つ目の式から求めたY2(s)についての式と先ほど求めた伝達関数から、
$$ Y_2(s) = \frac{c_2 s + k_2}{m_2 s^2 + c_2 s + k_2} G_{11}(s) U_1(s) $$
と表されます。
よって、入力U1(s)に対する出力Y2(s)の伝達関数G21(s)は、
$$ G_{21}(s) = \frac{Y_2(s)}{U_1(s)} =\frac{c_2 s + k_2}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } $$
となります。
入力U2(s)に対する伝達関数
入力U1(s)の場合と同様に、入力U2(s)に対する出力Y1(s)とY2(s)の伝達関数を求めていきます。
入力がU2(s)だけの場合のラプラス変換の式は、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right) \right) Y_1(s) – \left( c_2 s + k_2 \right) Y_2(s) = 0 \\ \left( m_2 s^2 + c_2 s + k_2 \right) Y_2(s) – \left( c_2 s + k_2 \right) Y_1(s) = U_2(s) \end{array} \right. \end{eqnarray} $$
となります。
1つ目の式から、Y2(s)についてY1(s)を用いて表した式が得られます。
$$ Y_2(s) = \frac{m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right)}{c_2 s + k_2} Y_1(s) $$
この式を2つ目の式に代入して整理すると、
$$ \begin{eqnarray} \left( m_2 s^2 + c_2 s + k_2 \right) \frac{m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right)}{c_2 s + k_2} Y_1(s) – \left( c_2 s + k_2 \right) Y_1(s) = U_2(s) \\ \Rightarrow \left( \left( m_2 s^2 + c_2 s + k_2 \right) \frac{m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right)}{c_2 s + k_2} – \left( c_2 s + k_2 \right) \right) Y_1(s) = U_2(s) \end{eqnarray} $$
となります。
よって、入力U2(s)に対する出力Y1(s)の伝達関数G12(s)は、
$$ G_{12}(s) = \frac{Y_1(s)}{U_2(s)} =\frac{c_2 s + k_2}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } $$
と表すことが出来ます。
つぎに出力Y2(s)について解いていきます。
1つ目の式から求めたY2(s)についての式と先ほど求めた伝達関数G12(s)から、
$$ Y_2(s) = \frac{m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right)}{c_2 s + k_2} G_{12}(s) U_2(s) $$
よって、入力U2(s)に対する出力Y2(s)の伝達関数G22(s)は、
$$ G_{22}(s) = \frac{Y_2(s)}{U_2(s)} =\frac{m_1 s^2 + \left(c_1+c_2\right) s + \left(k_1+k_2\right)}{ \left( m_1 s^2 + c_1 s + k_1 \right) \left( m_2 s^2 + c_2 s + k_2 \right) + m_2 s^2 \left( c_2 s + k_2 \right) } $$
となります。
これら個別で求めた各入力に対する各出力の伝達関数を行列でまとめると、MIMOシステム全体の伝達関数を表現することが出来ます。
まとめ
今回は2入力2出力のMIMOシステムについて、伝達関数を求める方法を紹介しました。
MIMOは複雑な印象がありますが、一つ一つ丁寧に解いていけばSISOシステムと同様に問題を解くことが可能です。
合わせて読みたい
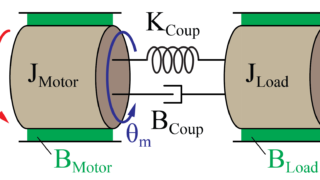
回転運動モデルの場合はこちら

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
