状態方程式で2質量システム（MIMOシステム）を表す

前回算出した運動方程式を用いて、2質量系モデルの状態方程式を求めていきます。

運動方程式を算出した前回の記事はこちら。

2質量システム（MIMOシステム）の運動方程式を求める MIMO系の状態方程式（状態空間モデル）や伝達関数について、実際に例題を解きながら求めていきたいと思います。 MI...

Contents

MIMOシステムの運動方程式
MIMOシステムの状態方程式
まとめ

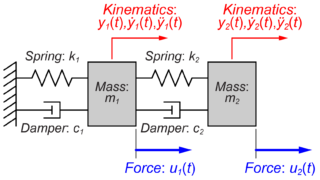
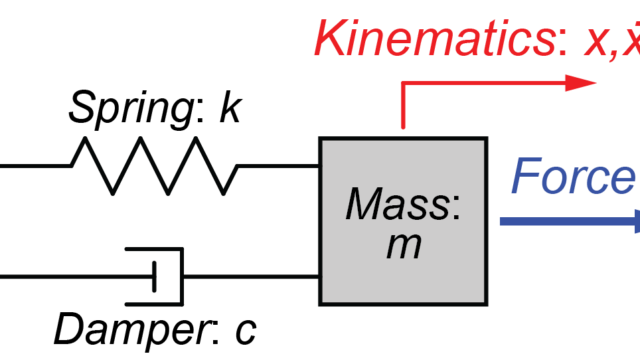
MIMOシステムの運動方程式

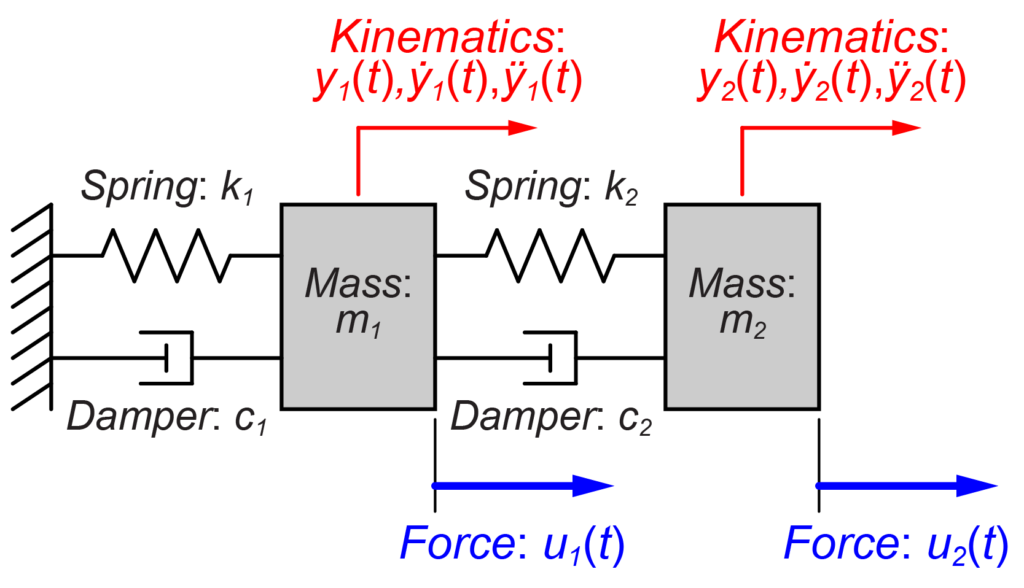
このモデルの運動方程式は、

$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{y_1}(t) = u_1(t) – k_1 y_1(t) – c_1 \dot{y_1}(t) + k_2 \left( y_2(t) – y_1(t) \right) + c_2 \left( \dot{y_2}(t) – \dot{y_1}(t) \right) \\ m_2 \ddot{y_2}(t) = u_2(t) – k_2 \left( y_2(t) – y_1(t) \right) – c_2 \left( \dot{y_2}(t) – \dot{y_1}(t) \right) \end{array} \right. \end{eqnarray} $$

となります。

この運動方程式を線形微分方程式の基本形に変換すると、

$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{y_1}(t) + \left(c_1+c_2\right) \dot{y_1}(t) + \left(k_1+k_2\right) y_1(t) – c_2 \dot{y_2}(t) – k_2 y_2(t) = u_1(t) \\ m_2 \ddot{y_2}(t) + c_2 \dot{y_2}(t) + k_2 y_2(t) – c_2 \dot{y_1}(t) – k_2 y_1(t) = u_2(t) \end{array} \right. \end{eqnarray} $$

となります。

線形微分方程式については、こちらの記事を参考にしてください。

質量‐ばね‐ダンパーシステムを線形微分方程式で表す今回は、過去に紹介した線形微分方程式（Differential Equation）を用いて、質量‐ばね‐ダンパーシステム（Mas...

この2入力2出力のMIMO系システムをSISO系システムと同じように一つの式にまとめると、

$$ \boldsymbol{M} \boldsymbol{\ddot{y}} + \boldsymbol{C} \boldsymbol{\dot{y}} +\boldsymbol{K} \boldsymbol{y} = \boldsymbol{u} $$

$$ \Rightarrow \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix} \begin{bmatrix} \ddot{y_1} \\ \ddot{y_2} \end{bmatrix} + \begin{bmatrix} c_1+c_2 & -c_2 \\ -c_2 & c_2 \end{bmatrix} \begin{bmatrix} \dot{y_1} \\ \dot{y_2} \end{bmatrix} + \begin{bmatrix} k_1+k_2 & -k_2 \\ -k_2 & k_2 \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} $$

と行列で表すことが出来ます。

MIMOシステムの状態方程式

システムの運動方程式を変換して、加速度についての式に変形します。

$$ \ddot{y_1}(t) = – \frac{k_1+k_2}{m_1} y_1(t) – \frac{c_1+c_2}{m_1} \dot{y_1}(t) + \frac{k_2}{m_1} y_2(t) + \frac{c_2}{m_1} \dot{y_2}(t) + \frac{1}{m_1} u_1(t) $$

$$ \ddot{y_2}(t) = \frac{k_2}{m_2} y_1(t) + \frac{c_2}{m_2} \dot{y_1}(t) – \frac{k_2}{m_2} y_2(t) – \frac{c_2}{m_2} \dot{y_2}(t) + \frac{1}{m_2} u_2(t) $$

システムの状態を示す状態ベクトル$\boldsymbol{x}$と入力ベクトル$\boldsymbol{u}$、出力ベクトル$\boldsymbol{y}$を

$$ \boldsymbol{x} = \begin{bmatrix} y_1 \\ \dot{y_1} \\ y_2 \\ \dot{y_2} \end{bmatrix} $$

$$ \boldsymbol{u} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} $$

$$ \boldsymbol{y} = \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} $$

この時の状態方程式は、

$$ \boldsymbol{\dot{x}} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{k_1+k_2}{m_1} & – \frac{c_1+c_2}{m_1} & \frac{k_2}{m_1} & \frac{c_2}{m_1} \\ 0 & 0 & 0 & 1 \\ \frac{k_2}{m_2} & \frac{c_2}{m_2} & – \frac{k_2}{m_2} & – \frac{c_2}{m_2} \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 0 & 0 \\ \frac{1}{m_1} & 0 \\ 0 & 0 \\ 0 & \frac{1}{m_2} \end{bmatrix} \boldsymbol{u} $$

$$ \boldsymbol{y} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \boldsymbol{u} $$

と表すことが出来ます。

例題の2質量系システムを状態方程式（状態空間モデル）で表した時の各パラメータ行列は、

$$ \boldsymbol{A} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ – \frac{k_1+k_2}{m_1} & – \frac{c_1+c_2}{m_1} & \frac{k_2}{m_1} & \frac{c_2}{m_1} \\ 0 & 0 & 0 & 1 \\ \frac{k_2}{m_2} & \frac{c_2}{m_2} & – \frac{k_2}{m_2} & – \frac{c_2}{m_2} \end{bmatrix} $$

$$ \boldsymbol{B} = \begin{bmatrix} 0 & 0 \\ \frac{1}{m_1} & 0 \\ 0 & 0 \\ 0 & \frac{1}{m_2} \end{bmatrix} $$

$$ \boldsymbol{C} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} $$

$$ \boldsymbol{D} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} $$

になります。