2質量システム（MIMOシステム）の運動方程式を求める

MIMO系の状態方程式（状態空間モデル）や伝達関数について、実際に例題を解きながら求めていきたいと思います。

MIMO系の状態方程式と伝達関数についての詳細は、この記事を参考にして下さい。

多入力・多出力のシステム　MIMO系の伝達関数と状態方程式（状態空間モデル） 入力数と出力数が各々1つのシステムをSISI（Single Input Single Output）系と言います。 ...

２質量システム

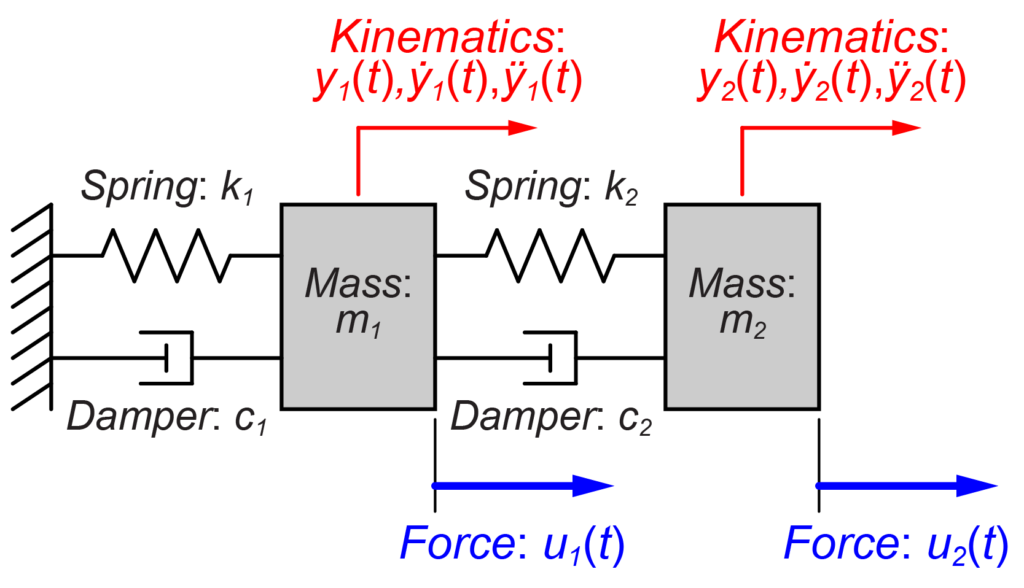
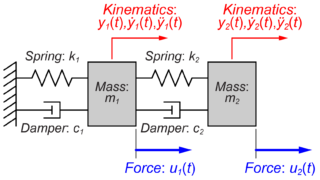
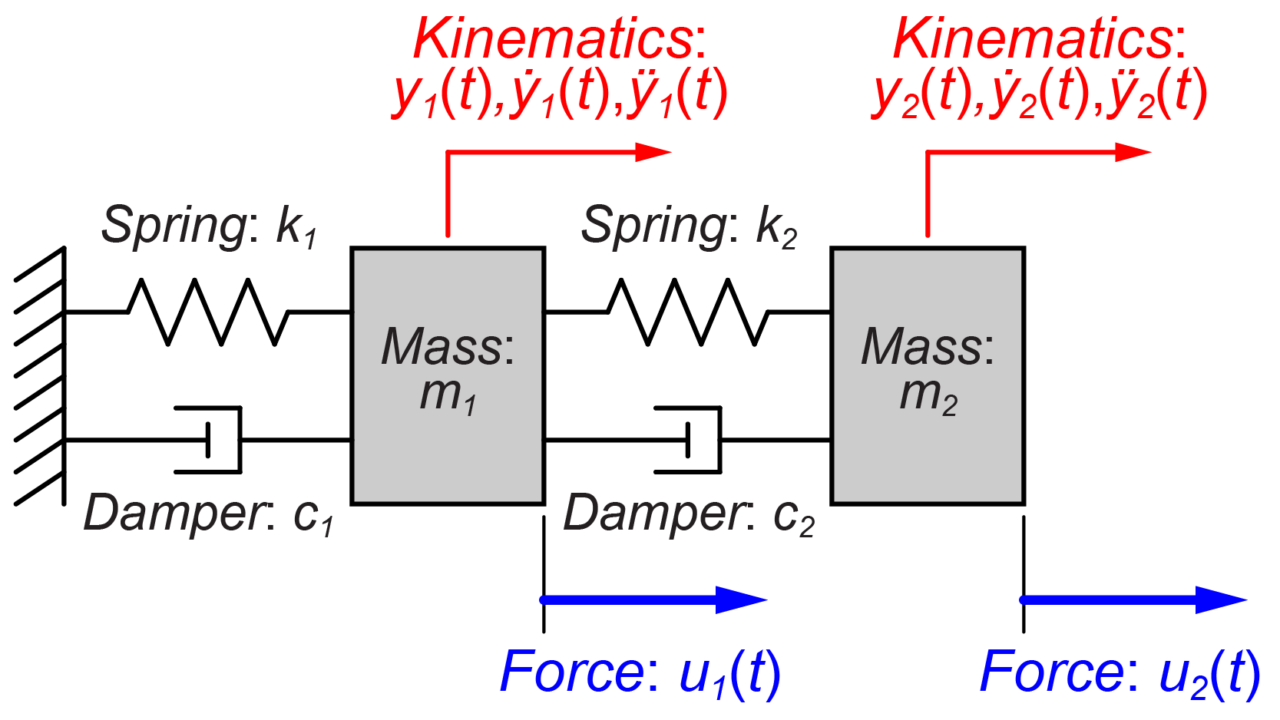
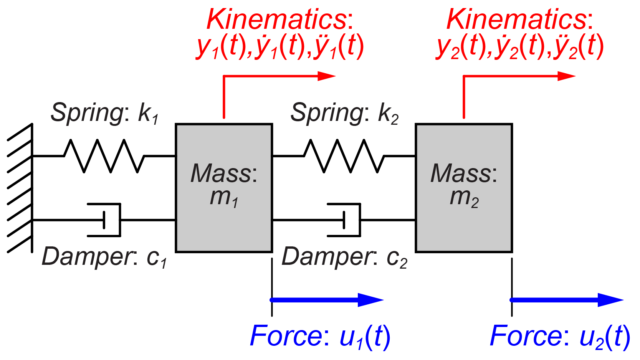
今回は、このような多入力、多出力システムについて考えていきます。

まず、質量\(m_1\)がばね\(k_1\)とダンパー\(c_1\)で壁に取り付けられています。

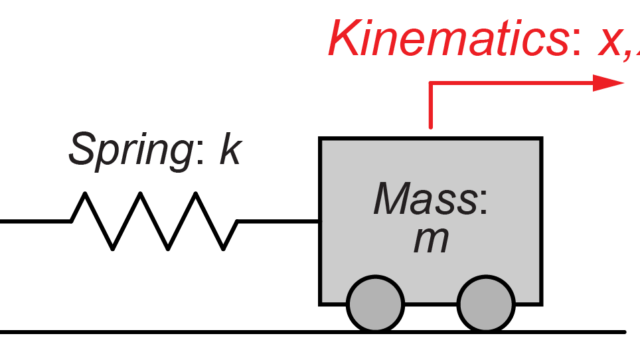
これだけなら、SISO系のモデル（入力：\(u_1\)、出力：\(y_1\)）として簡単に解くことが出来ます。

SISO系システムの解き方については、この記事を参考にしてください。

質量‐ばね‐ダンパーシステムを線形微分方程式で表す 今回は、過去に紹介した線形微分方程式（Differential Equation）を用いて、質量‐ばね‐ダンパーシステム（Mas...

加えて質量\(m_2\)がばね\(k_2\)とダンパー\(c_2\)で質量\(m_1\)に取り付けられています。

質量（\(m_1\)と\(m_2\)）にそれぞれ入力として力（\(u_1\)と\(u_2\)）が加わった時の各質量の変位（\(y_1\)と\(y_2\)）を出力を求めたいと思います。

このシステムの入出力は

• 入力：\(u_1\)、\(u_2\)
• 出力：\(y_1\)、\(y_2\)

と２つ以上なので、この２質量系のシステムはMIMO系システムとなります。

MIMOシステムの運動方程式

例題の２質量システムについて運動方程式を求めていきます。

運動方程式については、この記事を参考にしてください

質量‐ばね‐ダンパーシステムを線形微分方程式で表す 今回は、過去に紹介した線形微分方程式（Differential Equation）を用いて、質量‐ばね‐ダンパーシステム（Mas...

MIMOシステムの運動方程式を求めるために、各質量（\(m_1\)と\(m_2\)）についてそれぞれの運動方程式を求めます。

質量\(m_1\)についての運動方程式

質量\(m_1\)の加速度は\(\ddot{y_1}\)で表すことが出来ます。

（\(\ddot{y_1}\)は\(y_1\)の二階微分です。）

質量\(m_1\)にかかる力\(f\)は入力\(u_1\)です。

そして左側のばね\(k_1\)とダンパー\(c_1\)から受ける力は、

$$ f_{k_1} = k_1 y_1 $$

$$ f_{c_1} = c_1 \dot{y_1} $$

となります。

向きは左向き（変位\(y_1\)と逆向き）になります。

次に右側のばね\(k_2\)とダンパー\(c_2\)から受ける力を求めていきます。

ばね\(k_2\)による力を計算するために、ばねにかかる変位を考えていきます。

図からばね\(k_2\)の変位は\(y_2 – y_1\)で求められます。

この時のばね\(k_2\)による力は、

$$ f_{k_2} = k_2 \left( y_2 – y_1 \right) $$

となります。

この力\(f_{k_2}\)の向きは右向き（変位\(y_1\)と同じ向き）になります。

ばね\(k_2\)が伸びる（\(y_2 – y_1\)が大きくなる）ほど、ばね\(k_2\)は縮もうとします。

その結果、質量\(m_1\)を右に引くからです。

次に、ダンパ―\(c_2\)による力を計算するために、ダンパー\(c_2\)にかかる速度を考えていきます。

図からダンパー\(c_2\)の速度は\(\dot{y_2} – \dot{y_1}\)で求められます。

この時のダンパー\(c_2\)による力は、

$$ f_{c_2} = c_2 \left( \dot{y_2} – \dot{y_1} \right) $$

となります。

この力\(f_{c_2}\)の向きは右向き（変位\(y_1\)と同じ向き）になります。

ばね\(k_2\)の時と同様に、ダンパー\(c_2\)が伸びる（\(\dot{y_2} – \dot{y_1}\)が大きくなる）ほど、ダンパー\(c_2\)はそれを防ごうとして、質量\(m_1\)から右に力\(f_{c_2}\)を与えます。

よって、質量\(m_1\)についての運動方程式は、

$$ m_1 \ddot{y_1} = u_1 – k_1 y_1 – c_1 \dot{y_1} + k_2 \left( y_2 – y_1 \right) + c_2 \left( \dot{y_2} – \dot{y_1} \right) $$

となります。

質量\(m_2\)についての運動方程式

質量\(m_1\)の流れと同様に、質量\(m_2\)まわりの運動方程式を求めていきます。

質量\(m_2\)の加速度は\(\ddot{y_2}\)で表すことが出来ます。

（\(\ddot{y_2}\)は\(y_2\)の二階微分です。）

質量\(m_2\)にかかる力\(f\)は入力\(u_2\)です。

そしてばね\(k_2\)とダンパー\(c_2\)から受ける力は、

$$ f_{k_2} = k_2 \left( y_2 – y_1 \right) $$

$$ f_{c_2} = c_2 \left( \dot{y_2} – \dot{y_1} \right) $$

となります。

向きは左向き（変位\(y_2\)と逆向き）になります。

よって、質量\(m_2\)についての運動方程式は、

$$ m_2 \ddot{y_2} = u_2 – k_2 \left( y_2 – y_1 \right) – c_2 \left( \dot{y_2} – \dot{y_1} \right) $$

となります。

まとめ

今回は、2質量系モデルの運動方程式の算出までを行いました。

次回は、算出した運動方程式を使ってMIMOシステムの状態方程式と伝達関数を求めていきます。

（つづく）

状態方程式で2質量システム（MIMOシステム）を表す2質量システムを例に、実際にMIMO系システムの運動方程式から状態方程式を求める方法を紹介します。...

合わせて読みたい

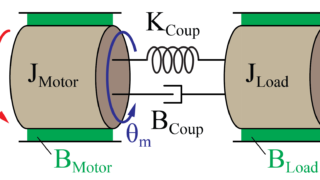
回転運動モデルの場合はこちら

運動方程式と伝達関数で２質量の回転運動モデルを表す 回転運動をするシステムについて、実際に２質量の回転運動モデルを用いながら、運動方程式の求め方から伝達関数で表す方法まで紹介してい...

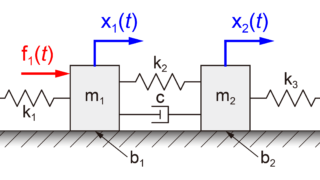
摩擦を含むモデルの場合はこちら

摩擦を含んだ2質量系の運動方程式を求める方法 システムの運動方程式や伝達関数の導出は、制御工学においての基本であり、とても重要です。 この運動方程式や伝達関数の...