
入力数と出力数が各々1つのシステムをSISI(Single Input Single Output)系と言います。
しかし、世の中には2つ以上の入力数や2つ以上の出力数をもつシステムも多くあります。
このようなシステムをMIMO(Multi Input Multi Output)系と言います。
今回は、今まで説明してきたSISO系の知識を使って、多入出力のMIMOシステムをどう扱うかについて説明します。
SISO系の伝達関数と状態空間モデル
おさらいです。
SISO系として、入力が\(u(t)\)で出力が\(y(t)\)の伝達関数は、
$$ Y(s) = G(s) U(s) $$
と表されます。
詳しくは、この記事を参考にして下さい。

SISO系を状態方程式(状態空間モデル)で表すと、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } + \boldsymbol{ B } u \\ y = \boldsymbol{ C } \boldsymbol{ x } + D u \end{array} \right. \end{eqnarray} $$
詳しくは、こちらの記事を参考にして下さい。
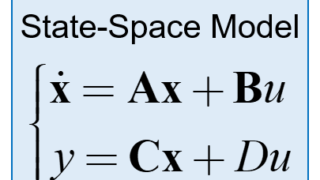
SISO系の場合、状態ベクトル\(x\)が\(n\)次元とすると、
Aは\(n \times n\)行列、Bは\(n \times 1\)ベクトル、Cは\(1 \times n\)ベクトル、Dはスカラ
となります。
MIMO系の伝達関数
\(l\)個の入力\(u(t)\)と\(m\)個の出力\(y(t)\)のMIMO系(多入力多出力系)のシステムを考えます。
\(l\)個の内\(i\)番目の入力\(u_i(t)\)と\(m\)個の出力の内\(j\)番目の出力\(y_j(t)\)の伝達関数が、
$$ Y_j(s) = G_{ji}(s) U_i(s) $$
で表されるとすると、システム全体の伝達関数は、
$$ \begin{bmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_m \end{bmatrix} = \begin{bmatrix} G_{11} & G_{12} & \cdots & G_{1l} \\ G_{21} & G_{22} & \cdots & G_{2l} \\ \vdots & \vdots & \ddots & \vdots \\ G_{m1} & G_{m2} & \cdots & G_{ml} \end{bmatrix} \begin{bmatrix} U_1 \\ U_2 \\ \vdots \\ U_l \end{bmatrix} $$
と表すことが出来ます。
このようなMIMO系の多入力と多出力の関係式を伝達関数行列と言います。
実際には、多入力・多出力であるが故の問題というのもあり得ます。
基本的なMIMO系のシステムでは伝達関数行列を用いて、各入力と各出力との個々の伝達関数の組み合わせで表現することが出来ます。
MIMO系の状態方程式(状態空間モデル)
基本的にはMIMOシステムの場合でもSISOシステムと同様に状態空間モデルを作成することが出来ます。
唯一の違いは、入力と出力に関する行列の次元数が入出力数によって変わります。
\(l\)個の入力\(u(t)\)と\(m\)個の出力\(y(t)\)のMIMO系(多入力多出力系)のシステムを考えます。
このMIMOシステムの状態空間モデルは、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } + \boldsymbol{ B } \boldsymbol{ u } \\ \boldsymbol{ y } = \boldsymbol{ C } \boldsymbol{ x } + \boldsymbol{ D } \boldsymbol{ u } \end{array} \right. \end{eqnarray} $$
と表すことが出来ます。
このようなMIMO系の多入力と多出力の関係式を状態方程式と言います。
MIMO系の場合、状態ベクトル\(x\)が\(n\)次元とすると、
Aは\(n \times n\)行列、Bは\(n \times l\)ベクトル、Cは\(m \times n\)ベクトル、Dは\(l \times m\)行列
となります。
まとめ
今回はMIMO系のシステムを伝達関数行列と状態方程式(状態空間モデル)で表す方法を紹介しました。
基本的には、SISO系が理解できていればMIMO系の理解は難しくないと思います。
次回はMIMO系システムの例を使って、実際に計算していきたいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
