台車型倒立振子の状態方程式を線形化する

今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。

前回までの記事では、台車型倒立振子システムの運動方程式から状態方程式を求める方法を紹介しました。

台車型倒立振子を制御するために状態方程式を求める台車の上に倒立振子が設置されているシステムを台車型倒立振子と言います。この台車型倒立振子を制御するために、システ...

今回の記事では、台車型倒立振子モデルを制御するために、非線形関数を含む状態方程式を線形化する方法を紹介します。

Contents

台車型倒立振子モデルと状態方程式
状態方程式の線形化
まとめ

台車型倒立振子モデルと状態方程式

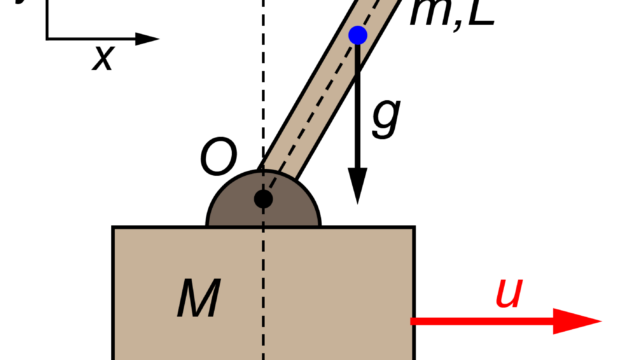
今回の記事では、下の図のように上向きの振り子（倒立振子）が台車の上に設置されているモデルを取り扱います。

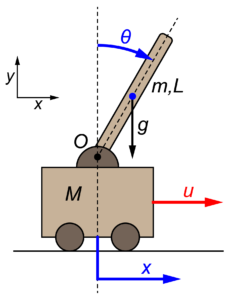
この台車型倒立振子モデルについて、台車の変位をx、棒振り子の角度をθと定義します。

このシステムの状態ベクトルXを

$$ \boldsymbol{ X } = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} x \\ \dot{x} \\ \theta \\ \dot{\theta} \end{bmatrix} $$

と定義すると、この台車型倒立振子システムの状態方程式は

$$ \begin{eqnarray} \boldsymbol{ \dot{X} } &=& \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} f_1(\boldsymbol{X} , u) \\ f_2(\boldsymbol{X} , u) \\ f_3(\boldsymbol{X} , u) \\ f_4(\boldsymbol{X} , u) \end{bmatrix} \\ &=& \begin{bmatrix} x_2 \\ \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ x_4 \\ \frac{\frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \end{bmatrix} \end{eqnarray} $$

のように表すことが出来ます。

詳しい算出方法は、こちらの記事を参考にしてください。

ここで、この状態方程式にはsin関数（$\sin(x_3)$）やcos関数（$\cos(x_3)$）などの非線形関数が含まれています。

さらに、状態変数同士の掛け算（$x_2 x_4$）や状態変数の2乗（${x_4}^2$）の項も存在します。

このような非線形関数を含む状態方程式のままでは、台車型倒立振子の制御が複雑になってしまいます。

そのため、この状態方程式を線形化して制御を簡単に行えるようにする方法を紹介します。

状態方程式の線形化

非線形関数f_iで表された状態方程式について

平衡点を見つける
非線形関数を偏微分する
平衡点を代入する

の3つのステップに沿って、線形化を行います。

詳しい線形化の手法については、こちらの記事を参考にしてください。

非線形システムを線形システムに変換する：制御工学入門　本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。 https://t...

平衡点を見つける

非線形関数によるシステムの状態方程式を線形化するために、台車型倒立振子モデルの平衡点$\boldsymbol{\bar{X}}$を見つけます。

平衡点とは、システムの状態Xが制止する点の事です。

平衡点の求め方についての詳細は、こちらの記事を参考にしてください。

非線形システムの振り子を線形化する：制御工学入門　本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。 https://t...

台車について

台車が制止する状態とは、台車が停止している場合です。

よって、この台車の平衡点は

$$ \bar{x}_2 = 0 $$

となります。

倒立振子について

実際には、非線形関数を時間微分して平衡点を求めるのですが、今回は倒立振子（棒振り子）のイメージから平衡点を求めます。

台車型倒立振子モデルの図から分かるように、棒振り子の状態（角度と角速度）が制止する点は、棒振り子が上向きに真っすぐ止まっている場合です。

よって、この倒立振子の平衡点は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \bar{x}_3 = 0 \\ \bar{x}_4 = 0 \end{array} \right. \end{eqnarray} $$

となります。

これらの平衡点$\boldsymbol{\bar{X}}$を次に求める非線形関数を偏微分した行列に代入して、システムの線形化を行います。

非線形関数を偏微分する

台車型倒立振子の状態方程式を示す非線形関数f_iを、状態ベクトルXの各要素x_iで偏微分して、状態方程式の線形化に必要となるDf/Dxを求めていきます。

この非線形関数を状態変数で偏微分したDf/Dxは

$$ \frac{D\boldsymbol{f}}{D\boldsymbol{x}} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \frac{\partial f_1}{\partial x_3} & \frac{\partial f_1}{\partial x_4} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \frac{\partial f_2}{\partial x_3} & \frac{\partial f_2}{\partial x_4} \\ \frac{\partial f_3}{\partial x_1} & \frac{\partial f_3}{\partial x_2} & \frac{\partial f_3}{\partial x_3} & \frac{\partial f_3}{\partial x_4} \\ \frac{\partial f_4}{\partial x_1} & \frac{\partial f_4}{\partial x_2} & \frac{\partial f_4}{\partial x_3} & \frac{\partial f_4}{\partial x_4} \end{bmatrix} $$

の式で表されます。

非線形関数f₁について

まず、簡単な非線形関数f₁とf₃から偏微分していきたいと思います。

非線形関数f₁

$$ f_1 = x_2 $$

について、各状態変数で偏微分すると

となります。

非線形関数f₃について

同様に、非線形関数f₃

$$ f_3 = x_4 $$

について、各状態変数で偏微分すると

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial f_3}{\partial x_1} = 0 \\ \frac{\partial f_3}{\partial x_2} = 0 \\ \frac{\partial f_3}{\partial x_3} = 0 \\ \frac{\partial f_3}{\partial x_4} = 1 \end{array} \right. \end{eqnarray} $$

となります。

非線形関数f₂について

続いて、複雑な非線形関数f₂とf₄を偏微分していきたいと思います。

非線形関数f₂

$$ f_2 = \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} $$

を、各状態変数で偏微分します。

まず、非線形関数f₂には状態変数x₁が含まれていないため、

$$ \frac{\partial f_2}{\partial x_1} = 0 $$

となります。

次に、非線形関数f₂の状態変数x₂についての偏微分を考えると、非線形関数f₂の分子の一か所のみに状態変数x₂が含まれているため、偏微分した結果は

$$ \frac{\partial f_2}{\partial x_2} = \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_4}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} $$

となります。

同様に、状態変数x₄についても、非線形関数f₂の分子の2か所のみに状態変数x₄が含まれているため

$$ \frac{\partial f_2}{\partial x_4} = \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 +\frac{1}{3} m L \sin(x_3) {x_4}}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} $$

のように偏微分することが出来ます。

最後に、状態変数x₃で非線形関数f₂の偏微分を行いますが、状態変数x₃は非線形関数f₂の分子と分母の両方に含まれています。

そのため、計算が多少複雑になりますが、焦らず考えれば解けるレベルだと思います。

非線形関数f₂を状態変数x₃で偏微分した結果は、

$$ \begin{eqnarray} \frac{\partial f_2}{\partial x_3} &=& \frac{-\frac{1}{4} m \cos^2(x_3) x_2 x_4 + \frac{1}{4} m \sin^2(x_3) x_2 x_4 +\frac{1}{6} m L \cos(x_3) {x_4}^2 – \frac{1}{4} m g \cos^2(x_3) + \frac{1}{4} m g \sin^2(x_3)}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ & & – \frac{\frac{1}{2} m \sin(x_3) \cos(x_3)}{\left( \frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3) \right)^2} \left( -\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u \right) \end{eqnarray} $$

と求めることが出来ます。

これらより、非線形関数f₂を各状態変数で偏微分した結果は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial f_2}{\partial x_1} &=& 0 \\ \frac{\partial f_2}{\partial x_2} &=& \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_4}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ \frac{\partial f_2}{\partial x_3} &=& \frac{-\frac{1}{4} m \cos^2(x_3) x_2 x_4 + \frac{1}{4} m \sin^2(x_3) x_2 x_4 +\frac{1}{6} m L \cos(x_3) {x_4}^2 – \frac{1}{4} m g \cos^2(x_3) + \frac{1}{4} m g \sin^2(x_3)}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ & & – \frac{\frac{1}{2} m \sin(x_3) \cos(x_3) \left( -\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u \right) }{\left( \frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3) \right)^2} \\ \frac{\partial f_2}{\partial x_4} &=& \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 +\frac{1}{3} m L \sin(x_3) {x_4}}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \end{array} \right. \end{eqnarray} $$

と算出することが出来ました。

非線形関数f₄について

非線形関数f₄

$$ f_4 = \frac{\frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} $$

についても、非線形関数f₂と同様に各状態変数に対する偏微分を求めていきます。

まず、非線形関数f₄には状態変数x₁が含まれていないため、

$$ \frac{\partial f_4}{\partial x_1} = 0 $$

となります。

次に、状態変数x₂とx₄は非線形関数f₄の分子のみに含まれているため、偏微分した結果は

$$ \frac{\partial f_4}{\partial x_2} = – \frac{\frac{1}{2} \left( M + m \right) \sin(x_3) x_4}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} $$

$$ \frac{\partial f_4}{\partial x_4} = \frac{\frac{1}{2} m L \sin(x_3) \cos(x_3) {x_4} – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} $$

と算出することが出来ます。

最後に、計算が複雑になりそうな状態変数x₃について非線形関数f₄の偏微分を行います。

非線形関数f₄を状態変数x₃で偏微分すると

$$ \begin{eqnarray} \frac{\partial f_4}{\partial x_3} &=& \frac{\frac{1}{4} m L \cos^2(x_3) {x_4}^2 – \frac{1}{4} m L \sin^2(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \cos(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \cos(x_3) – \frac{1}{2} \sin(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \\ & & + \frac{\frac{1}{2} m L \sin(x_3) \cos(x_3) \left( \frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u \right)}{\left( \frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L \right)^2} \end{eqnarray} $$

というように求めることが出来ました。

これらより、非線形関数f₄を各状態変数で偏微分した結果は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial f_4}{\partial x_1} &=& 0 \\ \frac{\partial f_4}{\partial x_2} &=& – \frac{\frac{1}{2} \left( M + m \right) \sin(x_3) x_4}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \\ \frac{\partial f_4}{\partial x_3} &=& \frac{\frac{1}{4} m L \cos^2(x_3) {x_4}^2 – \frac{1}{4} m L \sin^2(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \cos(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \cos(x_3) – \frac{1}{2} \sin(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \\ & & + \frac{\frac{1}{2} m L \sin(x_3) \cos(x_3) \left( \frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u \right)}{\left( \frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L \right)^2} \\ \frac{\partial f_4}{\partial x_4} &=& \frac{\frac{1}{2} m L \sin(x_3) \cos(x_3) {x_4} – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \end{array} \right. \end{eqnarray} $$

と算出することが出来ました。

このような計算を行うことで、台車型倒立振子の状態方程式を線形化するために必要となるDf/Dxを、状態方程式を示す非線形関数f_iを状態ベクトルXの各要素x_iで偏微分し求めることが出来ました。

平衡点を代入する

これまでに算出した平衡点を非線形関数の偏微分による行列に代入することで、台車型倒立振子システムの線形化を行います。

非線形関数の偏微分による行列

に、平衡点

$$ \begin{eqnarray} \left\{ \begin{array}{l} \bar{x}_2 = 0 \\ \bar{x}_3 = 0 \\ \bar{x}_4 = 0 \end{array} \right. \end{eqnarray} $$

を代入することで、台車型倒立振子システムの状態ベクトルXを用いて

$$ \dot{\boldsymbol{ X }} = \left. \frac{D\boldsymbol{f}}{D\boldsymbol{x}} \right|_{\boldsymbol{ X } =\boldsymbol{\bar{X}} } \boldsymbol{ X } $$

のように、線形化を行うことが出来ます。

非線形関数f₁とf₃の偏微分について

まず、非線形関数f₁とf₃については、偏微分をした後の式に状態変数が含まれていないため、平衡点を代入せずに

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial f_1}{\partial x_1} = 0 \\ \frac{\partial f_1}{\partial x_2} = 1 \\ \frac{\partial f_1}{\partial x_3} = 0 \\ \frac{\partial f_1}{\partial x_4} = 0 \end{array} \right. \\ \left\{ \begin{array}{l} \frac{\partial f_3}{\partial x_1} = 0 \\ \frac{\partial f_3}{\partial x_2} = 0 \\ \frac{\partial f_3}{\partial x_3} = 0 \\ \frac{\partial f_3}{\partial x_4} = 1 \end{array} \right. \end{eqnarray} $$

のように、偏微分をした後の式と同じになります。

非線形関数f₂の偏微分について

次に、非線形関数f₂の偏微分

には、偏微分をした後の式に状態変数が含まれているため、平衡点を代入していきます。

ここで、偏微分後の式に含まれるsin関数とcos関数は、変数の状態x₃が0なので

$$ \begin{eqnarray} \left\{ \begin{array}{l} \sin(x_3) = \sin(0) = 0 \\ \cos(x_3) = \cos(0) = 1 \end{array} \right. \end{eqnarray} $$

となります。

また、各式の分子に含まれるx₂とx₄の項について、状態x₂とx₄が0のため、その項も0になります。

よって、それぞれの式に平衡点を代入すると

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial f_2}{\partial x_1} &=& 0 \\ \frac{\partial f_2}{\partial x_2} &=& 0 \\ \frac{\partial f_2}{\partial x_3} &=& \frac{- \frac{1}{4} m g}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m} \\ \frac{\partial f_2}{\partial x_4} &=& 0 \end{array} \right. \end{eqnarray} $$

となります。

非線形関数f₄の偏微分について

同様に、非線形関数f₄の偏微分についても平衡点を代入することで、

$$ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial f_4}{\partial x_1} &=& 0 \\ \frac{\partial f_4}{\partial x_2} &=& 0 \\ \frac{\partial f_4}{\partial x_3} &=& \frac{- \frac{1}{2} \left( M + m \right) g}{\frac{1}{4} m L -\frac{1}{3} \left( M + m \right) L} \\ \frac{\partial f_4}{\partial x_4} &=& 0 \end{array} \right. \end{eqnarray} $$

と求めることが出来ます。

小まとめ

算出した平衡点を代入した偏微分を基に、状態方程式を線形化すると

$$ \dot{\boldsymbol{ X }} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{- \frac{1}{4} m g}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{- \frac{1}{2} \left( M + m \right) g}{\frac{1}{4} m L -\frac{1}{3} \left( M + m \right) L} & 0 \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{\frac{1}{3}}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m} \\ 0 \\ \frac{\frac{1}{2}}{\frac{1}{4} m L -\frac{1}{3} \left( M + m \right) L} \end{bmatrix} u $$

のように求めることが出来ました。

以上のような流れで、非線形システムである台車型倒立振子の状態方程式を線形化することが出来ました。