非線形システムの振り子を線形化する：制御工学入門

本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。

制御工学入門制御工学（Control Engineering）についての情報を紹介します。動的システムと制御方法世の中にあふれる動的...

前回の記事では、非線形システムを線形に変換する方法を紹介しました。

非線形システムを線形システムに変換する：制御工学入門　本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。 https://t...

今回の記事では、実際に非線形なシステムの例として振り子を用いて、非線形システムの線形化を行いたいと思います。

Contents

非線形システムを線形化する方法
振り子を非線形関数で表す
非線形システムの振り子を線形化する
まとめ

非線形システムを線形化する方法

前回のおさらいです。

非線形関数fで与えられる複雑な非線形システム

$$ \dot{\boldsymbol{ x }} = f \left( \boldsymbol{ x } \right) $$

を線形化し、

$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$

のような線形システムの形にして、制御しやすいように変換します。

非線形な関数で与えられた非線形システムを線形システムに変更する線形化は

平衡点を見つける
非線形関数を偏微分する
平衡点を代入する

の３つのステップで行います。

今回は、非線形システムの振り子を用いて、実際に線形化を行う流れを説明していきます。

振り子を非線形関数で表す

今回は、ダンパー付きの振り子を例に用いて、非線形システムの線形化を説明していきます。

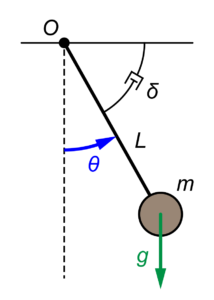
この振り子の運動方程式は、振り子の角度をθとすると

$$ \ddot{\theta} = – \frac{g}{L} \sin (\theta) – \delta \dot{\theta} $$

となります。

この運動方程式から状態方程式を求めます。

システムの状態xを

$$ \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} $$

と定義します。

この状態を用いて、非線形システムの振り子の非線形関数は

$$ \frac{d}{dt} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_2 \\ – \frac{g}{L} \sin (x_1) – \delta x_2 \end{bmatrix} $$

と表すことが出来ます。

この非線形な関係式を線形化して、振り子の状態方程式を求めていきます。

非線形システムの振り子を線形化する

実際に非線形関数fで表された非線形システムの振り子を

平衡点を見つける
非線形関数を偏微分する
平衡点を代入する

の３ステップに沿って、線形化していきます。

平衡点を見つける

非線形システムを線形システムに変換するために、振り子の平衡点$\boldsymbol{\bar{x}}$を見つけます。

システムの状態xが制止するためには、振り子の非線形関数

$$ \begin{eqnarray} \begin{array}{l} f_1 = \frac{d}{dt} x_1 = x_2 \\ f_2 = \frac{d}{dt} x_2 = – \frac{g}{L} \sin (x_1) – \delta x_2 \end{array} \end{eqnarray} $$

のそれぞれが0になるということです。

まず、1つ目の式f₁から

$$ \begin{eqnarray} \begin{array}{l} \frac{d}{dt} x_1 = x_2 = 0 \\ \quad \Rightarrow \ x_2 = 0 \end{array} \end{eqnarray} $$

とx₂求めることが出来ます。

このx₂＝0を2つ目の式f₂に代入すると

$$ \begin{eqnarray} \begin{array}{l} \frac{d}{dt} x_2 = – \frac{g}{L} \sin (x_1) – \delta x_2 = 0 \\ \quad \Rightarrow \ – \frac{g}{L} \sin (x_1) = 0 \\ \quad \Rightarrow \ x_1 = 0, \pi \end{array} \end{eqnarray} $$

とx₁を求めることが出来ました。

これより、振り子の平衡点$\boldsymbol{\bar{x}}$は

$$ \boldsymbol{\bar{x}} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} , \begin{bmatrix} \pi \\ 0 \end{bmatrix} $$

と求めることが出来ました。

ちなみに

先ほど非線形関数から平衡点を求めましたが、この平衡点は振り子をイメージすることで見つけることも出来ます。

まず、振り子の状態が制止するためには、角速度$\dot{\theta}$は0である必要があることは分かると思います。

そして、振り子の角度θは真っすぐ下向き（0°）か真っすぐ上向き（180°=π）である必要があることも、振り子の状態をイメージすれば分かると思います。

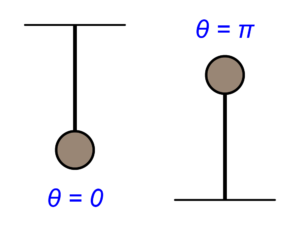
よって、与えられた振り子の平衡点$\boldsymbol{\bar{x}}$は

$$ \boldsymbol{\bar{x}} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} , \begin{bmatrix} \pi \\ 0 \end{bmatrix} $$

と、振り子の動作をイメージすることで求めることが出来ました。

今回用いた振り子のように、動作がシンプルなシステムはイメージのみで平衡点が分かりますが、複雑なシステムの場合は非線形関数から求めていくことが必要になります。

非線形関数を偏微分する

つぎに、振り子の運動を表す非線形関数fを偏微分して、状態方程式に必要な行列Df/Dx（ヤコビ行列）を求めます。

非線形関数（f₁、f₂）

$$ \begin{eqnarray} \begin{array}{l} \dot{x_1} = f_1 = x_2 \\ \dot{x_2} = f_2 = – \frac{g}{L} \sin (x_1) – \delta x_2 \end{array} \end{eqnarray} $$

をそれぞれ状態変数（x₁、x₂）で偏微分します。

非線形関数を状態変数で偏微分した結果は

$$ \begin{eqnarray} \frac{D\boldsymbol{f}}{D\boldsymbol{x}} &=& \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} \end{bmatrix} \\ &=& \begin{bmatrix} 0 & 1 \\ – \frac{g}{L} \cos (x_1) & – \delta \end{bmatrix} \end{eqnarray} $$

と求めることが出来ました。

平衡点を代入して線形化する

さいごに、偏微分により求めた行列Df/Dx

$$ \frac{D\boldsymbol{f}}{D\boldsymbol{x}} = \begin{bmatrix} 0 & 1 \\ – \frac{g}{L} \cos (x_1) & – \delta \end{bmatrix} $$

に平衡点$\boldsymbol{\bar{x}}$

$$ \boldsymbol{\bar{x}_{\textrm{down}}} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} , \ \boldsymbol{\bar{x}_{\textrm{up}}} = \begin{bmatrix} \pi \\ 0 \end{bmatrix} $$

をそれぞれ代入します。