詳細な根軌跡を描く方法：複素極や複素零点と軌跡との角度を求める

前回までの記事では、詳細な根軌跡を描くために必要となる情報として、実軸上から軌跡が分岐する点や軌跡と虚数軸との交点を求める方法を紹介しました。

詳細な根軌跡を描く方法：実軸上からの分岐点を求める 根軌跡を描くことが出来れば、複雑なフィードバックシステムの挙動を簡単に理解することが出来ます。 前回までの記事では...

詳細な根軌跡を描く方法：虚数軸との交点を求める 前回の記事では、詳細な根軌跡を描くために必要となる情報として、実軸上から軌跡が分岐する点を求める方法を紹介しました。 ht...

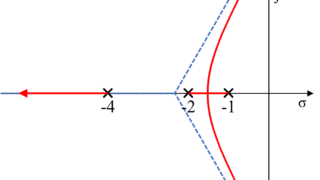
今回は、より詳細な根軌跡を書くための情報として、実軸上にない極や零点と軌跡とがなす角度を求める方法を紹介します。

詳細な根軌跡を描くための情報

より詳細な根軌跡を書くために必要となる情報として、

1. 実軸上からの分岐点
2. 虚軸との交点
3. 複素数点への入出力角 ← 今回

があります。

今回は、３つ目の複素数をもつ開ループ伝達関数の極や零点と軌跡とがなす入出力の角度を求める方法を紹介します。

フィードバックシステムと複素極

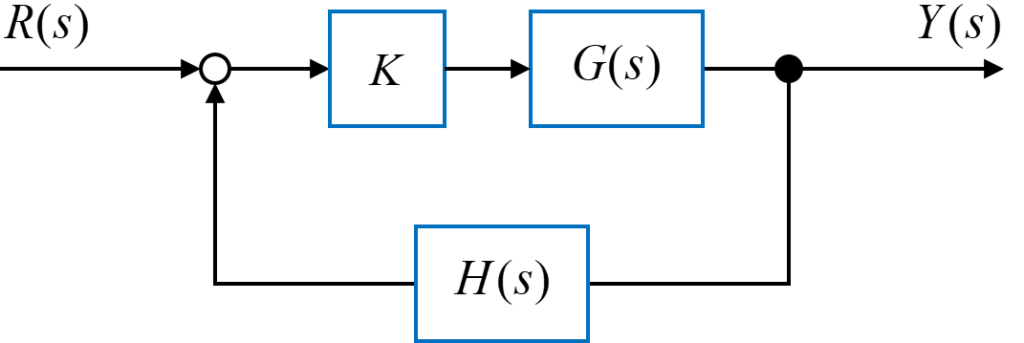
上図のようなフィードバックシステムの開ループ伝達関数が

$$ K G(s) H(s) = \frac{K (s+2)}{(s+3)(s^2+2s+2)} $$

で表されるシステムについて考えていきます。

このフィードバックシステムの開ループ伝達関数について、この伝達関数の零点は

$$ -2 $$

となり、極は

$$ -3, -1+j, -1-j $$

となります。

この開ループ伝達関数の極に含まれる複素極

$$ -1+j, -1-j $$

について、この2つの複素極を始点とした軌跡の角度を求めていきます。

複素極からの出力角を算出する

根軌跡の基本的なルールから、根軌跡上の点について

$$ \angle K G(s) H(s) = \left(2k+1\right) 180^{ \circ } $$

が成り立ちます。

この関係式を用いて複素極と軌跡との角度を求めます。

複素極\(-1+j\)から少しだけ（\(\varepsilon\)だけ）進んだ根軌跡上の点を考えます。

よって、この点と複素極\(-1+j\)とがなす角度\(\theta_1\)を先程のルールを用いて求めていきます。

この\(\varepsilon\)だけ移動した点と他の開ループ伝達関数の極（\(-1-j\)と\(-3\)）および零点（\(-2\)）がなす角度をそれぞれ\(\theta_2\)、\(\theta_3\)、\(\theta_4\)とします。

この\(\varepsilon\)だけ移動した点が根軌跡上に存在するために

$$ – \theta_1 – \theta_2 – \theta_3 + \theta_4 = \left(2k+1\right) 180^{ \circ } $$

が成り立つ必要があります。

これより、複素極\(-1+j\)を始点とした軌跡の角度\(\theta_1\)は

$$ \theta_1 = – \theta_2 – \theta_3 + \theta_4 – \left(2k+1\right) 180^{ \circ } $$

で求めることが出来ます。

実際に複素極と軌跡との角度を算出する

先程求めた関係式を用いて、実際に複素極\(-1+j\)を始点とした軌跡の角度\(\theta_1\)を求めていきます。

複素極\(-1+j\)から\(\varepsilon\)だけ移動した点と他の開ループ伝達関数の極および零点との角度は、\(\varepsilon\)が十分に小さい場合は複素極\(-1+j\)との角度と同じになります。

よって、開ループ伝達関数の極（\(-1-j\)と\(-3\)）および零点（\(-2\)）と複素極\(-1+j\)がなす角度（\(\theta_2\)、\(\theta_3\)、\(\theta_4\)）は

$$ \theta_2 = \arctan{\frac{2}{0}} = 90^{ \circ } $$

$$ \theta_3 = \arctan{\frac{1}{2}} = 26.6^{ \circ } $$

$$ \theta_4 = \arctan{\frac{1}{1}} = 45^{ \circ } $$

と求めることが出来ます。

これより、複素極\(-1+j\)を始点とした軌跡の角度\(\theta_1\)は

$$ \theta_1 = – 90^{ \circ } – 26.6^{ \circ } + 45^{ \circ } – \left(2k+1\right) 180^{ \circ } $$

$$ \Rightarrow \theta_1 = -251.6^{ \circ } = 108.4^{ \circ } $$

となる事が分かりました。

ここで、もう一つの複素極\(-1-j\)について根軌跡のルールより根軌跡は実軸に対して対象になるため、複素極\(-1-j\)を始点とした軌跡の角度\(\theta_2\)は

$$ \theta_2 = -108.4^{ \circ } $$

となります。

まとめ

今回は、より詳細な根軌跡を書くための情報として、実軸上にない複素極や複素零点と軌跡とがなす角度を求める方法を紹介しました。

次回は、具体的なフィードバックシステムに対して今まで紹介した根軌跡の特徴やルールを用いて、実際に根軌跡を書くことでシステムの挙動を理解する方法を紹介していきたいと思います。