本シリーズでは、制御工学で学ぶ基本的な知識から実際の応用例までを、なるべく分かりやすく解説しています。
前回までの記事では、非線形システムを線形化する方法と線形システムの安定性を確認する方法を紹介しました。
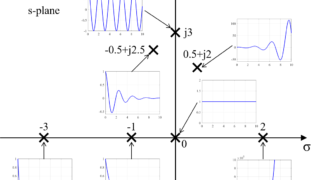
今回の記事では、例として非線形システムである振り子を用いて、実際に非線形システムを線形化した状態方程式から、システムの安定性を確認していきたいと思います。
振り子の線形化と状態方程式
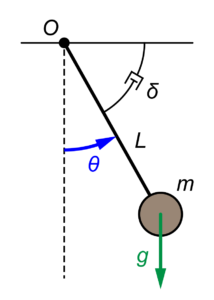
非線形システムであるダンパー付きの振り子の運動方程式
$$ \ddot{\theta} = – \frac{g}{L} \sin (\theta) – \delta \dot{\theta} $$
より、システムの状態xを
$$ \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} $$
と定義すると、この非線形システムの振り子は
$$ \frac{d}{dt} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_2 \\ – \frac{g}{L} \sin (x_1) – \delta x_2 \end{bmatrix} $$
という非線形関数で表すことが出来ます。
この非線形システムを
- 平衡点を見つける
- 非線形関数を偏微分する
- 平衡点を代入する
の３ステップを用いて、線形システムに変換します。
詳しくは、こちらの記事を参考にしてください。
線形化の３ステップを用いて平衡点周辺で線形システムに変換すると、振り子が真っすぐ下向きの場合は
$$ \dot{\boldsymbol{ x }} = \begin{bmatrix} 0 & 1 \\ – \frac{g}{L} & – \delta \end{bmatrix} \boldsymbol{ x } $$
となり、振り子が真っすぐ上向きの場合は
$$ \dot{\boldsymbol{ x }} = \begin{bmatrix} 0 & 1 \\ \frac{g}{L} & – \delta \end{bmatrix} \boldsymbol{ x } $$
というように線形化され、状態方程式で表すことが出来ます。
詳しくは、こちらの記事を参考にしてください。
安定性の確認方法
線形システムの常微分方程式（状態方程式）が
$$ \dot{\boldsymbol{ x }} = \boldsymbol{ A } \boldsymbol{ x } $$
と表されるとき、行列Aの固有値λを用いて、システムの安定性を確認することが出来ます。
行列Aの固有値λが複素数で表されるとき、全ての複素数λの実部が負（マイナス）であれば、システムは安定に動作します。
逆に、1つでも実部に正（プラス）が含まれている複素数λが存在した場合、そのシステムは不安定になります。
詳しくは、こちらの記事を参考にしてください。
ちなみに
行列Aの固有値λは
$$ \mathrm{det} \left( \boldsymbol{ A } – \lambda \boldsymbol{ I } \right) = 0 $$
という方程式を解くことで求められます。
実際の計算は後で紹介します。
振り子の安定性を確認
線形化したシステムの状態方程式
$$ \begin{eqnarray} \left\{ \begin{array}{ll} \dot{\boldsymbol{ x }} = \begin{bmatrix} 0 & 1 \\ – \frac{g}{L} & – \delta \end{bmatrix} \boldsymbol{ x } \ , & \mathrm{for} \ \boldsymbol{\bar{x}_{\textrm{down}}} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \\ \dot{\boldsymbol{ x }} = \begin{bmatrix} 0 & 1 \\ \frac{g}{L} & – \delta \end{bmatrix} \boldsymbol{ x } \ , & \mathrm{for} \ \boldsymbol{\bar{x}_{\textrm{up}}} = \begin{bmatrix} \pi \\ 0 \end{bmatrix} \end{array} \right. \end{eqnarray}$$
について、それぞれの平衡点での振り子の安定性を確認します。
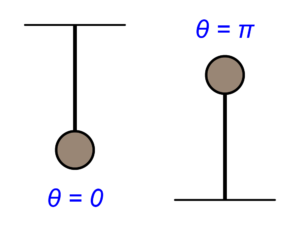
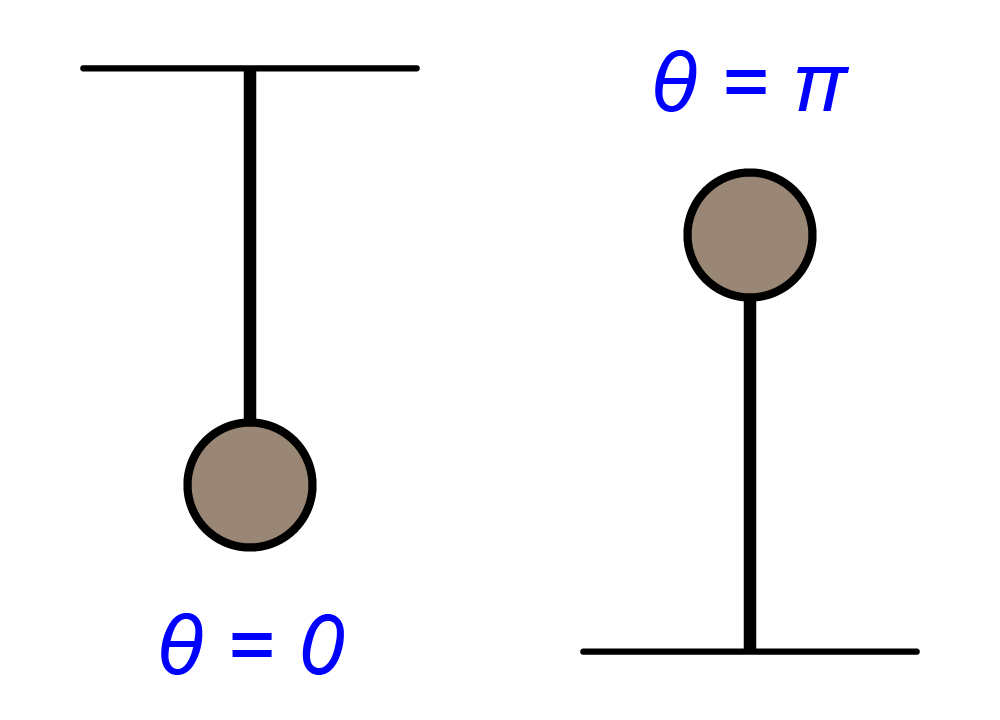
振り子が下向きの場合
まず、振り子が下向きの場合の行列
$$ \boldsymbol{A_{\textrm{down}}} = \begin{bmatrix} 0 & 1 \\ – \frac{g}{L} & – \delta \end{bmatrix} $$
について行列の固有値を求めて、安定性を確認します。
行列Aの固有値λを求める方程式
$$ \mathrm{det} \left( \boldsymbol{ A } – \lambda \boldsymbol{ I } \right) = 0 $$
より、行列Aを代入して固有値λを算出します。
$$ \begin{eqnarray} \mathrm{det} \left( \begin{bmatrix} 0 & 1 \\ – \frac{g}{L} & – \delta \end{bmatrix} – \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right) &=& 0 \\ \begin{vmatrix} – \lambda & 1 \\ – \frac{g}{L} & – \delta – \lambda \end{vmatrix} &=& 0 \\ \left(- \lambda \right) \left(- \delta – \lambda \right) – \left( 1 \right) \left(- \frac{g}{L} \right) &=& 0 \\ {\lambda}^2 + \delta \lambda + \frac{g}{L} &=& 0 \end{eqnarray} $$
この方程式を固有値λについて解くと
$$ \lambda = \frac{- \delta \pm \sqrt{{\delta}^2 – 4 \frac{g}{L}} }{2} $$
のように固有値λを求めることが出来ます。
ここで、それぞれのパラメータ（δ、g、L）の値は全て正（プラス）の値です。
よって、この固有値λについて解いた式のルート（√）部分の値は、δより小さくなります。
その結果、固有値λの実部の値はマイナスになります。
よって、固有値の実部がすべてマイナスなので、この振り子が下向きの場合のシステムの状態は安定となります。
振り子が上向きの場合
次に振り子が上向きの場合の行列
$$ \boldsymbol{\bar{x}_{\textrm{up}}} = \begin{bmatrix} \pi \\ 0 \end{bmatrix} $$
について、同様に固有値λを求め、安定性を確認します。
行列Aより固有値λの方程式を求めると
$$ \begin{eqnarray} \mathrm{det} \left( \begin{bmatrix} 0 & 1 \\ \frac{g}{L} & – \delta \end{bmatrix} – \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right) &=& 0 \\ \begin{vmatrix} – \lambda & 1 \\ \frac{g}{L} & – \delta – \lambda \end{vmatrix} &=& 0 \\ \left(- \lambda \right) \left(- \delta – \lambda \right) – \left( 1 \right) \left(\frac{g}{L} \right) &=& 0 \\ {\lambda}^2 + \delta \lambda – \frac{g}{L} &=& 0 \end{eqnarray} $$
となります。
そして、この方程式を解くことで
$$ \lambda = \frac{- \delta \pm \sqrt{{\delta}^2 + 4 \frac{g}{L}} }{2} $$
と、固有値λを求めることが出来ました。
ここで、それぞれのパラメータ（δ、g、L）の値は全て正（プラス）の値なので、固有値λについて解いた式のルート（√）部分の値は、δより大きくなります。
よって、固有値λの実部の値がプラスになる解が存在することになります。
その結果、実部が正（＋）の固有値λが含まれているため、振り子が上向きの状態のシステムは不安定ということが分かりました。
小まとめ
この安定性についての結果は、実際に振り子をイメージしてもらえば分かると思います。
振り子が下向きは、徐々に振り子の揺れ（振れ幅）が小さくなり、最後には下向きに制止することが想像できると思います。
そして、振り子が上向きの場合は、ちょっとの角度のズレにより、振り子がぐるっと下方向に回転し、再び振り子が上向きになり制止する事はありません。
今回の計算により求めた振り子の安定性と、今イメージしてもらった振り子の動作の様子は同じになることが分かると思います。
まとめ
今回は、非線形システムの振り子を線形化した状態方程式から、線形システムの安定性を確認する方法を紹介しました。
今回のような手法を用いることで、非線形システムの運動方程式から線形システムを求め、その安定性を知ることが出来ます。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
はじめまして。そもそも外力が働くこの振り子が非線形システムであることの証明ってできますでしょうか？
ご質問ありがとうございます。
非線形システムとは、sinやcosなどの非線形成分を含んでいるシステムの事を指します。
本記事の振り子の運動は、記事内で紹介した運動方程式を見ると分かるように非線形成分のsin(θ)を含んでいます。
そのため、この振り子は非線形システムであると言えます。
参考になれば幸いです。