倒立振子が台車の上に乗っているシステムを台車型倒立振子と言います。
この台車型倒立振子を制御する際には運動方程式を求める必要があります。
しかし、この台車型倒立振子のシステムは単純ではなく、運動方程式は複雑になります。
そのため、運動方程式の求め方が分からない方もいると思います。
今回の記事では、台車型倒立振子の運動方程式とラグランジュ方程式を用いた求め方を紹介します。
2019/7/6 追記
棒の回転エネルギーの算出方法が間違っていたため、修正いたしました。
台車型倒立振子とは
台車型倒立振子とは、下の図のように倒立振子が台車の上に設置されたモデルです。
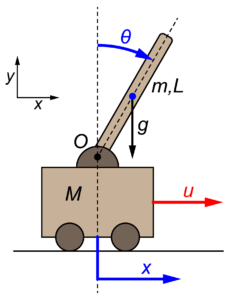
倒立振子とは、支点よりも重心が上(高い位置)にある振り子のことです。
今回の記事では、質量mで長さLの棒状の振り子を取り扱います。
支点O(黒丸)は棒の下側の端にあり、重心(青丸)が棒の中心位置にあるため、この振り子は倒立振子になります。
この倒立振子の支点Oを質量Mの台車の上に設置したモデルである台車型倒立振子を取り扱います。
この台車型倒立振子に対して、台車の位置をxとし棒振り子の傾きをθとします。
また、台車にかかる力をuと定義します。
このときの台車型倒立振子の運動方程式は
$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( M + m \right) \ddot{x} + \frac{1}{2} m L \cos (\theta) \ddot{\theta} -\frac{1}{2} m L \sin (\theta) \dot{\theta}^2 = u \\ \frac{1}{2} m L \cos (\theta) \ddot{x} – \frac{1}{2} m L \sin (\theta) \dot{x} \dot{\theta} + \frac{1}{3} m L^2 \ddot{\theta} – \frac{1}{2} m g L \sin (\theta) = 0 \end{array} \right. \end{eqnarray} $$
と表すことが出来ます。
この台車型倒立振子の運動方程式の求め方については、下記で説明していきます。
ラグランジュ方程式と運動方程式
今回は、システムの運動方程式を求めるためにラグランジュ方程式を用います。
ラグランジュ方程式を用いて求めた運動方程式の一般式は
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = 0 $$
と表されます。
ここで、KEは運動エネルギーで、PEは位置エネルギーを示しています。
また、xはシステムの変数を表しています。
ラグランジュ方程式について詳しくは、こちらの記事を参考にしてください。
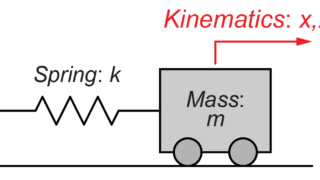
もし、システム内に外力Fが存在する場合は
$$ \frac{d}{dt} \left( \frac{\partial}{\partial \dot{x}} KE \right) + \frac{\partial}{\partial x} PE = F $$
のように、式の右辺に加わる外力が追加されます。
ラグランジュ方程式を用いて運動方程式を求めるために、システムの運動エネルギー(KE)と位置エネルギー(PE)を算出していきます。
運動エネルギー(KE)
ラグランジュ方程式を用いて運動方程式を求めるために、まずシステムの運動エネルギー(KE)を算出していきます。
今回の記事で取り扱う台車型倒立振子のシステムには、台車と振り子という2つの物体の運動が含まれています。
また、振り子については支点を中心に回転による運動もあります。
よって、
- 台車の移動による運動エネルギー:KEM
- 振り子の移動による運動エネルギー:KEm
- 振り子の回転による運動エネルギー:KEI
をそれぞれ求めて、足し合わせることでシステム全体の運動エネルギーを求めていきます。
台車の移動による運動エネルギー:KEM
台車の位置を\(x\)とした時、台車の速度は\(\dot{x}\)と表すことが出来ます。
よって、質量Mの台車が速度\(\dot{x}\)移動した場合の運動エネルギーKEMは
$$ {KE}_M = \frac{1}{2} M \dot{x}^2 $$
と求めることが出来ます。
振り子の移動による運動エネルギー:KEm
台車の運動エネルギーKEMと同様に、振り子の移動による運動エネルギーKEmを求めていきます。
今回の台車型倒立振子では、振り子は台車の上に乗っています。
そのため振り子の速度を求めるためには、振り子自体の速度に加えて台車の速度を考慮する必要があります。
まず振り子単体の速度を求めます。
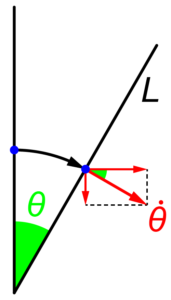
振り子の回転角度を\(\theta\)として、回転の速度を\(\dot{\theta}\)とします。
この時の回転速度\(\dot{\theta}\)と支点Oから重心までの距離L/2から、振り子単体の速度はX軸方向、Y軸方向それぞれ
$$ \frac{L}{2} \cos (\theta) \dot{\theta} \ , \ – \frac{L}{2} \sin (\theta) \dot{\theta} $$
と求めることが出来ます。
振り子のX軸方向の速度\(\dot{x}_{m,x}\)は、振り子の速度に台車の速度\(\dot{x}\)を加えて
$$ \dot{x}_{m,x} = \dot{x} + \frac{L}{2} \cos (\theta) \dot{\theta} $$
となります。
また、Y軸方向の振り子の速度\(\dot{x}_{m,y}\)は、台車の速度が影響しないため
$$ \dot{x}_{m,y} = – \frac{L}{2} \sin (\theta) \dot{\theta} $$
となります。
よって、質量mの振り子の速度\(\dot{x}_m\)は
$$ \begin{eqnarray} \dot{x}_m &=& \sqrt{{\dot{x}_{m,x}}^2+{\dot{x}_{m,y}}^2} \\ &=& \sqrt{\left( \dot{x} + \frac{L}{2} \cos (\theta) \dot{\theta} \right)^2 + \left( – \frac{L}{2} \sin (\theta) \dot{\theta} \right)^2 } \end{eqnarray} $$
と求めることが出来ます。
これより、質量mの振り子の移動による運動エネルギーKEmは
$$ \begin{eqnarray} {KE}_m &=& \frac{1}{2} m {\dot{x}_m}^2 \\ &=& \frac{1}{2} m \left[ \left( \dot{x} + \frac{L}{2} \cos (\theta) \dot{\theta} \right)^2 + \left( – \frac{L}{2} \sin (\theta) \dot{\theta} \right)^2 \right] \\ &=& \frac{1}{2} m \left[ \dot{x}^2 + 2 \frac{L}{2} \cos (\theta) \dot{x} \dot{\theta} + \left(\frac{L}{2}\right)^2 \cos^2 (\theta) \dot{\theta}^2 + \left(\frac{L}{2}\right)^2 \sin^2 (\theta) \dot{\theta}^2 \right] \\ &=& \frac{1}{2} m \left[ \dot{x}^2 + L \cos (\theta) \dot{x} \dot{\theta} + \frac{L^2}{4} \dot{\theta}^2 \left( \cos^2 (\theta) + \sin^2 (\theta) \right) \right] \\ &=& \frac{1}{2} m \left[ \dot{x}^2 + L \cos (\theta) \dot{x} \dot{\theta} + \frac{L^2}{4} \dot{\theta}^2 \right] \end{eqnarray} $$
と表すことが出来ます。
振り子の回転による運動エネルギー:KEI
最後に振り子の回転による運動エネルギーKEIを求めていきます。
先の項で、振り子の移動による運動エネルギーKEmを重心周りで算出したため、振り子の回転による運動エネルギーKEIについても重心周りについて算出します。
重心周りに対する一様な棒の慣性モーメントIOは
$$ I_O = \frac{1}{12} m L^2 $$
と算出することが出来ます。
これより、振り子の回転による運動エネルギーKEIは、慣性モーメントIOと回転速度\(\dot{\theta}\)を用いて
$$ \begin{eqnarray} {KE}_I &=& \frac{1}{2} I_O \dot{\theta}^2 \\ &=& \frac{1}{2} \left[ \frac{1}{12} m L^2 \right] \dot{\theta}^2 \end{eqnarray} $$
と求めることが出来ます。
全体の運動エネルギー:KE
これまでに求めた3つの運動エネルギー(KEM、KEm、KEI)を足し合わせることで、台車型倒立振子の運動エネルギー(KE)を求めることが出来ます。
よって、台車型倒立振子の運動エネルギーKEは
$$ \begin{eqnarray} KE &=& {KE}_M + {KE}_m + {KE}_I \\ &=& \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left[ \dot{x}^2 + L \cos (\theta) \dot{x} \dot{\theta} + \frac{L^2}{4} \dot{\theta}^2 \right] + \frac{1}{2} \left[ \frac{1}{12} m L^2 \right] \dot{\theta}^2 \end{eqnarray} $$
となります。
位置エネルギー(PE)
同様に、ラグランジュ方程式を用いて運動方程式を求めるために、システムの位置エネルギー(PE)を求めていきます。
今回の台車型倒立振子モデルでは、台車は常に地面(高さが0)にいるため、位置エネルギーはありません。
よって、棒振り子の位置エネルギーが台車型倒立振子の位置エネルギーになります。
全体の位置エネルギー:PE
振り子の角度がθの時の重心の高さhは
$$ h = \frac{L}{2} \cos (\theta) $$
と三角関数を使って求めることが出来ます。
これより、台車型倒立振子の位置エネルギーPEは
$$ \begin{eqnarray} PE &=& m g h \\ &=& m g \left( \frac{L}{2} \cos (\theta) \right) \\ &=& \frac{m g L}{2} \cos (\theta) \end{eqnarray}$$
となります。
まとめ
今回の記事では、台車型倒立振子の運動方程式を紹介しました。
また、実際に運動方程式を求めるためにラグランジュ方程式を用いた手法を紹介し、台車型倒立振子の運動エネルギーと位置エネルギーの算出の方法を紹介しました。
次回の記事では、今回の記事で求めた運動エネルギーと位置エネルギーをラグランジュ方程式に代入して、実際に台車型倒立振子の運動方程式を求める方法を紹介します。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+

棒の回転の運動エネルギーが誤っていると思います。一方で重心の運動エネルギーを1項起こしているのですから、回転の運動エネルギーは重心まわりの回転について
E_I = 1/2・1/12・mL^2θ’^2
とすべきです。
x’=0 の特別な場合について考えるとはっきりします。
E = E_m + E_I = 1/2(1/4+1/3)mL^2θ’^2 = 1/2・7/12・mL^2θ’^2
これは明らかにおかしいです。
E = E_m + E_I = 1/2(1/4+1/12)mL^2θ’^2 = 1/2・1/3・mL^2θ’^2
こちらがまさに軸まわりの回転のエネルギーを表しており、整合します。
ご指摘ありがとうございます。
ご指摘いただいた通り、棒の回転エネルギーについて重心周りで算出すべきところを端点周りで算出していました。
重心周りで算出した式に修正いたしました。
情報を発信する者として、以後正確な情報をお届けできるように気を付けます。
今後ともどうぞよろしくお願いします。
棒の慣性モーメントですが,重心周りではなく,端点周りに直す必要はないのでしょうか?
ご質問ありがとうございます。
本記事で紹介している計算方法では、振り子のエネルギーを考える際に振り子の重心を基準に考えています。
振り子の運動エネルギーを求める際にも、振り子の重心の移動について考えて、計算を行っています。
そのため、振り子の慣性モーメントについても振り子の重心で考えるため、端点周りに直す必要はありません。
参考になれば幸いです。
台車と床の間に摩擦係数kで摩擦力が発生する場合、台車の移動による運動エネルギーKE_Mの式の右辺の第二項として-kmgxが必要になりますか?
ご質問ありがとうございます。
摩擦により生じるエネルギーに関しては、運動エネルギーとは別に取り扱う必要があります。
そのため、運動エネルギーの式に組み込んではいけません。
摩擦力については、散逸関数を用いて別に定義して取り扱います。
形は異なりますが、こちらの記事で散逸関数について触れています。
https://tajimarobotics.com/equation-of-motion-damped-physical-pendulum-example/
参考になれば幸いです。