摩擦を含んだ2質量系の伝達関数を求める：運動方程式のラプラス変換から導出

制御工学において、運動方程式や伝達関数の導出はとても重要な項目です。

これら運動方程式と伝達関数の導出方法を身に着けるためには、様々なパターンのシステムを取り扱うことが大事だと考えています。

前回の記事では、摩擦を含む2自由度システムの運動方程式を導出する流れを紹介しました。

摩擦を含んだ2質量系の運動方程式を求める方法システムの運動方程式や伝達関数の導出は、制御工学においての基本であり、とても重要です。この運動方程式や伝達関数の...

今回の記事では、摩擦を含む2質量系の伝達関数を求める方法を紹介します。

Contents

取り扱う2自由度システム
運動方程式をラプラス変換
伝達関数の算出
- 質量1について
- 質量2について
まとめ

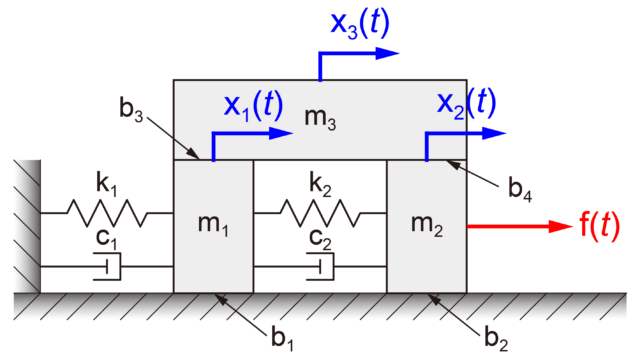
取り扱う2自由度システム

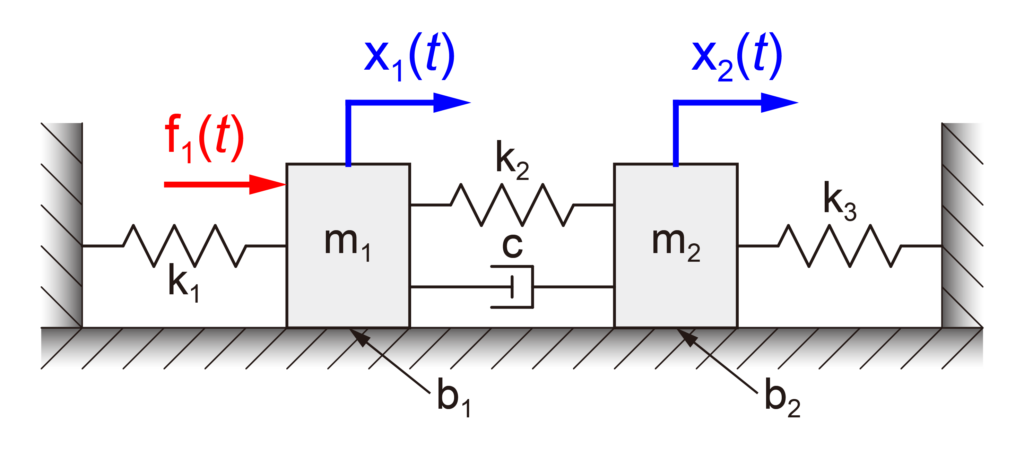
この記事では、上の図のような2自由度の質量-ばね-ダンパーシステムを取り扱います。

前回の記事にて、運動方程式は下記のように算出しました。

$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 \ddot{x}_1(t) + \left( b_1 + c \right) \dot{x}_1(t) + \left( k_1 + k_2 \right) x_1(t) – c \dot{x}_2(t) – k_2 x_2(t) &=& f_1(t) \\ m_2 \ddot{x}_2(t) + \left( b_2 + c \right) \dot{x}_2(t) + \left( k_2 + k_3 \right) x_2(t) – c \dot{x}_1(t) – k_2 x_1(t) &=& 0 \end{array} \right. \end{eqnarray} $$

今回の記事では、この運動方程式から伝達関数を求めていきたいと思います。

運動方程式をラプラス変換

まず始めに、時間領域tで表されている運動方程式を周波数領域sで表すためにラプラス変換を行います。

時間tについての関数である運動方程式

をラプラス変換により、周波数sについての式で表すと

$$ \begin{eqnarray} \left\{ \begin{array}{l} m_1 s^2 X_1(s) + \left( b_1 + c \right) s X_1(s) + \left( k_1 + k_2 \right) X_1(s) – c s X_2(s) – k_2 X_2(s) &=& F_1(s) \\ m_2 s^2 X_2(s) + \left( b_2 + c \right) s X_2(s) + \left( k_2 + k_3 \right) X_2(s) – c s X_1(s) – k_2 X_1(s) &=& 0 \end{array} \right. \end{eqnarray} $$

となります。

ラプラス変換した式を整理すると、

$$ \begin{eqnarray} \left\{ \begin{array}{l} \left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right) X_1(s) – \left( c s + k_2 \right) X_2(s) &=& F_1(s) \\ – \left( c s + k_2 \right) X_1(s) + \left( m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right) \right) X_2(s) &=& 0 \end{array} \right. \end{eqnarray} $$

となり、運動方程式を時間領域tから周波数領域sに変換することが出来ました。

ラプラス変換の基本については、こちらの記事を参考にしてください。

ラプラス変換を用いてシステムを伝達関数で表す前回は、線形時不変システム（LTIシステム）を説明しました。ただ、動的システムに対してLTIシステムのモデルを用いると計...

伝達関数の算出

それでは、先ほどラプラス変換により周波数領域sで表された運動方程式より、伝達関数を算出します。

今回は、力F₁に対する各質量の位置（X₁とX₂）について伝達関数で表したいと思います。

質量1について

最初に、入力として力F₁(s)が与えられた時の質量m₁の位置X₁(s)を出力とする伝達関数G₁(s)

$$ G_1(s) = \frac{X_1(s)}{F_1(s)} $$

を求めていきます。

ラプラス変換後の運動方程式の第2式

$$ – \left( c s + k_2 \right) X_1(s) + \left( m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right) \right) X_2(s) = 0 $$

より、質量m₂の位置X₂(s)を質量m₁の位置X₁(s)を用いて表すと

$$ X_2(s) = \frac{c s + k_2}{m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right)} X_1(s) $$

となります。

これをラプラス変換後の運動方程式の第1式

$$ \left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right) X_1(s) – \left( c s + k_2 \right) X_2(s) = F_1(s) $$

に代入すると

$$ \left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right) X_1(s) – \left( c s + k_2 \right) \frac{c s + k_2}{m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right)} X_1(s) = F_1(s) $$

となります。

この式を整理すると、力F₁(s)に対する質量m₁の位置X₁(s)を表す伝達関数G₁(s)は、

$$ G_1(s) = \frac{X_1(s)}{F_1(s)} = \frac{m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right)}{\left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right)\left( m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right) \right) – \left( c s + k_2 \right)^2} $$

と求めることが出来ました。

質量2について

同様に、入力として力F₁(s)が与えられた時の質量m₂の位置X₂(s)を出力とする伝達関数G₂(s)

$$ G_2(s) = \frac{X_2(s)}{F_1(s)} $$

を求めていきます。

ラプラス変換後の運動方程式の第2式

$$ – \left( c s + k_2 \right) X_1(s) + \left( m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right) \right) X_2(s) = 0 $$

について、今度は質量m₁の位置X₁(s)を質量m₂の位置X₂(s)を用いて表すと

$$ X_1(s) = \frac{m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right)}{c s + k_2} X_2(s) $$

となります。

この式をラプラス変換後の運動方程式の第1式

$$ \left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right) X_1(s) – \left( c s + k_2 \right) X_2(s) = F_1(s) $$

に代入することで

$$ \left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right) \frac{m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right)}{c s + k_2} X_2(s) – \left( c s + k_2 \right) X_2(s) = F_1(s) $$

が得られます。

これより、力F₁(s)に対する質量m₂の位置X₂(s)を表す伝達関数G₂(s)は、

$$ \frac{X_2(s)}{F_1(s)} = \frac{c s + k_2}{\left( m_1 s^2 + \left( b_1 + c \right) s + \left( k_1 + k_2 \right) \right)\left( m_2 s^2 + \left( b_2 + c \right) s + \left( k_2 + k_3 \right) \right) – \left( c s + k_2 \right)^2} $$

となることが分かりました。