Bスプライン曲線で離散点を補間するプログラムを作成してみた

Bスプライン曲線を用いることで、離散点を補間してスムーズな曲線を書くこと出来ます。

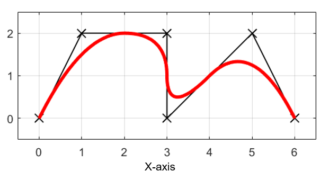
実際にBスプライン曲線で指令値を補間してみた：ロボットの軌跡生成これまでのシリーズ記事では、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間する方法を紹介しています。 ...

このBスプライン曲線を表す式は比較的シンプルなので、コンピュータグラフィックスの分野などで広く使われています。

しかし、実際にプログラムを作成するとなると、どうでしょう？難しく感じる方も多いと思います。

今回の記事では、実際に作成したBスプライン曲線のプログラムを見ながら、離散点をBスプライン曲線により補間する方法を紹介していきたいと思います。

Contents

Bスプライン曲線とは
Bスプライン曲線のプログラム
プログラム内のBスプライン曲線の式
- Bスプライン曲線の基本式
- Bスプライン基底関数
まとめ

Bスプライン曲線とは

Bスプライン曲線（またはB-スプライン曲線）とは、制御点とノットベクトルより定義される滑らかな曲線です。

このBスプライン曲線を用いて、離散的な指令点を滑らかな曲線に変換して補間することをBスプライン補間と言います。

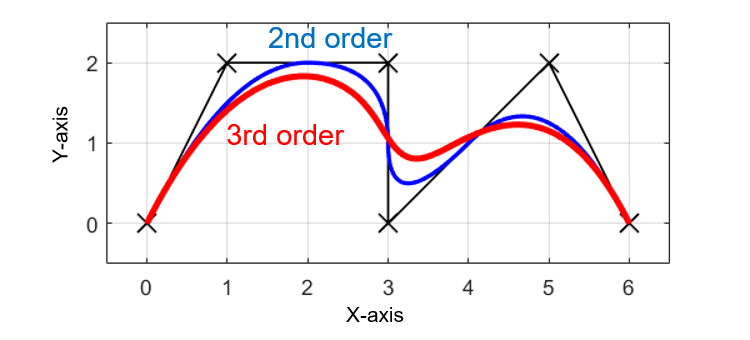
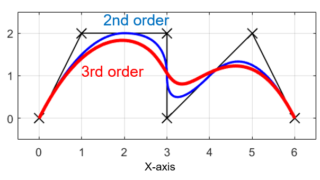
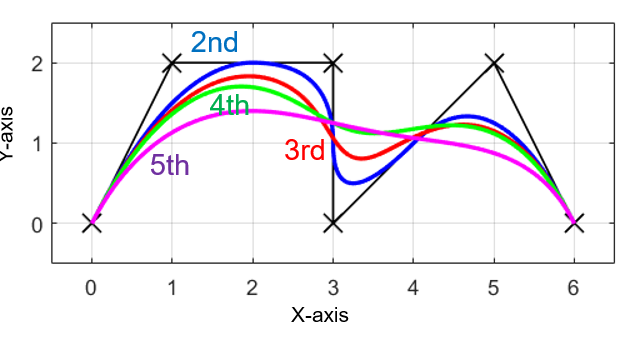
離散的な指令点（黒✕）を2次（青線）と3次（赤線）のBスプライン曲線で補間した結果は上の図のようになります。

以下に、Bスプライン曲線を書くために必要となる式を紹介していきます。

Bスプライン曲線の基本式

Bスプライン曲線の基本式は

$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(u) \ , \quad u \in [u_0,u_{m-1}] $$

のように、制御点P_iとBスプライン基底関数b_i,n、そしてノットベクトルuを用いて表されます。

Bスプライン基底関数

Bスプライン基底関数は

$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 \\ b_{j,k}(u) = \frac{u-u_j}{u_{j+k}-u_j} b_{j,k-1}(u) + \frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(u) \ , \quad j=0,1,\cdots, m-k-2 \end{array} \end{eqnarray} $$

とノットベクトルuから定義することが出来ます。

ノットベクトル

今回のBスプライン曲線を用いた補間で用いるノットベクトルは、開一様ノットベクトルを用います。

ノットベクトルは、指令点の数pやBスプライン曲線の次数nによって決定することが出来ます。

指令点の数pが6点、Bスプライン曲線の次数nが3次の場合の開一様ノットベクトルは、

$$ \boldsymbol{u} = [0,0,0,0,0.333,0.667,1,1,1,1] $$

と定義されます。

Bスプライン曲線についての詳細については、こちらの記事を参考にしてください。

Bスプライン曲線を使ってロボットの軌跡生成をしてみよう！（その１）前回の記事では、Bスプライン曲線とベジエ曲線について、それぞれの特徴と関係性を説明し、ロボットの軌跡生成への応用例を紹介しました...

Bスプライン曲線のプログラム

先程紹介したB-スプライン曲線の基本式をベースにMATLABで作成した、離散的な指令点から滑らかな曲線に変換するためのB-スプライン補間のプログラムは以下のようになります。

メインプログラム

制御点の定義からBスプライン曲線の作成を行うメインプログラム：

% Control Points (X-Y)
P = [ 
    0.0, 0.0;
    1.0, 2.0;
    3.0, 2.0;
    3.0, 0.0;
    5.0, 2.0;
    6.0, 0.0;
    ];

p = length(P);  % Number of Control Ponits
n = 3;          % Degree of B-Spline
m = p + n + 1;  % Number of Knots in Knot Vector
    
% Define Knot Vector
u = OpenUniformKnotVector(m,n);

t = 0:0.01:u(end);

% Calculate B-spline Curve
S = zeros(length(t),2);
S(1,:) = P(1,:);
for i = 2:length(t)
    for j =1:p
        b = BasisFunction(u,j,n,t(i));  
        S(i,:) = S(i,:) + P(j,:)*b;
    end
end

return

また、このメインのプログラム内では

OpenUniformKnotVector（開一様ノットベクトルを作成）
BasisFunction（Bスプライン基底関数を算出）

の2つの関数を定義して使用しています。

この2つの関数は以下のように作成しました。

開一様ノットベクトル作成用関数

開一様ノットベクトルを作成するための関数：OpenUniformKnotVector

% u : Knot Vector
% m : Number of Knots in Knot Vector
% n : Degree of B-Spline
function u = OpenUniformKnotVector(m,n)
    u = zeros(1,m);
    for i = 1:1:m
          if i < n+1 
              u(i) = 0;
          elseif i > m - (n + 1) 
              u(i) = m - 1 - 2 * n;
          else
              u(i) = i - n - 1;
          end
    end
    u = u/u(end);      
end

Bスプライン基底関数算出用関数

Bスプライン基底関数を算出するための関数：BasisFunction

% u : Knot Vector
% j : j-th Control Ponit
% k : k-th Basis Function <-- n-th B-Spline
% t : Time
function var = BasisFunction(u,j,k,t)   
    w1 = 0.0;
    w2 = 0.0;
    
    if k == 0 
        if u(j) < t && t <= u(j+1)
            var = 1.0;
        else
            var = 0.0;
        end
    else
        if (u(j+k+1)-u(j+1)) ~= 0  
            w1 = BasisFunction(u,j+1,k-1,t) * (u(j+k+1) - t)/(u(j+k+1)-u(j+1));
        end
        if (u(j+k)-u(j)) ~= 0  
            w2 = BasisFunction(u,j,k-1,t) * (t - u(j))/(u(j+k) - u(j));
        end
        var = w1 + w2;
    end  
end

プログラム内のBスプライン曲線の式

実際にプログラムを作成するにあたり変更した、Bスプライン曲線の式を説明します。

Bスプライン曲線の基本式

過去の記事や本記事の最初に紹介したBスプライン曲線の基本式では

$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(u) \ , \quad u \in [u_0,u_{m-1}] $$

のようにBスプライン曲線の変数として”u“を用いていました。

しかし、プログラムを作成時に変数名を定義する際に、ノットベクトルの”u“と変数の”u“の違いが分かりにくいため、今回は”u“の代わりに”t“を用いてプログラムの作成を行いました。

変数名として”t“を選んだ理由は、”time“（時間）の頭文字だからです。

よって、今回はBスプライン曲線の基本式として

$$ \boldsymbol{ S }(t) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(t) \ , \quad t \in [u_0,u_{m-1}] $$

を用いてプログラムの作成を行います。

Bスプライン基底関数

同様に、Bスプライン基底関数についても、変数”u“の代わりに”t“を用いて

$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(t) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \lt t \leq u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 \\ b_{j,k}(t) = \frac{t-u_j}{u_{j+k}-u_j} b_{j,k-1}(t) + \frac{u_{j+k+1}-t}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(t) \ , \quad j=0,1,\cdots, m-k-2 \end{array} \end{eqnarray} $$

の定義式を用いてプログラムの作成を行いました。

また、Bスプライン基底関数b_j,0の式について、値が1となる範囲を

$$ u_j \leq u \lt u_{j+1} \Rightarrow u_j \lt t \leq u_{j+1} $$

のように不等号を変更しています。

この変更の理由は、Bスプライン曲線による離散的な指令点の補間を、ロボットの軌跡生成により対応させるためです。

ロボットの軌跡を生成する際に、基本的に時刻t=0でのロボットの位置は一番初めの指令値の位置になります。

そのため、時刻t=0でのBスプライン曲線による補間後の状態（X、Y位置）は、指令値の1つ目の状態（X、Y位置）を代入します。

そして、その後の値に対してBスプライン補間を行い、離散的な指令値から滑らかな曲線を生成します。