これまでのシリーズ記事では、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間する方法を紹介しています。
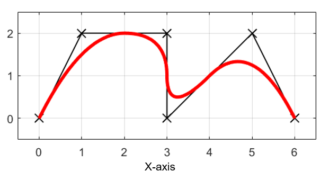
今回の記事では、これまでに紹介した知識を用いて実際に2次のBスプライン曲線を作成して離散点をスムーズに補間していきたいを思います。
取り扱う指令点
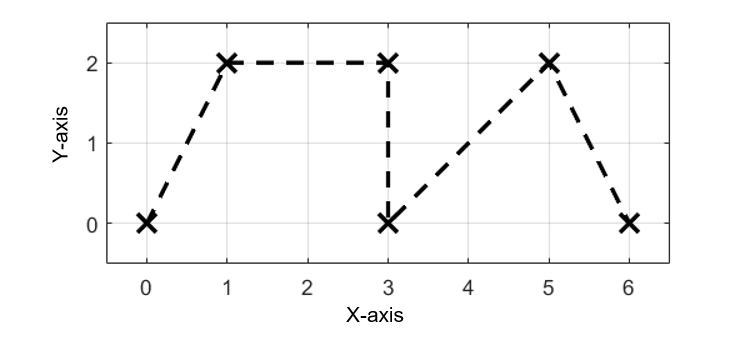
今回の記事では、上図のような離散的な指令点(✕)を2次のBスプライン曲線を用いて滑らかに補間します。
Bスプライン曲線の基本式
前回までの記事のおさらいです。
Bスプライン曲線の基本式は
$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(u) \ , \quad u \in [u_0,u_{m-1}] $$
と表されます。
また、B‐スプライン基底関数は
$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 \\ b_{j,k}(u) = \frac{u-u_j}{u_{j+k}-u_j} b_{j,k-1}(u) + \frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(u) \ , \quad j=0,1,\cdots, m-k-2 \end{array} \end{eqnarray} $$
のようにノットベクトルu内のノットを用いて定義されます。
今回は、これらの式を用いて与えられた指令点から具体的にB‐スプライン曲線を描く方法を紹介します。
ノットベクトルuの作成
今回の記事で与えられた指令点の数pは6です。
また、用いるBスプライン曲線の次数nは2とします。
よって、作成するノットベクトルu内のノット(要素)の数mは
$$ m = p + n + 1 $$
の関係式より、m=6+2+1=9と分かります。
よって、ノット数m=9の開一様ノットベクトルuを求めていきます。
開一様ノットベクトルuについての詳細は、こちらの記事を参考にしてください。

Bスプライン曲線の次数n=2より、ノットベクトルuの始めと終わりのn+1=3個のノットは同じ値になるため
$$ \boldsymbol{u} = [0,0,0,\cdot,\cdot,\cdot,1,1,1] $$
となります。
そして、残った9-3×2=3個のノットを均等に配置すると
$$ \boldsymbol{u} = [0,0,0,0.25,0.5,0.75,1,1,1] $$
のように、ノットベクトルuを作成することが出来ました。
Bスプライン基底関数を求める
Bスプライン基底関数の式を基に実際にBスプライン基底関数の様子を求めていきます。
Bスプライン基底関数についての詳しい説明は、こちらの記事を参考にしてください。
まずBスプライン基底関数bj,0
$$ b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, 7 $$
について、先ほど求めたノットベクトルu
$$ \boldsymbol{u} = [0,0,0,0.25,0.5,0.75,1,1,1] $$
を用いて算出した結果は下図のようになります。
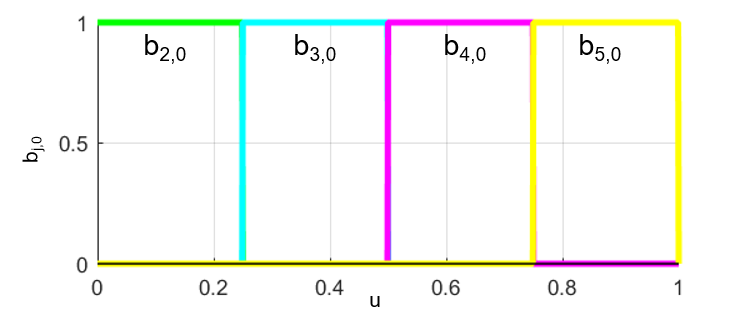
図から分かるように、j=2から5までのb2,0からb5,0はそれぞれの範囲(ujからuj+1)で1となっています。
また、j=0,1,6,7の場合についてbj,0は常に0という結果になりました。
次に、求めたbj,0を用いてbj,1
$$ b_{j,1}(u) = \frac{u-u_j}{u_{j+1}-u_j} b_{j,0}(u) + \frac{u_{j+2}-u}{u_{j+2}-u_{j+1}} b_{j+1,0}(u) \ , \quad j=0,1,\cdots, 6 $$
を求めた結果が下図のようになります。

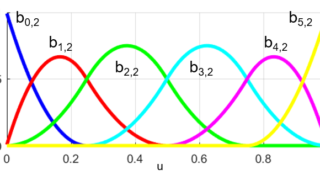
さらにbj,2
$$ b_{j,2}(u) = \frac{u-u_j}{u_{j+2}-u_j} b_{j,1}(u) + \frac{u_{j+3}-u}{u_{j+3}-u_{j+1}} b_{j+1,1}(u) \ , \quad j=0,1,\cdots, 5 $$
は下図のように求めることが出来ました。
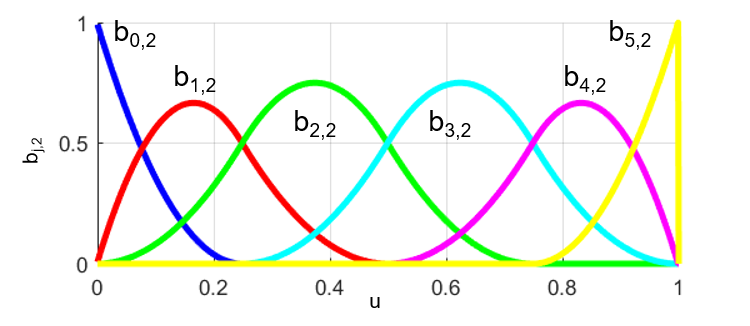
この算出したbj,2を用いて、与えられたp個の指令点Piを滑らかなBスプライン曲線で補間していきます。
Bスプライン曲線での補間結果
与えられたp個の指令点Piを2次のBスプライン曲線を用いて補間した結果は下図のようになります。
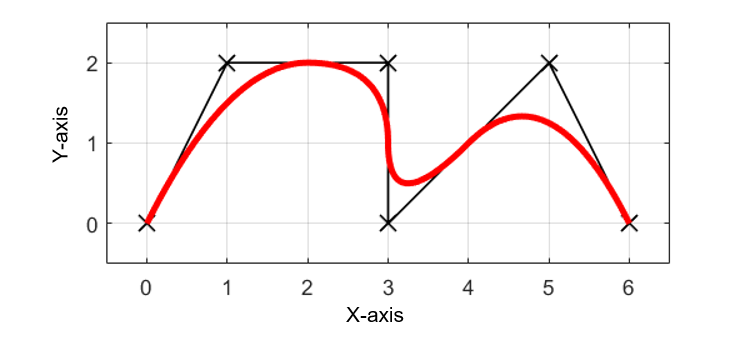
離散的で不連続であった指令点(黒✕)がBスプライン曲線を用いて滑らかな曲線(赤線)で補間されていることが分かります。
これより、ロボットや工作機械に与えられた目標位置(指令値)が不連続で離散的であった場合でも、Bスプライン曲線を用いて連続的で滑らかな曲線に変換することで、スムーズに制御することが可能になります。
まとめ
今回は、実際に2次のBスプライン曲線を用いて、与えられた離散的な指令点を滑らかにBスプライン補間する方法を紹介しました。
紹介したB‐スプライン曲線を用いることで、ロボットの目標位置が飛び飛びで与えられた場合でも、問題なく間をスムーズな曲線で補間することが出来ます。
今回用いたプログラムを紹介した記事はこちらです。


























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+

質問です,直線からスプライン曲線を作ることは可能でしょうか?
ご質問ありがとうございます。
与えられた指令点が直線上にある場合に、Bスプライン曲線で補間可能かという質問でしょうか。
そうでしたら、直線からBスプライン曲線を作ることは可能です。
参考になりましたら幸いです。