Bスプライン曲線を使ってロボットの軌跡生成をしてみよう！（その２）

前回の記事から、Bスプライン曲線を用いた離散的で不連続な指令点を連続で滑らかに補間する方法を紹介しています。

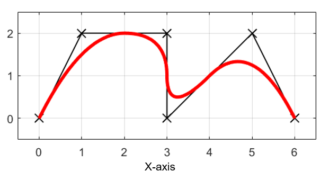
Bスプライン曲線を使ってロボットの軌跡生成をしてみよう！（その１）前回の記事では、Bスプライン曲線とベジエ曲線について、それぞれの特徴と関係性を説明し、ロボットの軌跡生成への応用例を紹介しました...

今回の記事では、Bスプライン曲線の基本式に含まれているBスプライン基底関数の作成方法とを紹介していきます。

Contents

Bスプライン曲線の基本式
Bスプライン基底関数
- b_j,0(u)の式について
- b_j,k(u)の式について
まとめ

Bスプライン曲線の基本式

前回のおさらいです。

Bスプライン曲線の基本式は

$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(u) \ , \quad u \in [u_0,u_{m-1}] $$

と表されます。

基本式からも分かるように、Bスプライン曲線は、制御点（Control Point、P_i）とノットベクトル（Knot Vector、u）を用いて定義されるBスプライン基底関数（B-spline Basis Function、b_i,n）で求めることが出来ます。

今回は、前回の記事で紹介したノットベクトルuを用いて、Bスプライン基底関数b_i,nを作成する方法を紹介します。

ノットベクトルの詳しい作り方は、こちらの記事を参考にしてください。

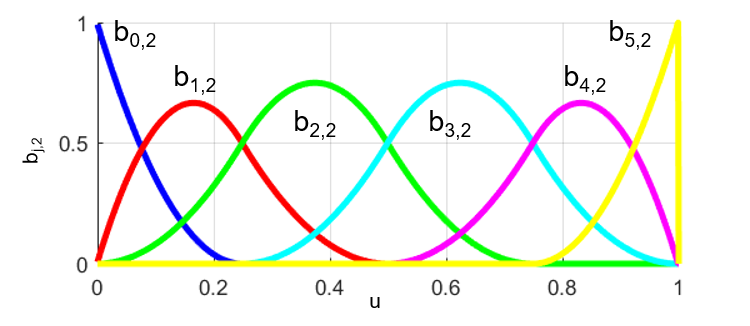
Bスプライン基底関数

作成したノットベクトルuを用いて、Bスプライン基底関数を作成します。

B‐スプライン基底関数は

$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 \\ b_{j,k}(u) = \frac{u-u_j}{u_{j+k}-u_j} b_{j,k-1}(u) + \frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(u) \ , \quad j=0,1,\cdots, m-k-2 \end{array} \end{eqnarray} $$

のようにノットベクトルu内のノットを用いて定義されます。

ここで、b_i,nはBスプライン基底関数、u_jはノットベクトルu内にしてください。含まれるm個のノットの内j番目のノットです。

b_j,0(u)の式について

まず、１つ目のb_j,0(u)の式について説明していきます。

$$ b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 $$

この式は、変数uが指定された範囲内なら1を、それ以外なら0を返すということを表しています。

例えば簡単な例としてノットベクトルuが

$$ \boldsymbol{u} = [0,1,2,3,4] $$

の一様ノットベクトルの場合を考えます。

この場合、b_0,0の値は変数uがu₀からu₁の間なら1をそれ以外なら0となるため、変数uが0から1の間は1となり、それ以外の範囲である1から4の間は0になります。

同様に、b_1,0の値は変数uがu₁からu₂の間なら1をそれ以外なら0となるため、変数uが1から2の間は1となり、それ以外の範囲である0から1の間と2から4の間は0になります。

今回のシリーズで用いる開一様ノットベクトルの場合も同様な考え方でb_j,0(u)を求めることが出来ます。

開一様ノットベクトルの例としてノットベクトルuが

$$ \boldsymbol{u} = [0,0,0,0.25,0.5,0.75,1,1,1] $$

と与えられた場合を考えます。

この時のb_0,0の値は変数uがu₀からu₁の間なら1をそれ以外なら0となりますが、u₀とu₁が同じ値（0）であり1となる範囲が存在しないため、常に0を返すことになります。

またb_1,0も同様に常に0を返します。