以前の記事では、移動ロボットや工作機械などに与えられた離散的な指令点を、2次のBスプライン曲線(またはB-スプライン曲線)を用いて補間する方法(B-spline Interpolation)を紹介しました。
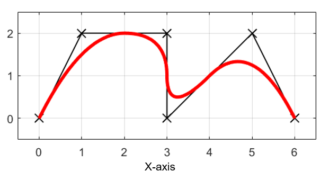
今回は、取り扱うBスプライン曲線の次数を3次、4次、5次と上げた場合について、出来上がる曲線の様子を確認してみたいと思います。
取り扱う問題とBスプライン曲線
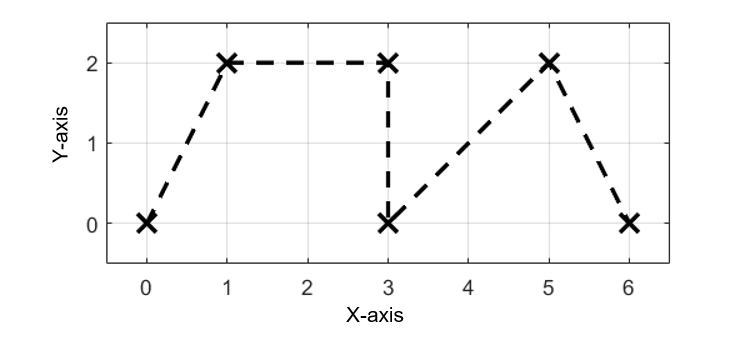
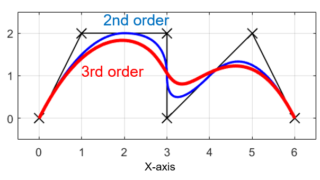
今回の記事では、図のような離散的な6点の指令点(✕)が与えられた場合について、Bスプライン曲線を用いて滑らかに補間します。
Bスプライン曲線の基本式は
$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ p-1 } \boldsymbol{ P }_i b_{i,n}(u) \ , \quad u \in [u_0,u_{m-1}] $$
と表されます。
また、B‐スプライン基底関数は
$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, m-2 \\ b_{j,k}(u) = \frac{u-u_j}{u_{j+k}-u_j} b_{j,k-1}(u) + \frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(u) \ , \quad j=0,1,\cdots, m-k-2 \end{array} \end{eqnarray} $$
のようにノットベクトルu内のノットを用いて定義されます。
ここで、求めるBスプライン曲線の次数nを3とすると、今回の記事で与えられた指令点の数pは6なので、ノットベクトルu内のノット数mは
$$ m = p + n + 1 = 6 + 3 + 1 = 10 $$
より、このBスプライン曲線の基本式は
$$ \boldsymbol{ S }(u) = \displaystyle \sum_{ i = 0 }^{ 5 } \boldsymbol{ P }_i b_{i,3}(u) \ , \quad u \in [u_0,u_9] $$
となります。
同様に、Bスプライン基底関数も
$$ \begin{eqnarray} \begin{array}{l} b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, 8 \\ b_{j,k}(u) = \frac{u-u_j}{u_{j+k}-u_j} b_{j,k-1}(u) + \frac{u_{j+k+1}-u}{u_{j+k+1}-u_{j+1}} b_{j+1,k-1}(u) \ , \quad j=0,1,\cdots, 8-k \end{array} \end{eqnarray} $$
のように書き換えることが出来ます。
今回は、ノットベクトルuとして開一様ノットベクトルを用います。
与えられたp=6点の指令点を次数n=3のBスプライン曲線で保管する場合の開一様ノットベクトルuは
$$ \boldsymbol{u} = [0,0,0,0,0.333,0.667,1,1,1,1] $$
となります。
2次Bスプライン曲線と3次Bスプライン曲線
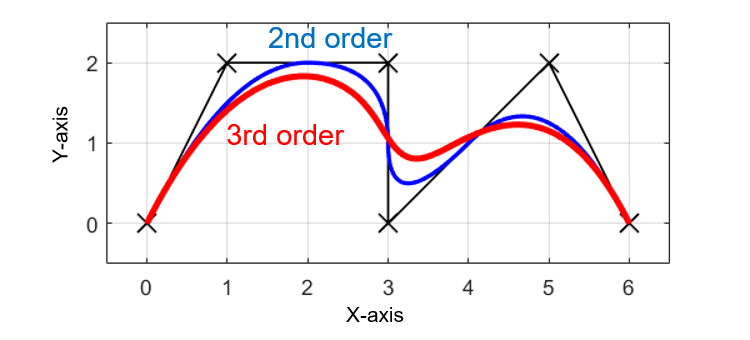
上の図は、実際に3次のBスプライン曲線を使用して離散点を補間した結果を2次のBスプライン曲線の場合と比較した結果です。
3次Bスプライン補間(赤線)の方が2次Bスプライン補間(青線)よりもカーブが緩くスムーズな曲線となっていることが分かります。
また、3次Bスプライン補間の方が2次Bスプライン補間よりも与えられた元の軌跡(黒✕線)との差が大きいことも分かります。
Bスプライン基底関数
実際に3次のBスプライン曲線を描くために用いたB-スプライン基底関数の様子を紹介します。
まず、Bスプライン基底関数bj,0は下図のようになります。
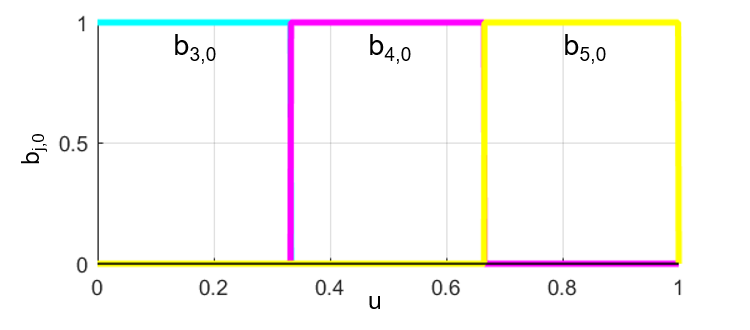
この時のBスプライン基底関数bj,0についての式は
$$ b_{j,0}(u) := \left\{ \begin{array}{l} 1 \quad \mathrm{if} \ u_j \leq u \lt u_{j+1}\\ 0 \quad \mathrm{otherwise} \end{array} \right. \ , \quad j=0,1,\cdots, 8 $$
と表されます。
同様に、Bスプライン基底関数bj,1は下の図のように表されます。
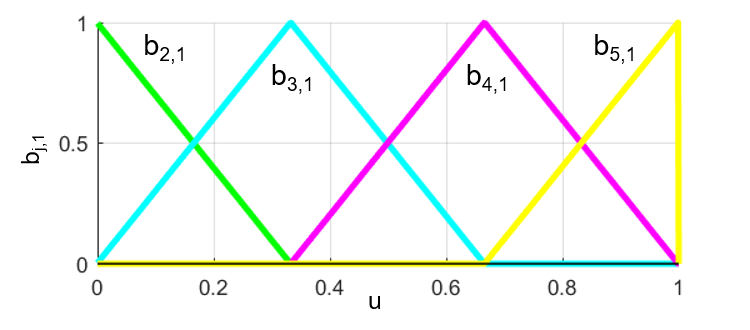
さらに、Bスプライン基底関数bj,2は下図のようにスムーズになっていきます。
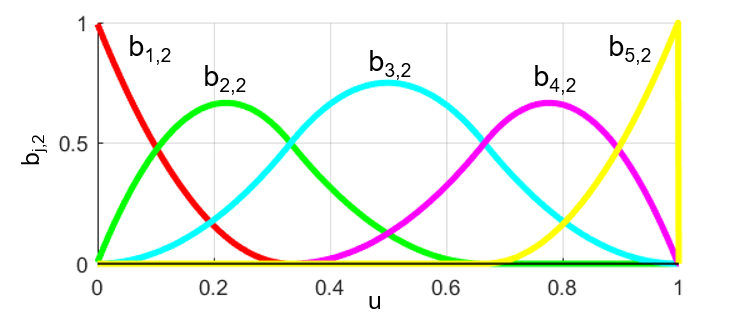
そして、実際に3次のBスプライン曲線を描くために使用するBスプライン基底関数bj,3は下図のように求めることが出来ました。
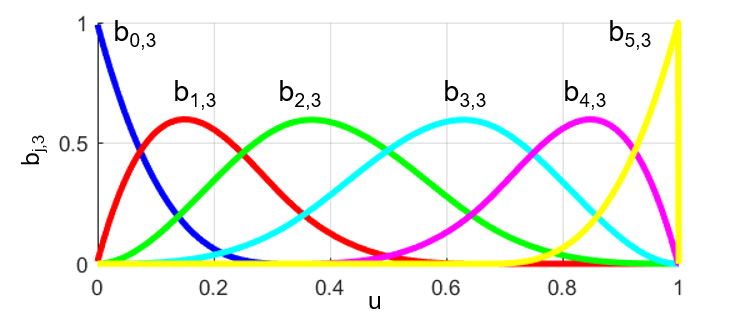
この時のBスプライン基底関数bj,3は
$$ b_{j,3}(u) = \frac{u-u_j}{u_{j+3}-u_j} b_{j,2}(u) + \frac{u_{j+4}-u}{u_{j+4}-u_{j+1}} b_{j+1,2}(u) \ , \quad j=0,1,\cdots, 5 $$
のような式で表されます。
Bスプライン基底関数の比較
ちなみに、前回の記事で紹介した2次のBスプライン曲線を用いた場合のBスプライン基底関数bj,2は下の図のような関数でした。
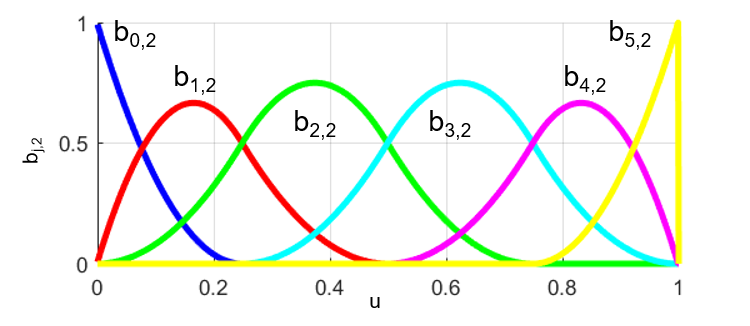
3次の場合と2次の場合のBスプライン基底関数を比較すると、3次B-スプライン曲線の場合の方がB-スプライン基底関数がより滑らかになっていることが分かります。
Bスプライン曲線の比較
先ほど求めたBスプライン基底関数を用いて3次のBスプライン曲線を描いていきます。
今回は、前回紹介した2次のBスプライン曲線に加えて、同様の手法で求めた4次と5次のBスプライン曲線も併せてグラフにしました。
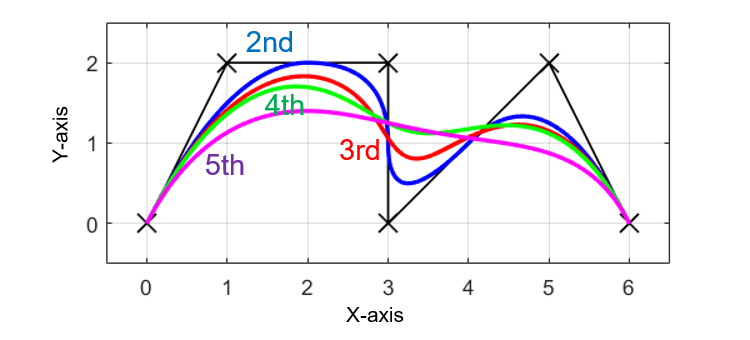
求めた結果より、B-スプライン曲線の次数が2次(青線)、3次(赤線)、4次(緑線)、5次(紫線)と上がるほど曲線がスムーズになっていることが分かります。
しかし、元の指令点(黒✕)との差については、Bスプライン曲線の次数が上がるほど大きくなっていることも分かります。
ちなみに、今回用いた指令点は6点なので、Bスプライン曲線の次数は5次が最大になり、6次のBスプライン曲線は適用できません。
まとめ
今回は、取り扱うBスプライン曲線の次数を変化させた場合の補間後の軌跡の様子を比較しました。
比較結果より、Bスプライン曲線の次数を上げていくことで、
- よりスムーズに指令点が補間されるが、
- 元の指令点による軌跡との差は大きくなる
という特徴になる事が分かりました。
必要となるスムーズさ、許容できる指令点との誤差を考慮して、最適なB-スプライン曲線の次数を選択することが、ロボットの軌跡生成では重要となります。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
