ロボットの軌跡生成：移動平均関数を使って加減速を制御する

ロボットが移動する際に加速度を考慮した軌跡生成の方法として、

• 指数関数型（Exponential Model）
• 移動平均型（Moving Average Model）

があります。

今回は移動平均関数（Moving Average Function）を用いた方法について、より詳しく紹介していきます。

指数関数を用いた加減速制御については、こちらの記事を参考にしてください。

ロボットの軌跡生成：指数関数を使って加減速を制御する ロボットが移動する際に加速度を考慮した軌跡生成の方法として、 指数関数型 移動平均型 の2つを前回の記事で...

移動平均型

移動平均型の加減速制御とは、移動平均関数を用いてロボットの速度をスムーズに変化させる方法です。

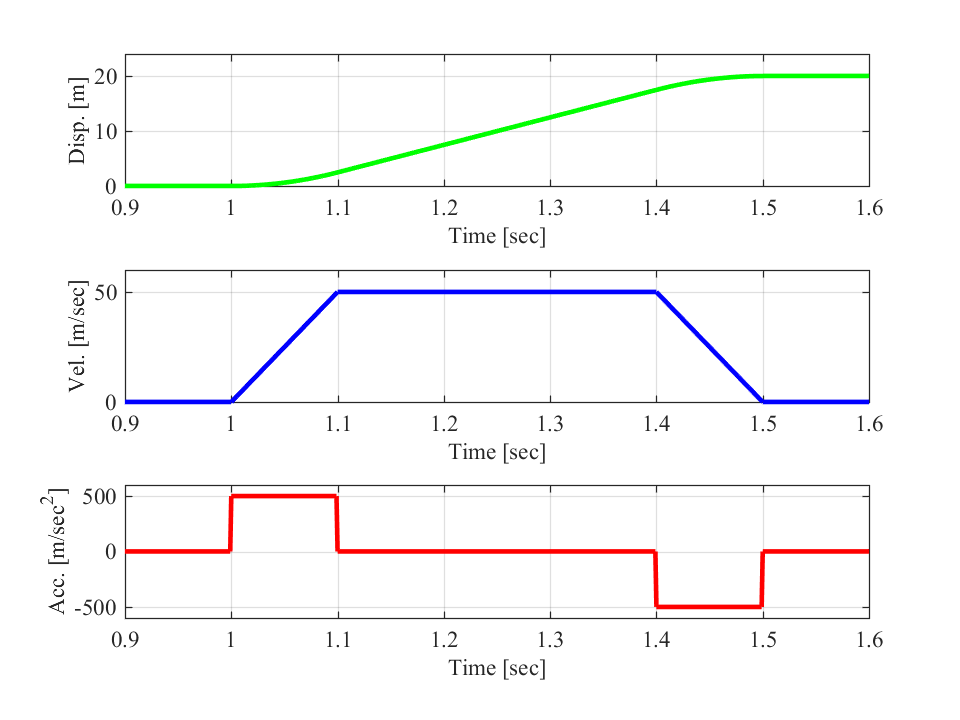
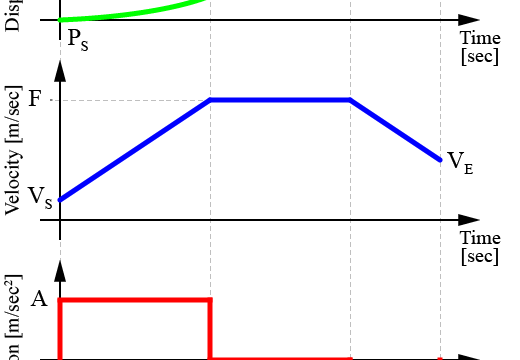
図のように、移動平均関数を用いた軌跡生成では、加減速時の加速度（下段）の値は一定という特徴があります。

そのため、ロボットの速度（中段）も一定の傾きで目標値まで変更されます。

移動平均型の加減速制御の利点としては、

• 加減速時の加速度の振幅を容易に制御できる、
• 目標の速度へ達する時間を短くできる

といった点がありますが、欠点として、

• 加速度波形が加減速開始および終了時に不連続となるため、ロボットが衝撃を受ける

といった点があります。

移動平均関数のラプラス変換

時間領域\(t\)の移動平均関数をラプラス変換を用いて周波数領域\(s\)にすると、

$$ G(s) = \frac{1-e^{- s T}}{s T} $$

という形で表すことが出来ます。

この\(T\)の値を変えることで、ロボットの加速度を制御します。

\(T\)を変化させた時の変化

移動平均関数内の\(T\)の値を変化させた時の軌跡生成に与える影響を調査するため

$$ T = 0.05, 0.1, 0.2 $$

の3パターンの\(T\)を持いて移動平均関数を設計し、軌跡生成を行います。

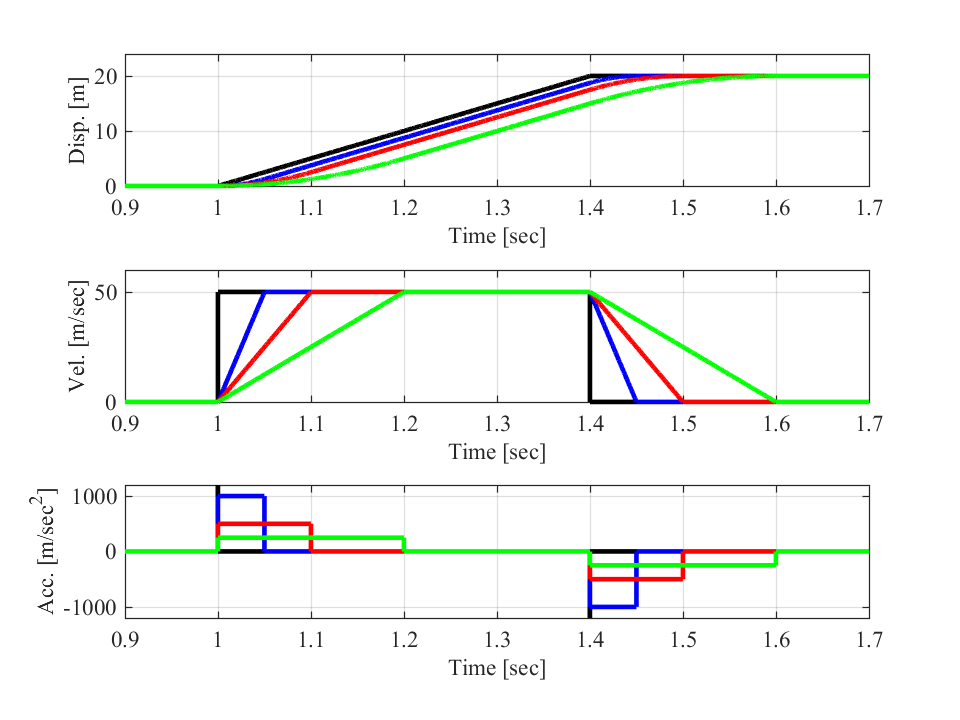
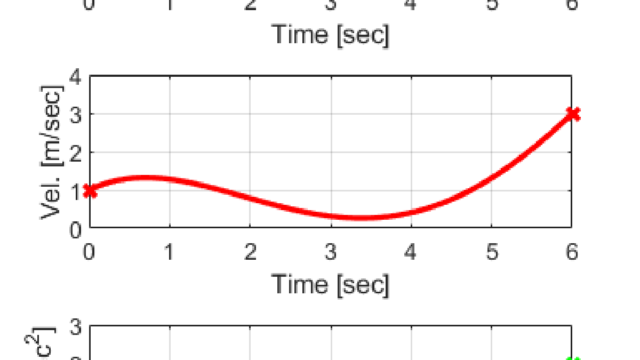
グラフについて、\(T=0.05\)が青線、\(T=0.1\)が赤線、\(T=0.2\)が緑線となります。

黒線は指数関数を用いない場合の波形です。

生成した軌跡の速度波形（中段）を見ると、\(T\)の値が小さいほど速度が立ち上がる傾きが大きくなり、目標の速度に達する時間が短くなります。

反対に\(T\)の値が大きくなると速度が立ち上がる傾きが緩やかになり、目標速度に到達する時間も長くなることが分かります。

次に加速度波形（下段）を見ると、\(T\)の値が小さいほど加減速時の加速度波形の振幅が大きくなり、\(T\)の値が大きくなるにつれて振幅は小さくなることが分かります。

この時の加速度波形のピークの値（最大加速度）は、

$$ A = \frac{F}{T} $$

で求めることが出来ます。

これより、\(T\)の値を調整することで、モータの最大出力や速度の立ち上がりにかかる目標時間に合わせて軌跡を調整することが出来ます。

まとめ

今回は加速度を制限の方法として移動平均を用いた軌跡生成の方法を紹介しました。