軌跡を生成するための基本的な関数の紹介

ロボットや工作機械を指令値通りに滑らかに制御する際、滑らかな軌跡の生成は重要な要素の1つになります。

滑らかな軌跡を生成する方法として、様々な関数が用いられています。

今回の記事では、軌跡生成に用いられる基本的な関数を紹介します。

軌跡生成に用いられる関数の種類

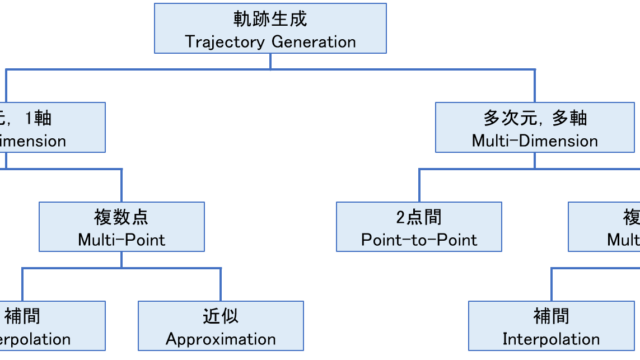
軌跡生成の手法は、主に4種類に大別することが出来ます。

まず、軌跡生成に用いられる基本的な関数として、

• 多項式関数（Polynomial Function）
• 三角関数（Trigonometric Function）
• 指数関数（Exponential Function）

の3種類の関数があります。

この3種類の関数に加えて、

• フーリエ級数展開（Fourier Series Expansion）

を用いた軌跡生成手法があります。

今回はこの4種類について、簡単に説明したいと思います。

多項式関数による軌跡生成

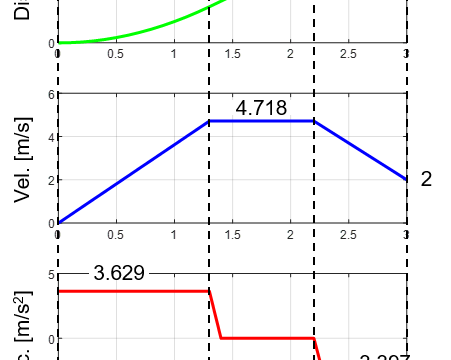
多項式関数を軌跡生成に用いることで、軌跡の開始点と終了点での制約条件を満足する軌跡を実現することが出来ます。

多くの場合において、軌跡の開始点と終了点では、位置や速度、加速度といった条件が与えられます。

軌跡を生成する際には、この与えられた制約条件を満足する必要があります。

軌跡の生成に多項式関数を用いることで、これら終端での制約条件を満足した滑らかな軌跡が生成できます。

三角関数による軌跡生成

三角関数を軌跡生成に用いることで、位置指令の微分を繰り返した波形にも連続性を持たせることが出来ます。

位置のみでなく、速度や加速度、躍度が連続であると、より滑らかにロボットや工作機械を動作させることが出来ます。

三角関数は連続的な性質を持ちます。

そして、この三角関数の微分も、また三角関数で表されることから連続性を保ちます。

三角関数を位置指令の生成に用いることで、その速度や加速度、躍度指令も連続な軌跡となります。

指数関数による軌跡生成

指数関数を軌跡生成に用いることで、システムの固有振動に起因する振動を低減することが出来ます。

生成された軌跡の速度や加速度に不連続な部分があると、ロボットや機械に振動が生じます。

そのため、軌跡は使用用途に合わせて十分に滑らかである必要があります。

速度指令の生成に指数関数を用いることで、滑らかで連続した軌跡が生成できます。

フーリエ級数展開を用いた軌跡生成

フーリエ級数展開を軌跡生成に用いることで、加速度波形に含まれる特定の周波数成分を除去することが出来ます。

加速度の最大値を抑えることで、機体に発生する振動を低減させることが出来ます。

しかし、加速度の最大値を抑えたとしても、加速度指令が不連続であると機体に振動が発生してしまいます。

フーリエ級数展開を用いて軌跡を周波数領域で取り扱うことで、特定の周波数成分のみ取り除くことが可能となり、軌跡は残された周波数成分により連続で滑らかになります。

まとめ

今回の記事では、軌跡生成に用いられる基本的な関数について、それぞれの特徴を紹介しました。

これらの関数を用途に合わせて使い分けることで、望み通りにロボットや機械を制御することが可能になります。