4つの制御点を通る3次スプライン曲線の描き方

4つの離散点（制御点）を通る滑らかな曲線を、3次スプライン曲線による近似を用いて生成する方法を紹介します。

今回の記事では、位置の制約条件のみを取り扱います。

つまり、速度や加速度の制約条件は与えられていない場合を考えます。

ちなみに、この位置の制約条件により得られた3次スプライン曲線を用いることで、5次スプライン補間を行う際に必要となる補間条件（制約条件）を求めることが出来ます。

3次スプライン曲線とは

今回の記事で紹介する3次スプライン曲線は、4つの制御点を通る3次のスプライン曲線のことを言います。

3次スプライン曲線の基本式

この3次スプライン曲線の式は

$$ S_i (u) = a_i u^3 + b_i u^2 + c_i u + d_i $$

で表されます。

ここで、3次スプライン曲線の変数uは

$$ u \in \begin{bmatrix} 0, \displaystyle \sum_{ i }^{ i+2 } l_i \end{bmatrix}, \ \ l_i = \vert \boldsymbol{ P_{i+1} } – \boldsymbol{ P_i } \vert $$

のように、与えられた制御点間の距離を用いて表されます。

3次スプライン曲線と制御点

今回の記事では、与えられた4つの制御点を通る3次のスプライン曲線を描く方法を取り扱っています。

つまり、下の図のように3次スプライン曲線を4つの制御点にフィッティングさせて曲線近似する方法を考えます。

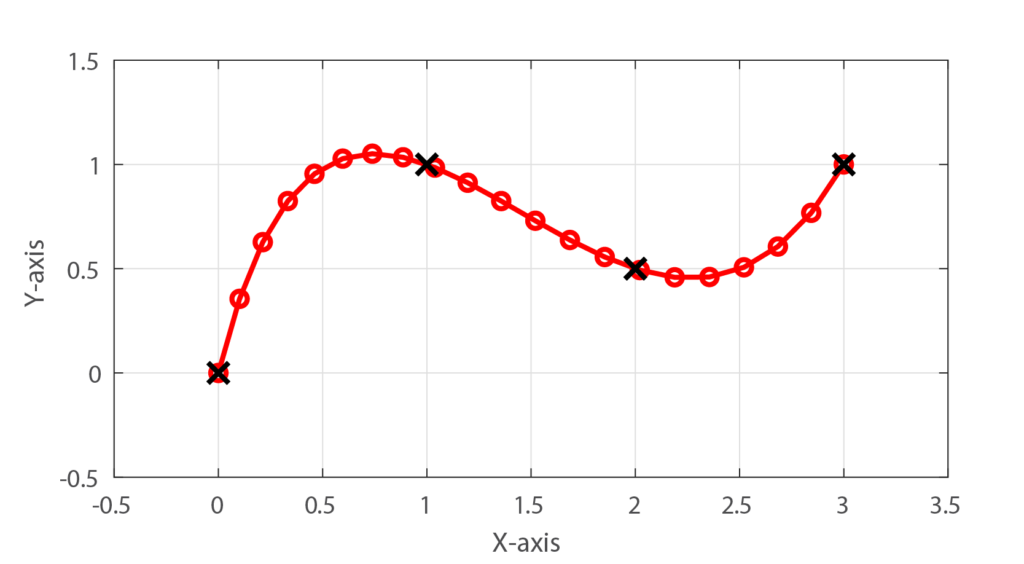
このように離散的な制御点（黒✕）が与えられた場合に、これらの離散点を通る3次のスプライン曲線（赤線）を考えます。

3次スプライン補間の制約条件

今回の記事で取り扱う、4つの制御点（離散点）を通る3次スプライン曲線を描くための制約条件は、各制御点での位置です。

3次スプライン曲線の各位置での制約条件を表すと下の式のようになります。

$$ \begin{eqnarray} \left\{ \begin{array}{l} S_i (u_0) = S_i (0) = P_i \\ S_i (u_1) = S_i (l_i) = P_{i+1} \\ S_i (u_2) = S_i (l_i+l_{i+1}) = P_{i+2} \\ S_i (u_3) = S_i (l_i+l_{i+1}+l_{i+2}) = P_{i+3} \end{array} \right. \end{eqnarray} $$

3次スプライン曲線の基本式に含まれる4つのパラメータ（a、b、c、d）を求めるために、4つの制御点の位置を制約条件として用います。

つまり、各制御点における速度や加速度といった値は、制約条件として用いません。

3次スプライン補間との違い

今回の記事では、3次スプライン曲線を用いた4つの離散点（制御点）を補間する方法として、3次スプライン曲線を用いた離散点を通る曲線近似の手法を紹介しています。

またもう一つの3次スプラインを用いた軌跡生成の手法として、以前の記事では3次スプラインにより離散点を補間する方法を紹介しました。

3次スプライン補間で軌跡生成：３次多項式と補間条件 ロボットなどを動かす経路を指定する際に、通過してほしい点を離散的な指令点で指示することが多くあります。 この様な離...

この2つの手法は取り扱う人により定義がバラバラなので、私なりの使い分けを紹介したいと思います。

• 3次スプラインを用いた離散点の補間
• 3次スプラインを用いた離散点を通る曲線近似

3次スプラインを用いた離散点の補間

以前の記事で紹介した3次スプライン曲線を用いた離散点補間では、それぞれの離散点間を3次のスプラインで補間します。

この時の3次スプライン曲線のパラメータは、各離散点間で異なります。

そのため、離散点間毎にパラメータを算出して、異なる特性の3次スプライン曲線を用いて滑らかな軌跡を生成します。

しかし各離散点ごとにスプライン曲線を取り扱うため、制御点（離散点）が増えた場合も対応することが出来ます。

3次スプラインを用いた離散点を通る曲線近似

今回の記事で紹介している3次スプライン曲線による離散点の曲線近似では、4つの離散点を3次のスプライン曲線で結ぶことで補間します。

この時の3次スプライン曲線のパラメータは、4つの離散点を通る曲線すべてで同じ値を用います。

そのため、1つの3次スプライン曲線で4つの離散点のすべてを通る滑らかな軌跡を生成することが出来ます。

ただ新しく制御点（離散点）が増えた場合は、そのままでは対応することが出来ず、スプラインの次数を増やすなどの対応をする必要があります。

まとめ

今回の記事では、3次スプライン曲線を用いた離散的な制御点を通る滑らかな軌跡を生成する方法を紹介しました。

今回紹介した3次スプラインによる曲線近似を用いることで、与えられた離散点から滑らかな軌跡を生成することが可能になります。

次回の記事では、実際に具体的な値を使った例を用いながら3次スプラインによる離散的な制御点の曲線近似の方法を紹介したいと思います。

実際に3次スプライン曲線で離散的な指令点を補間してみよう！ スプライン曲線を用いることで、離散点を滑らかに補間することが可能になります。 今回の記事では、3次スプラインを使っ...

合わせて読みたい

N次スプラインによる曲線近似について紹介しています。

N次スプライン曲線でN+1個の離散点を滑らかに補間する方法 N次のスプラインを用いることで、N+1個の離散的な点を通る滑らかな軌跡を、曲線近似により生成することが出来ます。 ...