スプライン曲線を用いることで、離散点を滑らかに補間することが可能になります。
今回の記事では、3次スプラインを使った4つの離散的な指令点を通る曲線を生成する方法を紹介します。
3次スプラインによる曲線近似の基本
与えられた離散点について、スプライン曲線による曲線近似を行うことで、滑らかな軌跡を生成することが出来ます。
ここでは、3次スプライン曲線の基本式と、式に含まれるパラメータを算出するための制約条件について紹介します。
3次スプライン曲線の基本式
4個の離散的な制御点(指令点)Piを曲線近似するための3次のスプライン曲線の基本式は
$$ S_i (u) = a_i u^3 + b_i u^2 + c_i u + d_i $$
と表されます。
この3次スプライン曲線の基本式に含まれる変数uは
$$ u \in \begin{bmatrix} 0, \displaystyle \sum_{ i }^{ i+2 } l_i \end{bmatrix}, \ \ l_i = \vert \boldsymbol{ P_{i+1} } – \boldsymbol{ P_i } \vert $$
のように、与えられた制御点Pi間の距離を用いて表されます。
3次スプライン曲線の制約条件
そして、この基本式に含まれる各パラメータを算出するための制約条件は、制御点Piの位置情報から
$$ \begin{eqnarray} \left\{ \begin{array}{l} S_i (u_0) = S_i (0) = P_i \\ S_i (u_1) = S_i (l_i) = P_{i+1} \\ S_i (u_2) = S_i (l_i+l_{i+1}) = P_{i+2} \\ S_i (u_3) = S_i (l_i+l_{i+1}+l_{i+2}) = P_{i+3} \end{array} \right. \end{eqnarray} $$
と与えることが出来ます。
この制約条件からスプライン曲線の基本式に含まれるをパラメータを導くとこで、与えられた離散的な制御点を滑らかに結ぶスプライン曲線を得ることが出来ます。
3次スプラインによる曲線近似の詳細は、こちらの記事を参考にしてください。
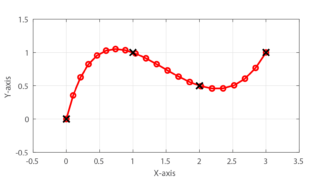
離散点の曲線近似
ここでは、実際に具体的な値を用いながら3次スプラインによる曲線近似の流れを紹介します。
シミュレーション条件
今回のシミュレーションでは、補間したい離散的な4つの制御点Piを
$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{ P_0 } = \begin{bmatrix} 0 & 0 \end{bmatrix}^T \\ \boldsymbol{ P_1 } = \begin{bmatrix} 1 & 1 \end{bmatrix}^T \\ \boldsymbol{ P_2 } = \begin{bmatrix} 2.5 & 0.5 \end{bmatrix}^T \\ \boldsymbol{ P_3 } = \begin{bmatrix} 4 & 1 \end{bmatrix}^T \end{array} \right. \end{eqnarray} $$
と定義します。
そして、この離散点P0からP3の4点を通る滑らかな3次スプライン曲線を求めていきます。
制約条件の算出
3次スプライン曲線に含まれるパラメータを算出するために、制約条件を求める必要があります。
この制約条件は、曲線補間したい離散点Piの位置から導くことが出来ます。
まず、離散点Pi間の距離から各離散点を通過する際の変数uiの値を
$$ u_i = u_{i-1} + \sqrt{(P_{i,x}-P_{i-1,x})^2+(P_{i,y}-P_{i-1,y})^2} $$
の式から求めます。
これより、各離散点を通過する際の変数uiの値は
$$ \begin{eqnarray} \left\{ \begin{array}{l} u_0 = 0 \\ u_1 = 0 + \sqrt{(1-0)^2+(1-0)^2} = 1.4142 \\ u_2 = 1.4142 + \sqrt{(2.5-1)^2+(0.5-1)^2} = 2.9954 \\ u_3 = 2.9954 + \sqrt{(4-2.5)^2+(1-0.5)^2} = 4.5765 \end{array} \right. \end{eqnarray} $$
と求めることが出来ました。
算出した変数の値uiと与えられた制御点Piの位置の情報から、今回の制約条件は
$$ \boldsymbol{S_i} (u_i) = \boldsymbol{ P_i } $$
の関係式より、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{S_i} (0) &=& \begin{bmatrix} 0 & 0 \end{bmatrix}^T \\ \boldsymbol{S_i} (1.4142 ) &=& \begin{bmatrix} 1 & 1 \end{bmatrix}^T \\ \boldsymbol{S_i} (2.9954 ) &=& \begin{bmatrix} 2.5 & 0.5 \end{bmatrix}^T\\ \boldsymbol{S_i} (4.5765 ) &=& \begin{bmatrix} 4 & 1 \end{bmatrix}^T \end{array} \right. \end{eqnarray} $$
と算出することが出来ました。
パラメータの算出
求めたいパラメータと制約条件との関係式は
$$ \begin{bmatrix} {u_0}^3 & {u_0}^2 & {u_0} & 1 \\ {u_1}^3 & {u_1}^2 & {u_1} & 1 \\ {u_2}^3 & {u_2}^2 & {u_2} & 1 \\ {u_3}^3 & {u_3}^2 & {u_3} & 1 \end{bmatrix} \begin{bmatrix} a_i \\ b_i \\ c_i \\ d_i \end{bmatrix} = \begin{bmatrix} P_i \\ P_{i+1} \\ P_{i+2} \\ P_{i+3} \end{bmatrix} $$
のように表すことが出来ます。
この関係式を解くことでスプライン曲線の基本式に含まれるパラメータを
$$ \begin{bmatrix} a_i \\ b_i \\ c_i \\ d_i \end{bmatrix} = \begin{bmatrix} {u_0}^3 & {u_0}^2 & {u_0} & 1 \\ {u_1}^3 & {u_1}^2 & {u_1} & 1 \\ {u_2}^3 & {u_2}^2 & {u_2} & 1 \\ {u_3}^3 & {u_3}^2 & {u_3} & 1 \end{bmatrix}^{-1} \begin{bmatrix} P_i \\ P_{i+1} \\ P_{i+2} \\ P_{i+3} \end{bmatrix} $$
と求めることが出来ます。
上記の式は1次元の場合ですが、2次元以上の場合でも同様に求めることが出来ます。
今回のシミュレーション条件のように2次元以上に変更すると
$$ \begin{bmatrix} {u_0}^3 & {u_0}^2 & {u_0} & 1 \\ {u_1}^3 & {u_1}^2 & {u_1} & 1 \\ {u_2}^3 & {u_2}^2 & {u_2} & 1 \\ {u_3}^3 & {u_3}^2 & {u_3} & 1 \end{bmatrix} \begin{bmatrix} {\boldsymbol{A_i}}^T \\ {\boldsymbol{B_i}}^T \\ {\boldsymbol{C_i}}^T \\ {\boldsymbol{D_i}}^T \end{bmatrix} = \begin{bmatrix} {\boldsymbol{P_i}}^T \\ {\boldsymbol{P_{i+1}}}^T \\ {\boldsymbol{P_{i+2}}}^T \\ {\boldsymbol{P_{i+3}}}^T \end{bmatrix} $$
となり、各軸におけるスプライン曲線のパラメータは
$$ \begin{bmatrix} {\boldsymbol{A_i}}^T \\ {\boldsymbol{B_i}}^T \\ {\boldsymbol{C_i}}^T \\ {\boldsymbol{D_i}}^T \end{bmatrix} = \begin{bmatrix} {u_0}^3 & {u_0}^2 & {u_0} & 1 \\ {u_1}^3 & {u_1}^2 & {u_1} & 1 \\ {u_2}^3 & {u_2}^2 & {u_2} & 1 \\ {u_3}^3 & {u_3}^2 & {u_3} & 1 \end{bmatrix}^{-1} \begin{bmatrix} {\boldsymbol{P_i}}^T \\ {\boldsymbol{P_{i+1}}}^T \\ {\boldsymbol{P_{i+2}}}^T \\ {\boldsymbol{P_{i+3}}}^T \end{bmatrix} $$
と求めることが出来ます。
よって、今回の制約条件での3次スプライン曲線のパラメータは
$$ \begin{eqnarray} \begin{bmatrix} {\boldsymbol{A_i}}^T \\ {\boldsymbol{B_i}}^T \\ {\boldsymbol{C_i}}^T \\ {\boldsymbol{D_i}}^T \end{bmatrix} &=& \begin{bmatrix} 0^3 & 0^2 & 0 & 1 \\ 1.4142^3 & 1.4142^2 & 1.4142 & 1 \\ 2.9954^3 & 2.9954^2 & 2.9954 & 1 \\ 4.5765^3 & 4.5765^2 & 4.5765 & 1 \end{bmatrix}^{-1} \begin{bmatrix} 0 & 0 \\ 1 & 1 \\ 2.5 & 0.5 \\ 4 & 1 \end{bmatrix} \\ &=& \begin{bmatrix} -0.0176 & 0.1184 \\ 0.1584 & -0.8635 \\ 0.5184 & 1.6916 \\ 0 & 0 \end{bmatrix} \end{eqnarray} $$
と求めることが出来ました。
シミュレーション結果
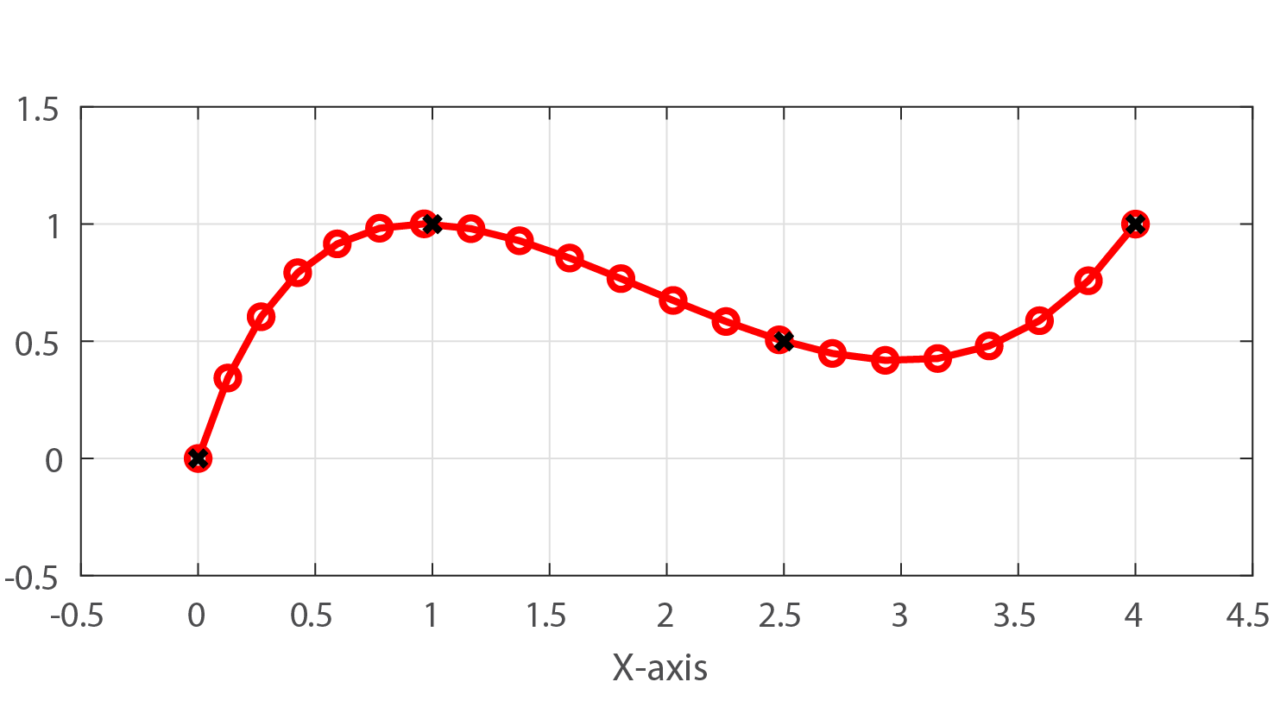
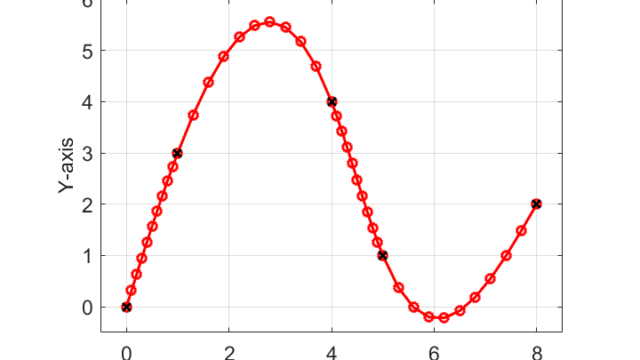
算出したパラメータを用いて3次スプライン曲線を書くと下の図のようになります。
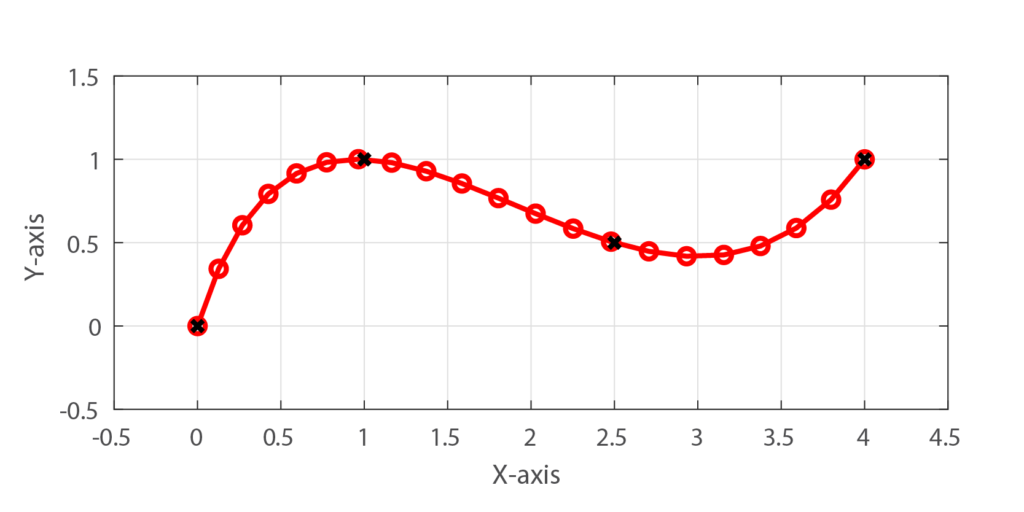
これより、求めた3次スプライン曲線(赤線)は与えられた4つの離散点(黒✕)を結ぶ滑らかな曲線をなっていることが分かります。
まとめ
今回は、実際に4つの離散的な制御点が与えられた場合に、3次スプライン曲線補間を行う流れを紹介しました。
紹介した方法を用いることで、ロボットを制御するために離散点が与えられた際に、それらを滑らかに結ぶ軌跡生成を行うことが出来ます。
合わせて読みたい
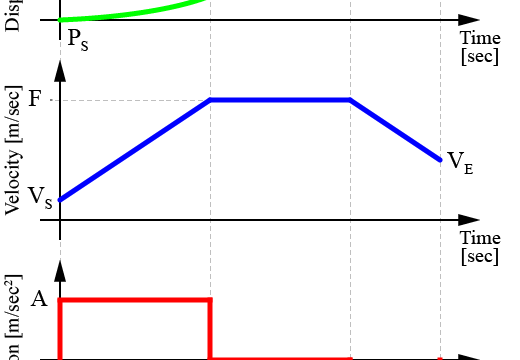
N次スプラインによる曲線近似について紹介しています。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
