入力ありの質量-ばね-ダンパーモデルの運動を求める

今回は、質量-ばね-ダンパーモデルを用いて、入力として力が質量に与えられている場合のシステムの運動を考えます。

入力がない場合は、こちらの記事を参考にしてください。

質量-ばね-ダンパーシステムの運動を求める今回は質量-ばね-ダンパーシステム（Damped Mass Spring System）を用いて、モデルの振動（運動）について考...

Contents

入力ありの質量-ばね-ダンパーシステム（Forced Mass Spring Damper System）
システムの運動方程式
定常解を求める
まとめ

入力ありの質量-ばね-ダンパーシステム（Forced Mass Spring Damper System）

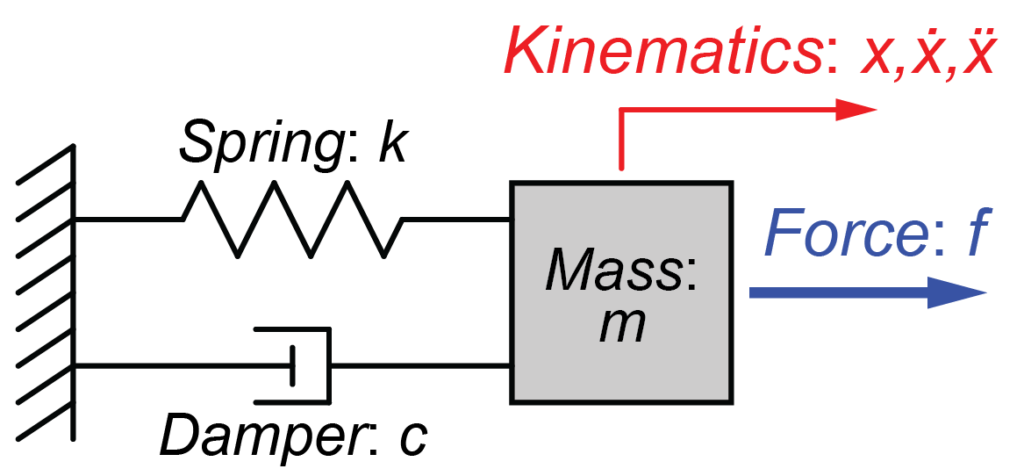
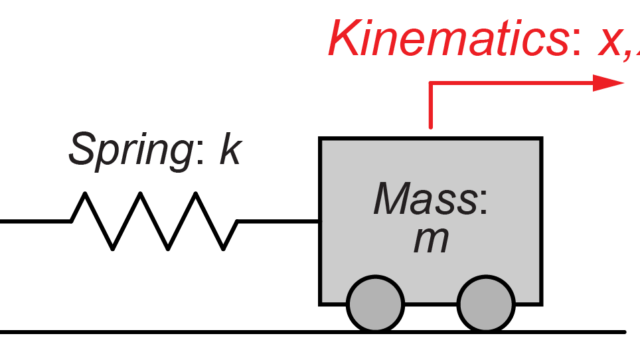
今回はこちらのモデルを用いて、システムの運動を考えます。

質量$m$がばね$k$とダンパー$c$で壁に接続されています。

このシステムについて、力$f$が質量$m$に加わっている場合の運動を求めていきます。

システムの運動方程式

このシステムの運動方程式は、

$$ m = \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t) $$

となります。

この運動方程式の一般解は、

$$ x(t) = e^{-\frac{c}{2 m}t} \left( C_1 \cos \left( \sqrt{\frac{k}{m}-\left( \frac{c}{2 m} \right) ^2} t \right) + C_2 \sin \left( \sqrt{\frac{k}{m}-\left( \frac{c}{2 m} \right) ^2} t \right) \right) $$

$$ + K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) $$

となります。

この式について、前の部分

$$ e^{-\frac{c}{2 m}t} \left( C_1 \cos \left( \sqrt{\frac{k}{m}-\left( \frac{c}{2 m} \right) ^2} t \right) + C_2 \sin \left( \sqrt{\frac{k}{m}-\left( \frac{c}{2 m} \right) ^2} t \right) \right) $$

は初期値に対する過度解で、後ろの部分

$$ K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) $$

は定常解になります。

今回は、初期条件を$x(0)=0$で$\dot{x}(0)=0$として、定常解のみ考慮していきたいと思います。

定常解を求める

システムの定常解$x(t)$を

$$ x(t) = K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) $$

とすると、速度$\dot{x}(t)$および加速度$\ddot{x}(t)$は$x(t)$を時間$t$で微分して、

$$ \dot{x}(t) = K_1 \omega \cos \left( \omega t \right) – K_2 \omega \sin \left( \omega t \right) $$

$$ \ddot{x}(t) = – K_1 \omega^2 \sin \left( \omega t \right) – K_2 \omega^2 \cos \left( \omega t \right) $$

と求めることが出来ます。

この各値を運動方程式に代入して、各値を求めていきます。

今回、入力する力$f$は、

$$ f(t) = F_0 \sin \left( \omega t \right) $$

とします。

実際に運動方程式に代入すると、

$$ m \left[ – K_1 \omega^2 \sin \left( \omega t \right) – K_2 \omega^2 \cos \left( \omega t \right) \right] $$

$$+c \left[ K_1 \omega \cos \left( \omega t \right) – K_2 \omega \sin \left( \omega t \right) \right] $$

$$+ k \left[ K_1 \sin \left( \omega t \right) + K_2 \cos \left( \omega t \right) \right] = F_0 \sin \left( \omega t \right)$$

となります。

この運動方程式を$\sin$成分と$\cos$成分に分けて整理すると、

$$ \begin{bmatrix} k – m \omega^2 & -c \omega \\ c \omega & k – m \omega^2 \end{bmatrix} \begin{bmatrix} K_1 \\ K_2 \end{bmatrix} = \begin{bmatrix} F_0 \\ 0 \end{bmatrix} $$

と行列式で表すことが出来ます。

これの式を$K_1$と$K_2$について解くと、システムの一般解$x(t)$を得ることが出来ます。

$$ K_1 = F_0 \frac{k – m \omega^2}{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2} $$

$$ K_2 = F_0 \frac{- c \omega}{\left( k – m \omega^2 \right)^2 + \left( c \omega \right)^2} $$