自動運転車を制御してみよう：車の運動力学モデルを求める

本シリーズでは、車やロボットの自動運転を実際に行うために必要となる制御工学の情報を紹介していきます。

自動運転車を制御してみよう 本シリーズでは、実際に車やロボットの自動運転を行うために必要な制御工学の情報を紹介していきます。 今回は、本シリー...

今回は、本シリーズで取り扱う車の運動力学モデルを算出する方法を紹介していきます。

４輪車モデルと２輪車モデル

自動運転車を制御するために、取り扱う車の運動力学モデルを得る必要があります。

この車のモデルについて、４輪車モデルと２輪車モデルについて紹介します。

４輪車モデルについて

まず、一般的に車と聞いて思い浮かべる４輪車のモデルを考えます。

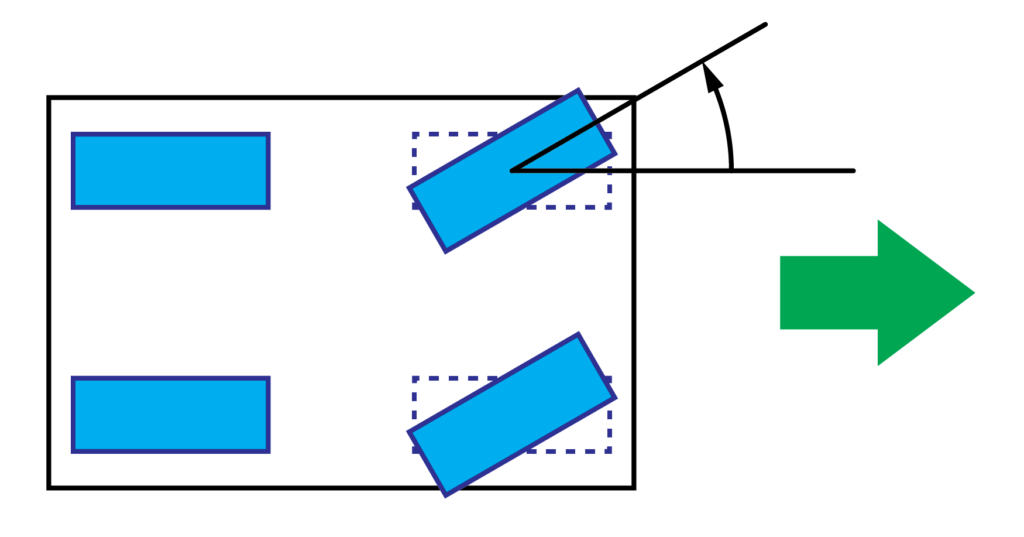
図のように、２つの後輪は常に進行方向（前：緑矢印）を向いています。

また、２つの前輪はハンドル（ステアリング）によって角度が変化します。

このように、前輪の角度が進行方向に対して変化することで車の進行方向を変えることが出来ます。

２輪車モデルについて

次に、自転車のような２輪車のモデルについて考えます。

２輪車モデルの場合でも、基本的には４輪車モデルと同様に考えることが出来ます。

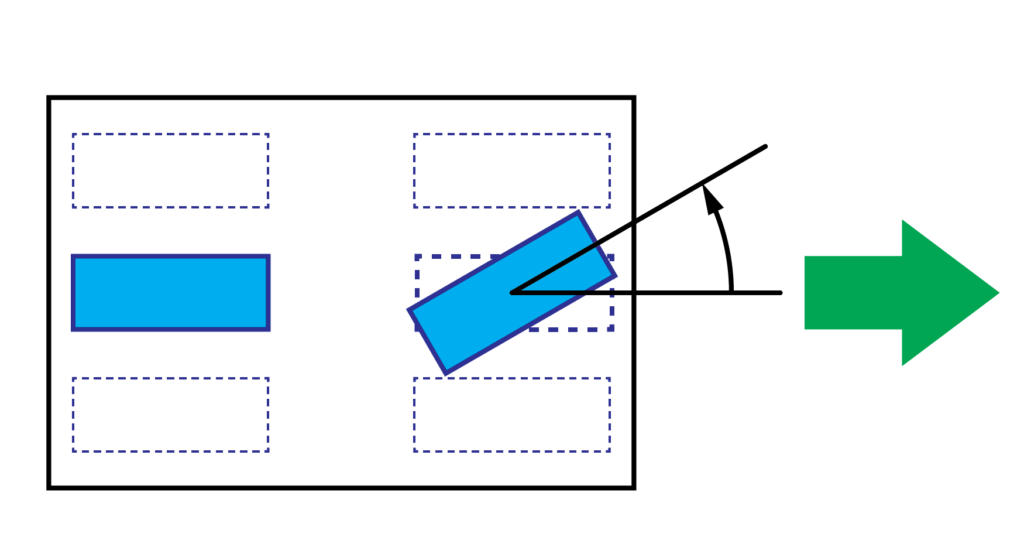
図のように、後輪の角度は常に固定で、前方（進行方向：緑矢印）を向いています。

そして、前輪の角度はハンドル（ステアリング）によって変化します。

この結果、２輪車の進行方向を前輪の角度によって変化させることが出来ます。

本シリーズでは、比較的簡単に考えることが出来る２輪車モデルを用いて自動運転車の制御を考えていきます。

２輪車モデルでの自動運転車が実現できるようになれば、そこから４輪車モデルに変更する事は簡単だと思います。

運動力学モデル

本シリーズで取り扱う２輪車モデルについて、車の位置と進行方向の変化を求めるために運動力学モデルを求めていきます。

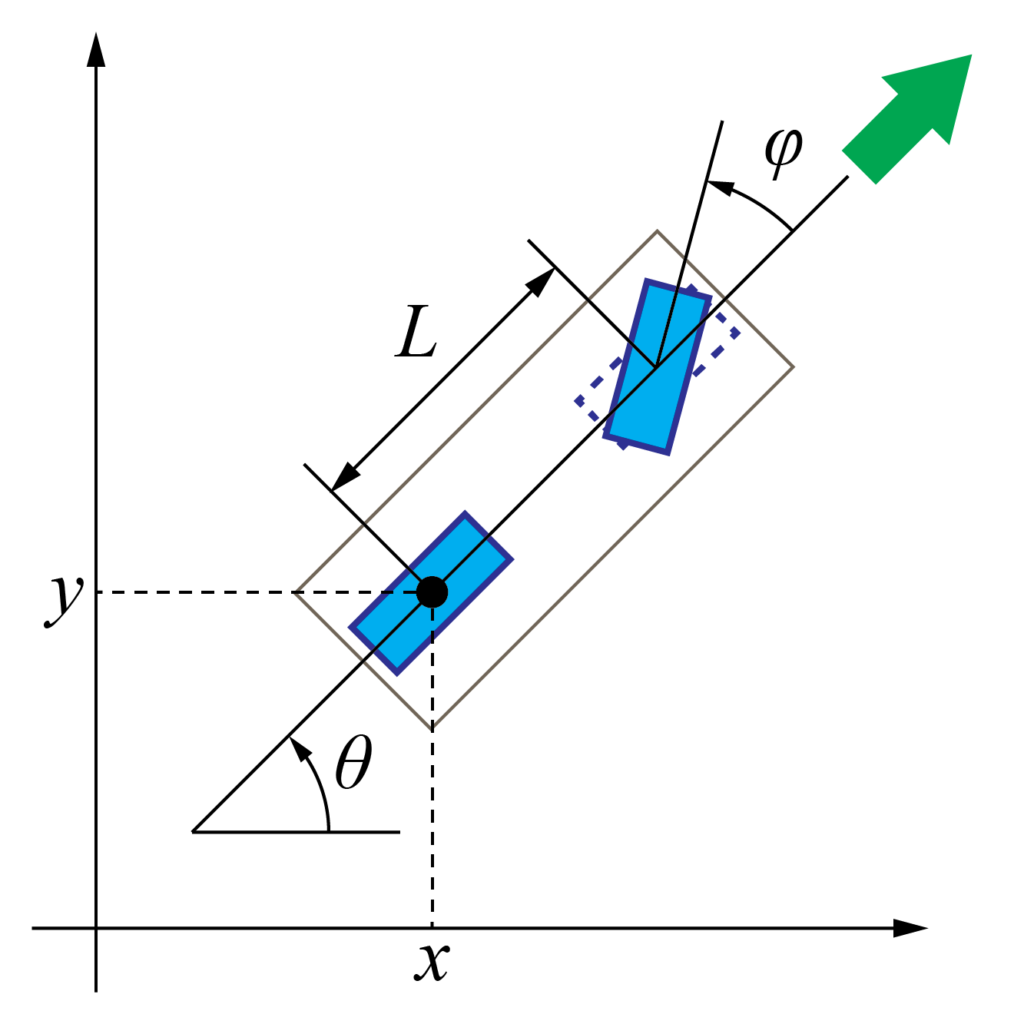
位置の変化を求める

車の位置の変化を求めるために、車の速度と進行方向との関係を数式で表していきます。

車の速度を\(v \ [m/sec]\)、進行方向を\(\theta \ [rad]\)とすると、平面上の各軸（X軸とY軸）についての速度（\(\dot{x} \ [m/sec]\)と\(\dot{y} \ [m/sec]\)）は

$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{x} = v \cos \theta \\ \dot{y} = v \sin \theta \end{array} \right. \end{eqnarray} $$

と表すことが出来ます。

この２式は、車の速度\(v\)を三角関数（\(\sin\)や\(\cos\)）を用いて各軸に分配することで各軸の速度（\(\dot{x}\)と\(\dot{y}\)）を求めています。

ちなみに・・・

微小時間\(\Delta t\)での車の移動（位置の変化）について考えます。

微小時間\(\Delta t\)では、車の進行方向\(\theta\)はハンドルによってほとんど変化しないと考えることが出来ます。

この微小時間\(\Delta t\)で車が移動する各軸の移動距離をそれぞれ\(\Delta x\)と\(\Delta y\)とすると、この各軸の移動距離と車の進行方向\(\theta\)は

$$ \frac{\Delta y}{\Delta x} = \tan \theta $$

という関係を導くことが出来ます。

ここで、微小時間\(\Delta t\)での各軸の移動距離（\(\Delta x\)と\(\Delta y\)）について

$$ \frac{\Delta y}{\Delta x} = \frac{\frac{\Delta y}{\Delta t}}{\frac{\Delta x}{\Delta t}} = \frac{\dot{y}}{\dot{x}} $$

の関係性があります。

また、三角関数の基本的な公式より

$$ \tan \theta = \frac{\sin \theta}{\cos \theta} $$

という式が得られます。

よって、最初の式に後２つの式を代入すると

$$ \frac{\dot{y}}{\dot{x}} = \frac{\sin \theta}{\cos \theta} $$

となります。

この式を整理することで

$$ – \dot{x} \cdot \sin \theta + \dot{y} \cdot \cos \theta = 0 $$

という関係式を導くことが出来ました。

ここで、先ほど求めた

$$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{x} = v \cos \theta \\ \dot{y} = v \sin \theta \end{array} \right. \end{eqnarray} $$

を関係式に代入すると

$$ – v \cos \theta \cdot \sin \theta + v \sin \theta \cdot \cos \theta = 0 $$

となり、先に求めた各軸の速度の式（\(\dot{x}\)と\(\dot{y}\)）が成り立つことが分かりました。

進行方向の変化を求める

次に、車の進行方向の変化を求めていきます。

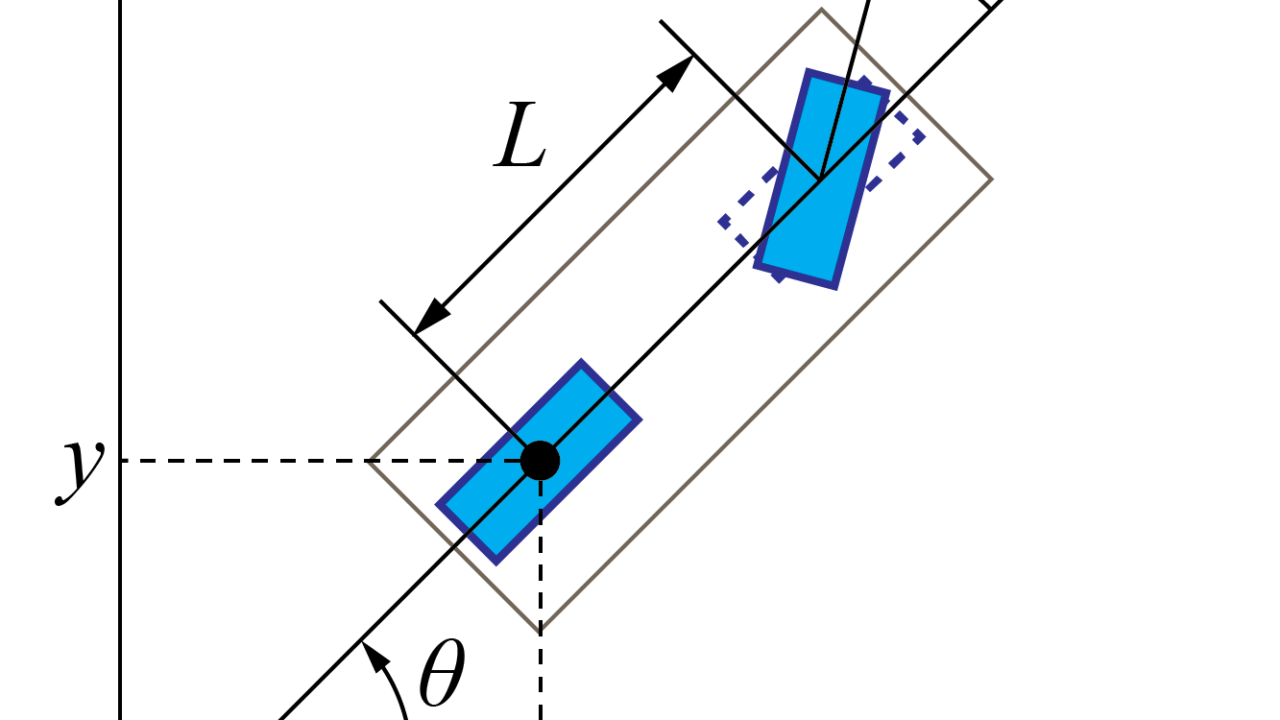
微小時間\(\Delta t\)での車の移動距離（位置の変化）を\(\Delta s\)、車の進行方向の変化を\(\Delta \theta\)とすると

$$ \Delta \theta \cdot \rho = \Delta s $$

という関係式を導くことが出来ます。

ここで、\(\rho\)は車の回転半径を示しています。

この回転半径\(\rho\)が小さいと車は小回りし、回転半径\(\rho\)が大きいと大回りでゆっくりと車の進行方向が変化します。

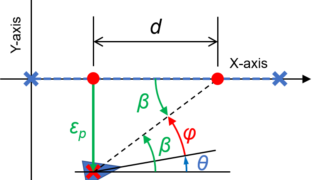
ここで、ハンドル（ステアリング）の角度\(\phi\)と回転半径\(\rho\)の関係は、車の前輪と後輪との間の距離\(L\)を用いて、

$$ \begin{eqnarray} \tan \phi = \frac{L}{\rho} \\ \Rightarrow \rho = \frac{L}{\tan \phi} \end{eqnarray} $$

と表すことが出来ます。

この求めた回転半径\(\rho\)の式を最初の関係式に代入して整理すると

$$ \begin{eqnarray} \Delta \theta \rho &=& \Delta s \\ \Delta \theta &=& \frac{\Delta s}{\rho} \\ &=& \frac{\Delta s \cdot \tan \phi}{L} \end{eqnarray} $$

のように、進行方向の微小変化\(\Delta \theta\)を求める式が得られました。

この式の両辺について、微小時間\(\Delta t\)で割ると

$$ \frac{\Delta \theta}{\Delta t} = \frac{\Delta s}{\Delta t} \frac{\tan \phi}{L} $$

となります。

ここで、

$$ \begin{eqnarray} \dot{\theta} &=& \frac{\Delta \theta}{\Delta t} \\ v &=& \frac{\Delta s}{\Delta t} \end{eqnarray} $$

という関係より、進行方向の時間変化（ハンドルの角速度）\(\dot{\theta}\)は

$$ \dot{\theta} = \frac{v}{L} \tan \phi $$

と求めることが出来ました。

まとめ

今回は、車やロボット等の自動運転を実際するために、車の運動力学モデルを算出する方法を紹介しました。

本記事で算出した運動力学モデルを用いることで、単位時間当たりの車の位置や進行方向の変化を求めることが出来ます。

次回は、今回求めた２輪車の運動力学モデルを使って、シンプルな自動運転車の制御を行いたいと思います。

自動運転車を制御してみよう：簡単な制御モデルを求める 本シリーズは、実際に車やロボットの自動運転を行うために、必要な制御工学の情報を紹介しています。 https://tajim...