本シリーズは、車やロボットの自動運転を実現するために、必要となる制御工学の情報を紹介しています。
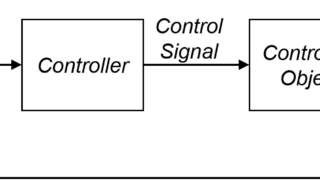
前々回、前回の記事では、車の運動力学モデルを求めて、車の位置と目標軌跡との誤差を算出する方法を紹介しました。
今回は、算出した誤差を基に簡単な自動運転モデルの制御する方法を紹介していきます。
簡単化した自動運転モデルと誤差の算出
前回までに紹介した自動運転モデルと誤差の算出方法を紹介します。
詳しい算出方法はこちらの記事を参考にしてください。
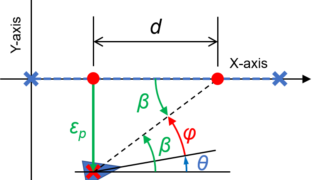
X-Y平面上で表された自動運転車を制御するために、ひとまず問題をシンプルにして目標の軌跡がX軸上のみに存在する場合を考えます。
このような目標軌跡を追従する車を自動制御するために、現在位置と目標軌跡との誤差\(\varepsilon_p\)を
$$ \varepsilon_p = y $$
という計算式で求めます。
この誤差\(\varepsilon_p\)を用いて、車のハンドル角度\(\phi\)を求めていきます。
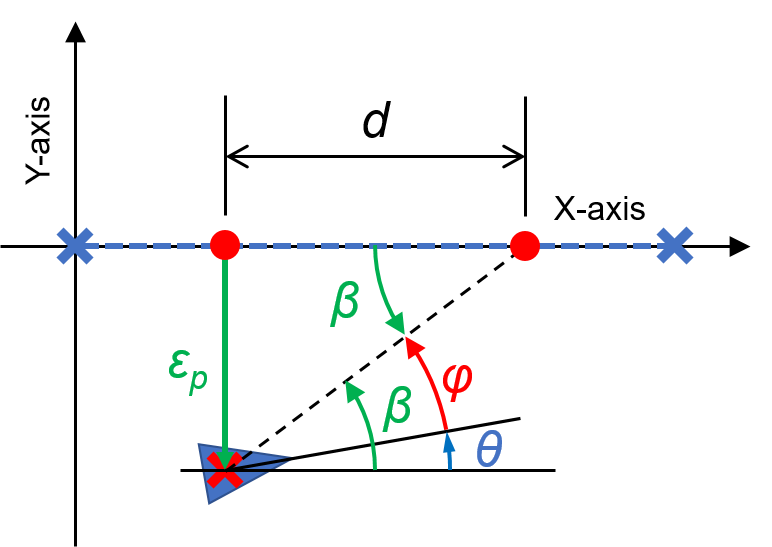
車の現在位置と目標軌跡との誤差\(\varepsilon_p\)から、目標となる車の進行方向\(\beta\)は
$$ \beta = \arctan \left( \frac{\varepsilon_p}{d} \right) $$
と求めることが出来ます。
この求めた目標の進行方向\(\beta\)に車の進行方向\(\theta\)を近づけるために、車のハンドルの角度\(\phi\)を
$$ \phi = \beta – \theta $$
と求めて車を制御します。
今回の記事では、この車を制御するためのハンドルの角度\(\phi\)を算出する際に、比例定数を用いて自動運転車の制御を行いたいと思います。
比例定数を用いた自動運転車の制御
今回は比例定数\(K\)を用いて自動運転車の制御を行います。
前回の記事で少しだけ紹介しましたが、車の進行方向\(\beta\)を求める式に含まれる距離\(d\)を変化させることで、車が目標軌跡に近づける様子を変更することが出来ます。
今回はこの特徴を利用して、車の現在位置と目標軌跡との誤差\(\varepsilon_p\)から、目標軌跡に追従させるための車の進行方向\(\beta\)の式
$$ \beta = \arctan \left( \frac{\varepsilon_p}{d} \right) $$
について、距離\(d\)を1にする代わりに比例定数\(K\)を追加して
$$ \begin{eqnarray} \beta &=& \arctan \left( K_p \frac{\varepsilon_p}{1} \right) \\ &=& \arctan \left( K_p \varepsilon_p \right ) \end{eqnarray} $$
と式を書き換えます。
そして、求めた目標の進行方向\(\beta\)から車のハンドル角度\(\phi\)を
$$ \begin{eqnarray} \phi &=& \beta – \theta \\ &=& \arctan \left( K_p \varepsilon_p \right ) – \theta \end{eqnarray} $$
と求めることが出来ます。
この様に比例定数\(K\)を用いることで、自由に車が目標軌跡に近づく様子を制御することが可能になります。
比例定数\(K\)が大きい場合は、ハンドルの角度\(\phi\)が大きくなるので、早く目標軌跡に近づくようになります。
また、比例定数\(K\)が小さい場合は、算出されるハンドルの角度\(\phi\)が小さくなるので、目標軌跡に近づく様がゆっくりになります。
この求めた車のハンドル角度\(\phi\)を以前の記事で求めた車の運動力学モデルに代入することで車の位置や進行方向を得ることが出来ます。
詳しい運動力学モデルの算出方法はこちらの記事を参考にしてください。
自動運転制御のシミュレーション結果
紹介した比例定数\(K\)を用いた自動運転車の制御を実際にシミュレーションで検証していきたいと思います。
時刻\(t=0\)での車の初期位置を\([x,y]=[0,-1]\)）、進行方向を\(\theta = 0^{\circ}\)とした場合に、X軸上の目標軌跡を追従させるための制御を行います。
また、車の前輪と後輪の差は車の速度は\(10 \ [m/s]\)として、シミュレーション時のサンプリング時間は\(1 \ [msec] = 1 \ [kHz]\)とします。
このシミュレーション条件の際に、比例定数\(K\)を変化させた場合の自動運転車の制御の様子を比較します。
比例定数\(K=1\)の場合
比例定数\(K\)を1に設定して先程の条件下でシミュレーションを行いました。
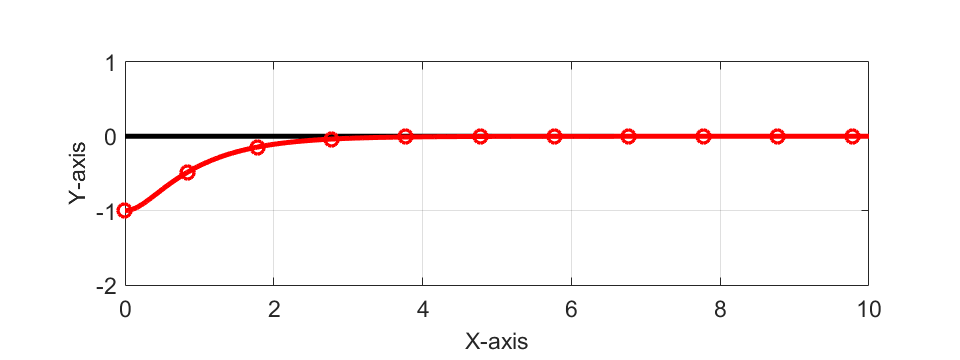
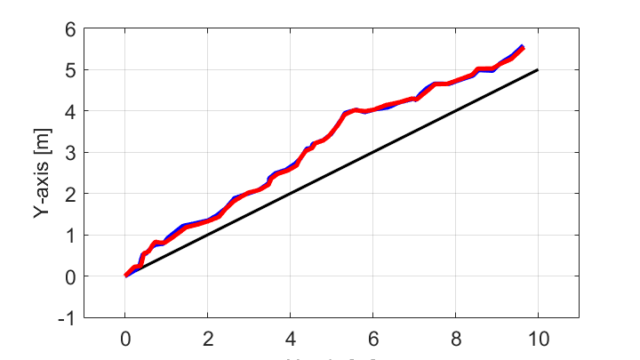
ここで、X軸上の黒線が目標軌跡、赤線が自動運転車の位置の軌跡を表しています。
また、赤の丸印は0.1[sec]ごとの車の位置を示しています。
シミュレーション結果から分かるように、シミュレーション開始時に存在した誤差\(\varepsilon_p\)が徐々に目標軌跡に近づいていることが分かります。
比例定数\(K=10\)の場合
次に比例定数を\(K=10\)と変更した場合の自動運転車の位置の軌跡を求めて、\(K=1\)の場合と比較していきたいと思います。
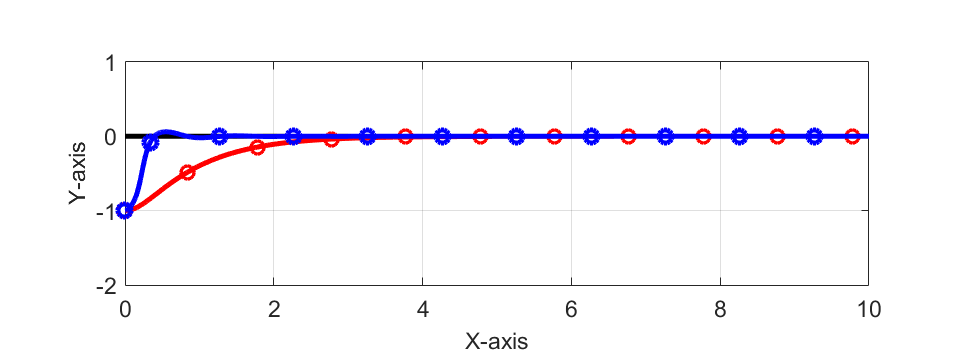
ここで、赤線が先程の\(K=1\)の時の結果で、青線が\(K=10\)の時の自動運転車の位置の軌跡を表しています。
シミュレーション結果より、比例定数\(K\)を1から10と大きくした場合、車が目標軌跡に近づく時間や距離が短くなっていることが分かります。
また、比例定数\(K=1\)の時と比べて、比例定数\(K=10\)の時の自動運転車の軌跡はマイナス側からプラス側に超えながら（オーバシュートしながら）目標に近づいていることが分かります。
さらに、比例定数\(K=10\)の時は車が目標軌跡に近づくための角度が急になる事から、X軸上を10[m]進むための時間は比例定数\(K=1\)の時と比較して多く掛かっています。
比例定数\(K=0.2\)の場合
次に比例定数を\(K=0.2\)と変更した場合の自動運転車の位置の軌跡を求めて、他の条件\(K=1,10\)の結果と比較していきます。
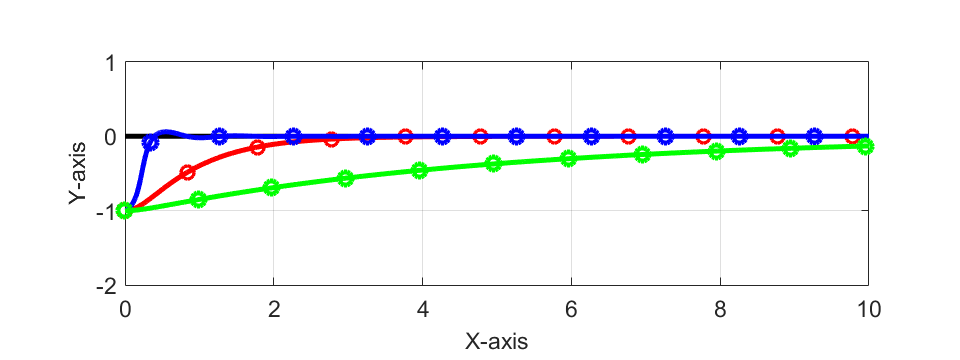
ここで、緑線が\(K=0.2\)の時の自動運転車の位置の軌跡を表しており、赤線が\(K=1\)、青線が\(K=10\)の時の自動運転車の位置の軌跡を表しています。
シミュレーション結果より、比例定数\(K\)を0.2と1から小さくした場合、車が目標軌跡に近づく時間や距離が長くなっていることが分かります。
これは、車を目標に近づけるためのハンドルの角度が比例定数\(K\)によって小さくなるためです。
これらの結果より、比例定数\(K\)を変更することで、自動運転車が目標軌跡を追従する様を制御することが出来ると分かりました。
まとめ
今回は、車やロボットの自動運転を実現する行うために、車と目標軌跡との誤差から自動運転車を制御する方法を紹介しました。
今回までの記事で紹介したように、難しく感じる自動運転車の制御も問題を分割して考えることで、比較的シンプルに行えることがわかると思います。
次回は、目標軌跡がX軸上のみではなく、X-Y平面上に存在する場合について考えていきたいと思います。
合わせて読みたい
実際にシミュレーションに用いたMATLABコードを紹介しています。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
