今回のシリーズでは、ロボットや自動運転車を制御する際にとても重要となる、ロボットや車の正確な位置を知る方法として、カルマンフィルタを用いたロボットの位置推定の方法を紹介しています。
前回の記事では、線形動的システムの自己位置推定問題を解くためにカルマンフィルタの基本的な式について説明しました。
今回からは、実際に線形な動的システムの例を用いて、カルマンフィルタを用いたロボットの自己位置推定を行いたいと思います。
前回までの復習
今回のシリーズ記事で取り扱っている移動ロボットの自己位置推定問題と線形動的システム、そして用いるカルマンフィルタについておさらいします。
自己位置推定問題
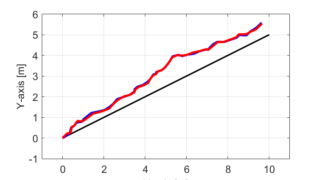
本シリーズでは、上の図で表されるように黒線の目標軌跡を入力として与えられた線形な動的システムの軌跡が、雑音（誤差）などによって青線のようにずれた場合について、カルマンフィルタを用いて赤線のようにロボットの自己位置を推定する問題を考えています。
線形動的システム
本シリーズで取り扱う線形動的システムの状態空間モデルは
$$ \begin{eqnarray} \boldsymbol{x}_t &=& \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t + \boldsymbol{w}_t \\ \boldsymbol{z}_t &=& \boldsymbol{H}_t \boldsymbol{x}_{t} + \boldsymbol{v}_t \end{eqnarray} $$
のように、入力や観測に雑音（wやv）
$$ \boldsymbol{w}_t \sim N \left( 0,\boldsymbol{Q}_t \right) $$
$$ \boldsymbol{v}_t \sim N \left( 0,\boldsymbol{R}_t \right) $$
が含まれているシンプルなモデルを考えます。
カルマンフィルタの基本式
カルマンフィルタは予測と更新の２つのステップで構成されています。
予測ステップは、1つ前の状態から現在の状態を予測するステップで、その基本式は
$$ \begin{eqnarray} \left\{ \begin{array} \hat{\boldsymbol{x}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{x}}_{t-1|t-1} + \boldsymbol{B}_t \boldsymbol{u}_t \\ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t \end{array} \right. \end{eqnarray} $$
で表されます。
更新ステップは、予測した状態と観測の情報を用いて現在の状態を更新するステップで、その基本式は
$$ \begin{eqnarray} \left\{ \begin{array} \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – \boldsymbol{H}_t \hat{\boldsymbol{x}}_{t|t-1} \\ \boldsymbol{S}_t = \boldsymbol{R}_t + \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T \\ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} \\ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t \\ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} \end{array} \right. \end{eqnarray} $$
と表されます。
カルマンフィルタによる自己位置推定
実際に具体的な値を用いながらカルマンフィルタによる線形動的システムの自己位置推定問題を解いていきます。
状態方程式と雑音の影響
今回の記事で取り扱う問題では、点[0,0]から点[10,5]までの直線を目標軌跡として移動ロボットに与えています。
これより、線形動的システムの状態方程式
$$ \boldsymbol{x}_t = \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t + \boldsymbol{w}_t $$
における入力utは各ステップ時間t毎に
$$ \boldsymbol{u}_t = \begin{bmatrix} 0.2 \\ 0.1 \end{bmatrix} $$
と各軸（X軸とY軸）に対する移動量を直接与えます
今回にシミュレーションでは、この入力を50ステップ時間の範囲でロボットに与えます。
そうすることで、雑音が存在しない場合にロボットは点[0,0]から点[10,5]までまっすぐ移動することになります。
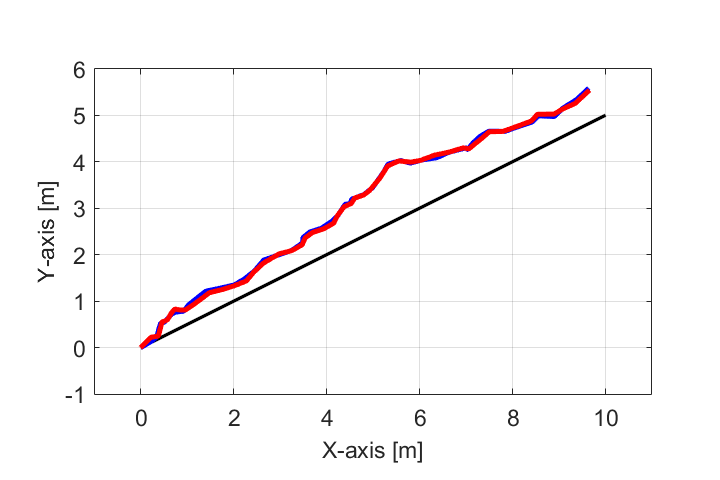
この入力utが与えられた場合の移動ロボットの状態方程式は
$$ \begin{bmatrix} x_t \\ y_t \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} 0.2 \\ 0.1 \end{bmatrix} + \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} $$
という形になります。
ここで、雑音を示すwtは
$$ \boldsymbol{w}_t \sim N \left( 0,0.2^2 \right) $$
のように正規分布に従って生じるノイズを表します。
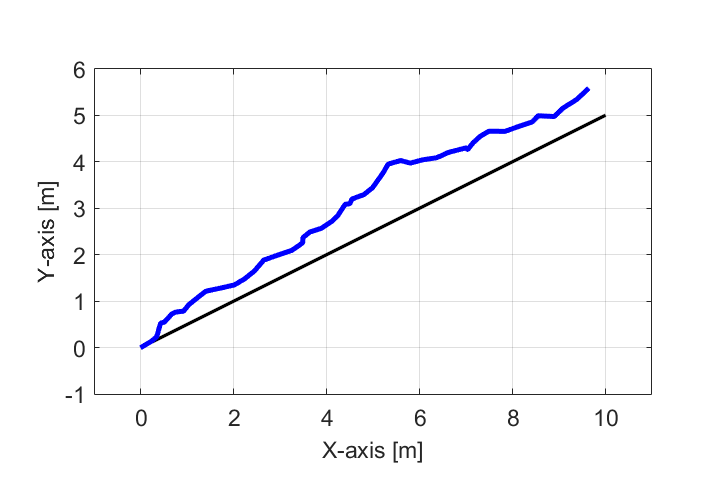
この雑音wの影響により、ロボットの実際の軌跡（青線）が目標軌跡（黒線）に対してズレていきます。
この状態方程式を表したMATLABのプログラムは下記の通りです。
function x = StateEquation(x,u,w) x = x + u + normrnd(0,w); end
出力方程式と雑音の影響
今回のシミュレーションでは、観測にGPSのようなX軸とY軸の値が直接得られるセンサを用いるとします。
この時のシステムの出力方程式は
$$ \begin{bmatrix} z_{x,t} \\ z_{y,t} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} $$
と表すことが出来ます。
この時の雑音vtは
$$ \boldsymbol{v}_t \sim N \left( 0,0.3^2 \right) $$
のように正規分布に従って発生するノイズを表しています。
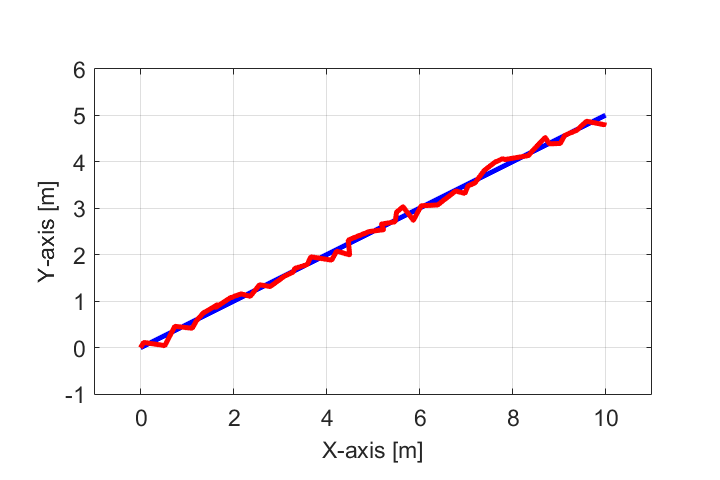
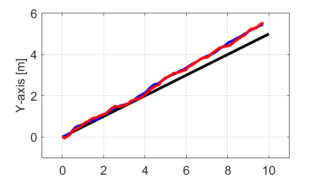
この観測に関する雑音vによる影響で、たとえロボットの軌跡（青線）が目標軌跡上を正確に移動していたとしても、観測による得られる現在位置の情報（赤線）は目標軌跡（青線）からズレが生じます。
このように入力にも出力にも雑音を含んだ線形動的システムに対して、カルマンフィルタを用いたロボットの自己位置推定を行います。
この出力方程式を表したMATLABのプログラムは下記の通りです。
function z = OutputEquation(x,v) z = x + normrnd(0,v); end
まとめ
今回は、カルマンフィルタを用いたロボットの自己位置推定を行うために、取り扱う線形な動的システムの例を説明しました。
今回紹介したように、入力と出力に含まれる雑音（誤差）の影響により、実際のロボットの軌跡は目標軌跡から外れてしまいます。
ほとんどの現実世界のロボットの入力と出力には雑音が含まれており、ロボットの現在位置を把握することはとても重要な問題です。
次回は、この雑音を含んだ線形動的システムについてカルマンフィルタを用いて自己位置を推定していきます。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
