非線形動的システムの状態空間モデル：カルマンフィルタでロボットの位置推定をしてみよう（６）

今回のシリーズでは、ロボットや自動運転車を制御する際に重要な、ロボットや車の正確な位置を得る方法として、カルマンフィルタを用いたロボットの位置推定の方法を紹介しています。

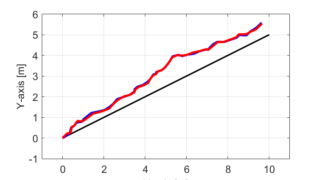
カルマンフィルタでロボットの位置推定をしてみよう！ロボットや自動運転車を制御するときに、ロボットや車の正確な位置を知ることはとても重要です。しかし、ロボットを制御...

前回の記事では、非線形動的システムの自己位置推定を行うために、拡張カルマンフィルタを用いる手法を紹介しました。

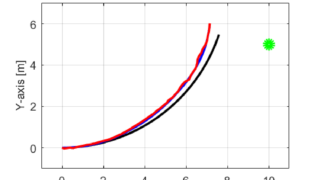
拡張カルマンフィルタって何？：カルマンフィルタでロボットの位置推定をしてみよう（５）今回のシリーズでは、自動運転車や移動ロボットを制御するためにとても重要な正確な位置を知る方法として、カルマンフィルタを用いたロボ...

今回の記事では、実際に拡張カルマンフィルタを用いて移動ロボットの自己位置推定を行うために、非線形なシステムであるロボットを非線形動的システムの状態空間モデルで表していきたいと思います。

Contents

取り扱う自己位置推定問題
非線形動的システムの状態空間モデル
- 状態方程式
- 出力方程式
まとめ

取り扱う自己位置推定問題

今回からの拡張カルマンフィルタを用いた自己位置推定を行う環境を説明します。

今回は、移動ロボットとして対向２輪型の車輪ロボットを取り扱います。

対向２輪型のロボットの詳細については、こちらの記事を参考にしてください。

車輪ロボット（対向2輪型）の運動を計算してみよう今回は車輪ロボットとして対向2輪型ロボットの運動を取り扱いたいと思います。車輪ロボットの中でもシンプルな構造なので、移動...

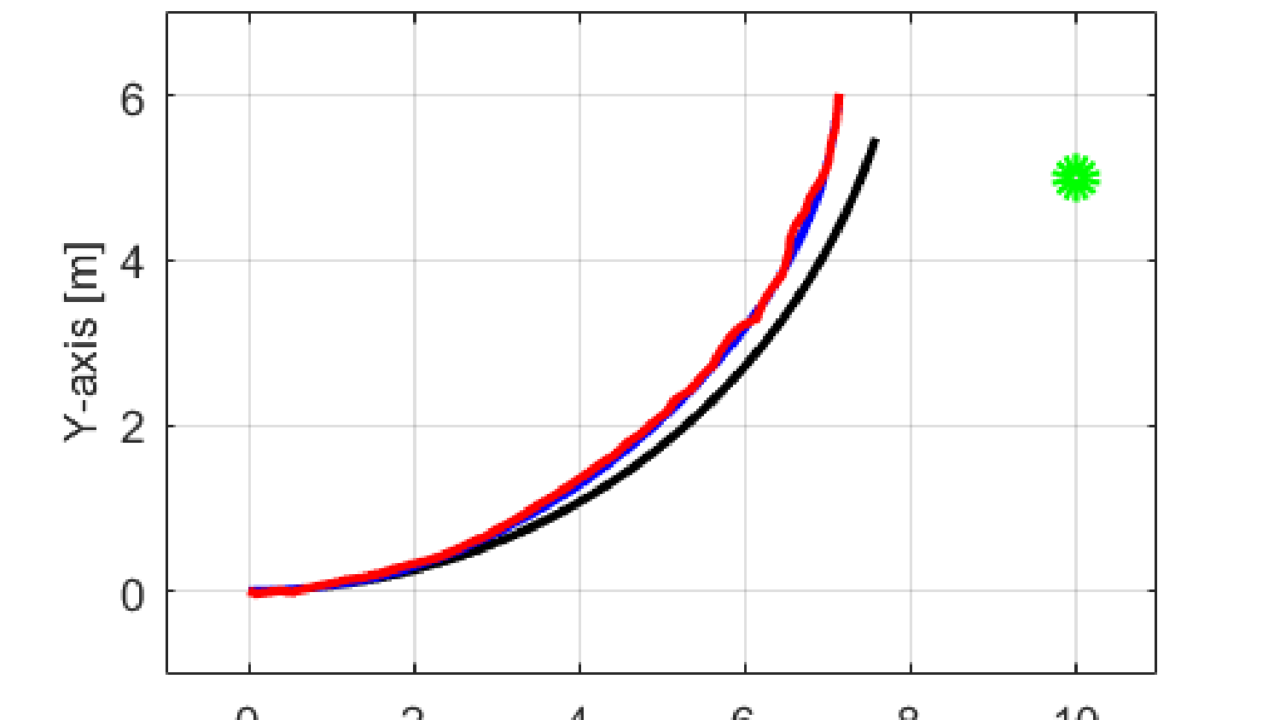
ロボットは平面上の点[0,0]を始点とし、徐々に左に曲がりながら円を描いていきます。

しかし、実際にはロボットの右側と左側の車輪にそれぞれ与えられる入力信号には誤差が生じるため、目標通りにきれいな円を描くことはできません。

そこで、ロボットの現在位置を把握するために距離センサを用います。

平面上の点に存在するマーカーとの距離とその角度から現在の位置を把握します。

しかし、このセンサの出力にも誤差が生じるために、実際にはセンサの値のみで正確な位置を把握することは難しくなります。

この様な問題において、ロボットの自己位置をより正確に推定するために、拡張カルマンフィルタを用いた自己位置推定を行います。

非線形動的システムの状態空間モデル

取り扱う非線形システムの移動ロボットについて、拡張カルマンフィルタを用いるために状態空間モデルで表していきます。

今回の記事で用いる非線形動的システムの状態空間モデルの基本式は

$$ \begin{eqnarray} \boldsymbol{x}_t &=& f \left( \boldsymbol{x}_{t-1}, \boldsymbol{u}_t , \boldsymbol{w}_t \right) \\ \boldsymbol{z}_t &=& h \left( \boldsymbol{x}_{t} \right) + \boldsymbol{v}_t \end{eqnarray} $$

と表します。

状態方程式

対向２輪型の車輪ロボットについて、時刻tでの状態と入力信号uから時刻t+1での状態を算出するために、状態方程式を求めていきます。

今回取り扱う移動ロボットの状態は、ロボットの位置（X軸とY軸）と姿勢

$$ \begin{eqnarray} \begin{bmatrix} x \\ y \\ \theta \end{bmatrix} \end{eqnarray} $$

で構成されています。

両車輪に与える入力信号をuとして、この入力信号に対する雑音をwとすると、右側と左側の車輪に与える入力信号u_Rとu_Lは

$$ \begin{eqnarray} \begin{bmatrix} u_R \\ u_L \end{bmatrix} &=& \boldsymbol{u} + \boldsymbol{w} \\ &=&\begin{bmatrix} u(1) \\ u(2) \end{bmatrix} + \begin{bmatrix} w(1) \\ w(2) \end{bmatrix} \end{eqnarray} $$

となります。

この右側と左側の車輪に与える入力信号（u_Rとu_L）と両車輪間の距離dから、この時の移動ロボットの速度vと角速度ωは

$$ \begin{eqnarray} v &=& (v_R+v_L)/2 \\ \omega &=& (v_R-v_L)/2d \end{eqnarray} $$

と求めることが出来ます。

これより、現在の時刻tと求める時刻t+1との差をΔtとすると、今回の対向２輪型ロボットの状態方程式は

$$ \begin{eqnarray} x_{t+1} &=& x_t + v \Delta t \cos \left(\theta_t + \omega \Delta t / 2\right) \\ y_{t+1} &=& y_t + v \Delta t \sin \left(\theta_t + \omega \Delta t / 2\right) \\ \theta_{t+1} &=& \theta_t + \omega \Delta t \end{eqnarray} $$

のようになり、時刻t+1での状態が時刻tの状態と入力信号u（雑音wを含む）から求められる速度vと角速度ωから算出できるようになりました。

出力方程式

今回の動作環境では、センサはロボットは現在の状態（位置と角度）から見たマーカー（目印）までの距離と角度を出力します。

また今回の条件では、このマーカーの位置LM（X軸とY軸）は予め知っている（分かっている）として

$$ \boldsymbol{LM} = \begin{bmatrix} LM(1) \\ LM(2) \end{bmatrix} $$

で表します。

ここで、LM(1)がX軸成分でLM(2)がY軸成分を表しています。

よって、このマーカーの位置LMと現在のロボットの位置（xとy）と角度θから、センサの出力（距離と角度）を求めると

$$ \begin{eqnarray} \boldsymbol{z_t} &=& \begin{bmatrix} z_t(1) \\ z_t(2) \end{bmatrix} \\ &=& \begin{bmatrix} \sqrt{(LM(1)-x_t)^2+(LM(2)-y_t)^2} \\ \arctan{\left( \frac{LM(2)-y_t}{LM(1)-x_t} \right)} – \theta_t \end{bmatrix} \end{eqnarray} $$

となります。

このセンサの出力zの距離と角度にも雑音vが含まれます。

よって、この雑音vの影響を考慮すると、今回のシステムの出力方程式は

$$ \begin{eqnarray} z_t (1) &=& \sqrt{(LM(1)-x_t)^2+(LM(2)-y_t)^2} + v(1) \\ z_t (2) &=& \arctan{\left( \frac{LM(2)-y_t}{LM(1)-x_t} \right)} – \theta_t + v(2) \end{eqnarray} $$

となり、現在の状態（位置x,yと向きθ）とマーカーLMの位置、そして含まれる誤差vで表すことが出来ます。