今回のシリーズでは、自動運転車や移動ロボットを制御するためにとても重要な正確な位置を知る方法として、カルマンフィルタを用いたロボットの位置推定の方法を紹介しています。
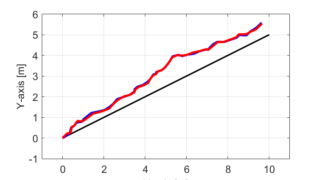
これまでの記事では、線形動的システムに対してカルマンフィルタを用いて自己位置推定を行いました。
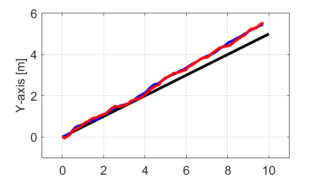
しかし、世の中のシステムには非線形な動的システムが多く存在します。
今回からの記事では、この様な非線形動的システムの自己位置推定を行うために、拡張カルマンフィルタを用いる手法を紹介していきます。
線形動的システムとカルマンフィルタ
前回までの記事で取り扱っていた線形動的システムとカルマンフィルタの基本式についておさらいします。
線形動的システム
線形動的システムは、その名の通り線形で動的なシステムです。
線形動的システムの状態空間モデルは
$$ \begin{eqnarray} \boldsymbol{x}_t &=& \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t + \boldsymbol{w}_t \\ \boldsymbol{z}_t &=& \boldsymbol{H}_t \boldsymbol{x}_{t} + \boldsymbol{v}_t \end{eqnarray} $$
のように線形な式で表すことが出来ます。
また上の式中に含まれるwとvは、入力や観測の雑音を表しています。
詳しくは、こちらの記事を参考にしてください。

カルマンフィルタの基本式
この線形な動的システムについてロボットの自己位置推定を行うために、カルマンフィルタを用います。
カルマンフィルタには、
- 予測ステップ
- 更新ステップ
の2つのステップがあります。
カルマンフィルタの予測ステップにおける基本式は
$$ \begin{eqnarray} \left\{ \begin{array} \hat{\boldsymbol{x}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{x}}_{t-1|t-1} + \boldsymbol{B}_t \boldsymbol{u}_t \\ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t \end{array} \right. \end{eqnarray} $$
の2式で表されます。
また、カルマンフィルタの更新ステップにおける基本式は
$$ \begin{eqnarray} \left\{ \begin{array} \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – \boldsymbol{H}_t \hat{\boldsymbol{x}}_{t|t-1} \\ \boldsymbol{S}_t = \boldsymbol{R}_t + \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T \\ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} \\ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t \\ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} \end{array} \right. \end{eqnarray} $$
の5式で表されます。
詳しくは、こちらの記事を参考にしてください。

このカルマンフィルタを用いた移動ロボットの自己位置推定は、線形システムには有効ですが、非線形なシステムには適応することが出来ません。
そこで、このカルマンフィルタを少し拡張した、拡張カルマンフィルタを用いた非線形動的システムの自己位置推定を行いたいと思います。
非線形動的システム
まず、非線形な動的システムの状態空間モデルについて紹介します。
基本的な状態空間モデルの構成は線形動的システムの場合と同じで、状態方程式と出力方程式で表されます。
非線形動的システムの状態空間モデルは
$$ \begin{eqnarray} \boldsymbol{x}_t &=& f \left( \boldsymbol{x}_{t-1}, \boldsymbol{u}_t \right) + \boldsymbol{w}_t \\ \boldsymbol{z}_t &=& h \left( \boldsymbol{x}_{t} \right) + \boldsymbol{v}_t \end{eqnarray} $$
のようになり、非線形の関数であるfやhを用いて構成されています。
このように関数fやhのような非線形関数を含んでいるので、このような状態空間モデルで表されるシステムを非線形システムとなります。
また、線形動的システムの所で紹介した状態空間モデルの2式は、この関数fやhが線形な場合と同様の式を表しています。
上の式での非線形動的システムの状態空間モデルでは、入力や観測に対する雑音(wやv)が非線形関数fやhに含まれずに後から加えられていますが、取り扱うシステムによっては
$$ \begin{eqnarray} \boldsymbol{x}_t &=& f \left( \boldsymbol{x}_{t-1}, \boldsymbol{u}_t , \boldsymbol{w}_t \right) \\ \boldsymbol{z}_t &=& h \left( \boldsymbol{x}_{t} , \boldsymbol{v}_t \right) \end{eqnarray} $$
のように非線形関数fやh内に含まれる場合もあります。
この様な非線形な状態空間モデルで表される非線形動的システムの自己位置推定を行うために、拡張カルマンフィルタを用いていきます。
拡張カルマンフィルタ
拡張カルマンフィルタは、カルマンフィルタを非線形システムに対応するように拡張したものです。
ただ、拡張カルマンフィルタの基本的な形はカルマンフィルタと同じなので、カルマンフィルタが理解できていれば、拡張カルマンフィルタの理解もし易いと思います。
拡張カルマンフィルタは、カルマンフィルタの場合と同様に
- 予測ステップ
- 更新ステップ
の2つのステップで構成されています。
予測ステップ
予測ステップでは、1つ前の状態から現在の状態を予測します。
この予測ステップでは、推定状態xの予測\(\hat{\boldsymbol{x}}\)とその推定状態の確からしさを示す誤差共分散Pの予測\(\hat{\boldsymbol{P}}\)を行います。
推定状態の予測
時刻tでの推定状態xの予測\(\hat{\boldsymbol{x}}_{t|t-1}\)は、時刻t-1での推定状態と状態方程式を用いて
$$ \hat{\boldsymbol{x}}_{t|t-1} = f \left( \hat{\boldsymbol{x}}_{t-1|t-1} , \boldsymbol{u}_t \right) $$
と求めることが出来ます。
この推定状態を予測する際には実際には含まれるであろう雑音wによる影響は無視しています。
この雑音wによる影響は誤差共分散Pを算出する際に考慮していきます。
誤差共分散の予測
先程述べたように、雑音wによる影響を考慮して誤差共分散Pを予測していきます。
予測した誤差共分散\(\hat{\boldsymbol{P}}_{t|t-1}\)は
$$ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t $$
と求めることが出来ます。
ここで、式中に含まれる\(\boldsymbol{F}_t\)は
$$ \boldsymbol{F}_t = \left. \frac{\partial f}{\partial \boldsymbol{x}} \right| _{\hat{\boldsymbol{x}}_{t-1|t-1} , \boldsymbol{u}_t} $$
のように、状態方程式で用いている非線形関数fのヤコビアンで定義した行列です。
小まとめ
この2つの式
$$ \begin{eqnarray} \left\{ \begin{array} \hat{\boldsymbol{x}}_{t|t-1} = f \left( \hat{\boldsymbol{x}}_{t-1|t-1} , \boldsymbol{u}_t \right) \\ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t \end{array} \right. \end{eqnarray} $$
が拡張カルマンフィルタの予測ステップにおける基本式です。
更新ステップ
更新ステップでは、予測ステップで予測した状態と観測による情報から現在の状態を更新します。
この更新ステップでは、時刻t-1の状態から予測した推定状態xと誤差共分散Pに、観測により得られる情報zを加えて現在の時刻tでの推定状態を求めていきます。
観測残差の算出
まず、実際に観測により得られた情報zと今の推定状態なら得られるであろう情報との差を示す観測残差\(\tilde{\boldsymbol{y}}\)を求めます。
$$ \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – h \left(\hat{\boldsymbol{x}}_{t|t-1} \right) $$
観測残差の共分散を算出
そして、観測残差\(\tilde{\boldsymbol{y}}\)に対する誤差共分散\(\boldsymbol{S}\)を求めます。
$$ \boldsymbol{S}_t = \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T + \boldsymbol{R}_t $$
この時、式中に含まれる\(\boldsymbol{H}_t\)は
$$ \boldsymbol{H}_t = \left. \frac{\partial h}{\partial \boldsymbol{x}} \right| _{\hat{\boldsymbol{x}}_{t|t-1}} $$
と、出力方程式で用いられている非線形関数hのヤコビアンで定義した行列です。
カルマンゲインの最適化
そして、求めた値(行列)を基に、カルマンゲインKの最適化を行います。
$$ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} $$
推定状態の更新
最後に、最適化したカルマンゲインKを用いて推定状態xを更新します。
$$ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t $$
誤差共分散の更新
そして、誤差共分散Pも併せて更新します。
$$ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} $$
小まとめ
これら5つの式
$$ \begin{eqnarray} \left\{ \begin{array} \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – h \left(\hat{\boldsymbol{x}}_{t|t-1} \right) \\ \boldsymbol{S}_t = \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T + \boldsymbol{R}_t \\ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} \\ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t \\ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} \end{array} \right. \end{eqnarray} $$
が拡張カルマンフィルタの更新ステップにおける基本式になります。
まとめ
今回は、非線形動的システムの自己位置推定を行うために、拡張カルマンフィルタについて紹介しました。
拡張カルマンフィルタの基本的な式はカルマンフィルタと同じなので、理解するのはそこまで難しくはないと思います。
次回からは、実際にこの拡張カルマンフィルタを用いて移動ロボットの自己位置推定を行いたいと思います。
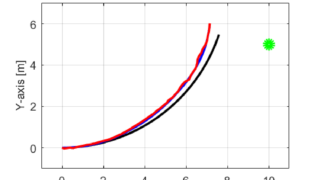




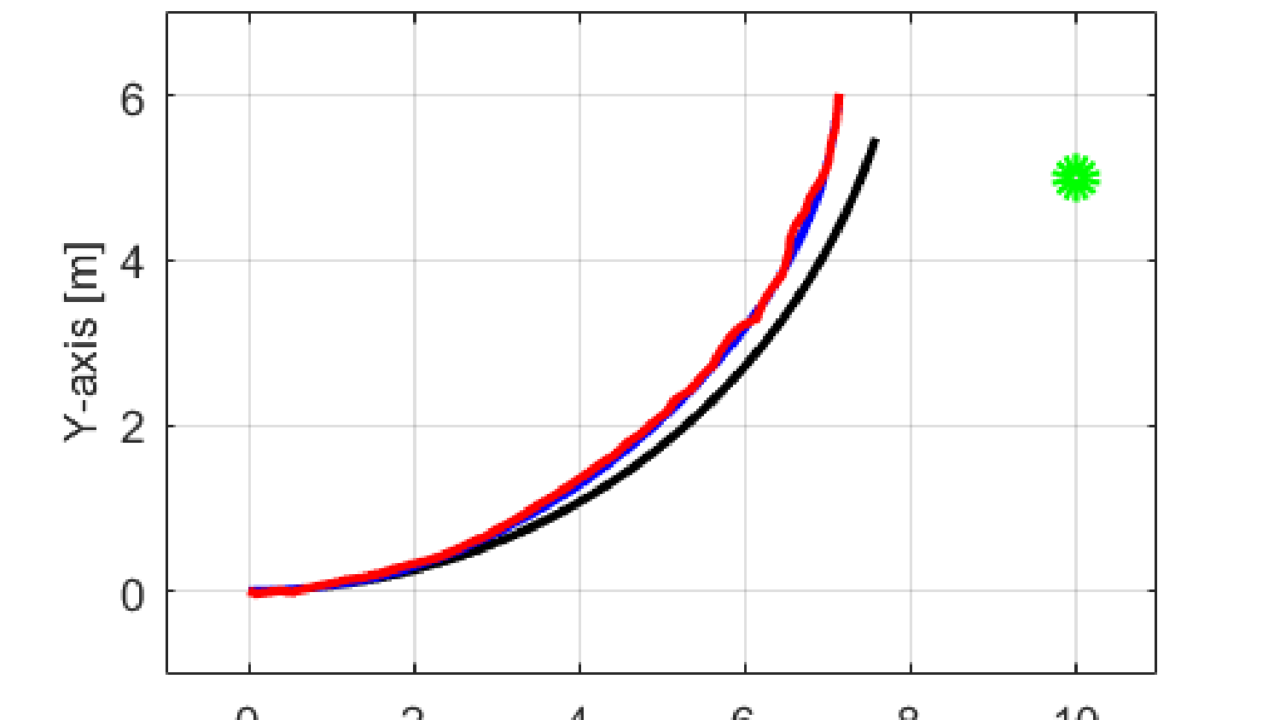




















 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
