シミュレーションで動作確認：カルマンフィルタでロボットの位置推定をしてみよう（４）

今回のシリーズでは、ロボットや自動運転車を制御する際に重要な、ロボットや車の正確な位置を得る方法として、カルマンフィルタを用いたロボットの位置推定の方法を紹介しています。

カルマンフィルタでロボットの位置推定をしてみよう！ ロボットや自動運転車を制御するときに、ロボットや車の正確な位置を知ることはとても重要です。 しかし、ロボットを制御...

前回の記事では、実際にカルマンフィルタを用いたロボットの自己位置推定を行うために、取り扱う線形動的システムの例を紹介しました。

カルマンフィルタと線形動的システム：カルマンフィルタでロボットの位置推定をしてみよう（３） 今回のシリーズでは、ロボットや自動運転車を制御する際にとても重要となる、ロボットや車の正確な位置を知る方法として、カルマンフィル...

今回の記事では前回からの続きとして、カルマンフィルタを用いた移動ロボットの自己位置推定のアルゴリズムを実装して、シミュレーションで動作を確認していきたいと思います。

前回までのおさらい

前回までの記事で紹介した、線形動的システムとカルマンフィルタの基本式をおさらいします。

詳細な情報については、それぞれの記事のリンクを参考にしてください。

カルマンフィルタでロボットの位置推定をしてみよう！ ロボットや自動運転車を制御するときに、ロボットや車の正確な位置を知ることはとても重要です。 しかし、ロボットを制御...

カルマンフィルタの基本式：カルマンフィルタでロボットの位置推定をしてみよう（２） 今回のシリーズでは、ロボットや自動運転車を制御する際にとても重要となる、ロボットや車の正確な位置を知る方法として、カルマンフィル...

線形動的システム

今回のシリーズで取り扱う線形で動的なシステムの状態空間モデルをおさらいします。

入力がu_t与えられた場合の移動ロボットの状態方程式は

$$ \begin{bmatrix} x_t \\ y_t \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} 0.2 \\ 0.1 \end{bmatrix} + \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} $$

という形になります。

ここで、雑音を示すwは

$$ \boldsymbol{w}_t \sim N \left( 0,0.2^2 \right) $$

のように正規分布に従って生じるノイズを表します。

また、システムの出力方程式は

$$ \begin{bmatrix} z_{x,t} \\ z_{y,t} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} $$

と表すことが出来ます。

この時の雑音vは

$$ \boldsymbol{v}_t \sim N \left( 0,0.3^2 \right) $$

のように正規分布に従って発生するノイズを表しています。

今回は、この様な状態空間モデルで表される線形動的システムを取り扱います。

カルマンフィルタ

カルマンフィルタの予測ステップと更新ステップの基本式についておさらいします。

予測ステップは、1つ前の状態から現在の状態を予測するステップで、その基本式は

$$ \begin{eqnarray} \left\{ \begin{array} \hat{\boldsymbol{x}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{x}}_{t-1|t-1} + \boldsymbol{B}_t \boldsymbol{u}_t \\ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t \end{array} \right. \end{eqnarray} $$

で表されます。

更新ステップは、予測した状態と観測の情報を用いて現在の状態を更新するステップで、その基本式は

$$ \begin{eqnarray} \left\{ \begin{array} \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – \boldsymbol{H}_t \hat{\boldsymbol{x}}_{t|t-1} \\ \boldsymbol{S}_t = \boldsymbol{R}_t + \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T \\ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} \\ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t \\ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} \end{array} \right. \end{eqnarray} $$

と表されます。

今回は、このカルマンフィルタを用いて移動ロボットの自己位置推定の問題を考えていきます。

アルゴリズムの実装

今回のカルマンフィルタによる移動ロボットの自己位置推定問題のアルゴリズムは、

1. シミュレーションの初期条件を設定
2. カルマンフィルタの予測ステップ
3. カルマンフィルタの更新ステップ
4. 以降２と３を繰り返す

という流れになります。

初期条件

カルマンフィルタによる自己位置推定のシミュレーションを行うために、まず始めに必要となる様々な初期条件を定義します。

線形動的システムの状態空間モデル

$$ \begin{eqnarray} \left\{ \begin{array} \boldsymbol{x}_t &=& \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t + \boldsymbol{w}_t \\ \boldsymbol{z}_t &=& \boldsymbol{H}_t \boldsymbol{x}_{t} + \boldsymbol{v}_t \end{array} \right. \end{eqnarray} $$

について、今回のシリーズで取り扱う移動ロボットの状態空間モデル

$$ \begin{eqnarray} \left\{ \begin{array}{l} \begin{bmatrix} x_t \\ y_t \end{bmatrix} &=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} 0.2 \\ 0.1 \end{bmatrix} + \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} \\ \begin{bmatrix} z_{x,t} \\ z_{y,t} \end{bmatrix} &=& \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{t-1} \\ y_{t-1} \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \end{array} \right. \end{eqnarray} $$

から、行列FとH、そして入力uを

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{F} &=&  \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ \boldsymbol{H} &=&  \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\ \boldsymbol{u} &=&  \begin{bmatrix} 0.2 \\ 0.1 \end{bmatrix} \end{array} \right. \end{eqnarray} $$

と定義します。

また、入出力に対する雑音wとvの分散を

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{w}_t \sim N \left( 0,0.2^2 \right) \\ \boldsymbol{v}_t \sim N \left( 0,0.3^2 \right) \end{array} \right. \end{eqnarray} $$

と定義し、そして各々の共分散QとRを

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{Q} &=&  \begin{bmatrix} 0.2^2 & 0 \\ 0 & 0.2^2 \end{bmatrix} \\ \boldsymbol{R} &=&  \begin{bmatrix} 0.3^2 & 0 \\ 0 & 0.3^2 \end{bmatrix} \end{array} \right. \end{eqnarray} $$

と定義します。

ロボットの位置情報（X軸とY軸）について、目標となる軌跡をxDes、雑音による影響を受けた実際の軌跡をxAct、そしてカルマンフィルタにより推定された軌跡をxEstと定義します。

ロボットの初期位置は[0,0]なので、これら３つの位置情報は[0,0]で初期化します。

さらに、推定値xEstの確からしさを示す誤差共分散Pについて、時刻t=0での推定値[0,0]は確かなので、誤差共分散Pを単位行列Iで初期化します

これらの初期設定をMATLABで記すと以下のようになります。

F = eye(2); % State Matrix
H = eye(2); % Output Matrix

u = [0.2;0.1]; % Input Signal Vector

w = [0.04;0.04]; % Input Gaussian noise
v = [0.09;0.09]; % Output Gaussian noise
Q = diag(w); % Covariance Matrix
R = diag(v); % Covariance Matrix

xDes = [0;0]; % Desired Trajectory
xAct = [0;0]; % Actual Trajcectory
xEst = [0;0]; % Estimated Trajectory

P = eye(2); % Initialize Covariance Matrix

予測ステップ

この予測ステップでは、1つ前の時刻t-1で推定したロボットの位置xEstと入力信号u_tを基に、時刻tでのロボットの位置xEstを推定します。

この時、状態方程式に含まれる入力に対する雑音wの影響は考慮しません。

その代わりに、共分散Qを用いて、推定した位置xEstの確からしさを示す誤差共分散Pを予測します。

この予測ステップで用いる状態方程式と誤差共分散の式を表すと

$$ \begin{eqnarray} \left\{ \begin{array} \hat{\boldsymbol{x}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{x}}_{t-1|t-1} + \boldsymbol{B}_t \boldsymbol{u}_t \\ \hat{\boldsymbol{P}}_{t|t-1} = \boldsymbol{F}_t \hat{\boldsymbol{P}}_{t-1|t-1} {\boldsymbol{F}_t}^T + \boldsymbol{Q}_t \end{array} \right. \end{eqnarray} $$

のようになります。

これら予測ステップでの計算をMATLABで記すと以下のようになります。

xEst = F*xEst + u; % Predicted State Estimate
P = F*P*F' + Q; % Predicted Error Covariance

更新ステップ

この更新ステップでは、実際の観測値zと予測（推定）した位置xEstで得られるはずの観測値との差を求め、カルマンゲインを求めます。

そして、求めたカルマンゲインを用いてロボットの推定位置xEstと誤差共分散Pを更新します。

移動ロボットが予測ステップで推定した位置xEstに存在すると考えた時に、得られるはずの観測値は出力方程式より

$$ \hat{\boldsymbol{z}} =  \boldsymbol{H}_t \boldsymbol{xEst} $$

と求めることが出来ます。

先程の予測ステップの場合と同様に、この時に出力方程式に含まれる雑音vによる影響は考慮をしません。

その代わり、観測値の確からしさを示す誤差共分散Rを、推定した位置xEstの確からしさを示す誤差共分散Pと共に用いて、カルマンゲインKを算出します。

そして、求めたカルマンゲインKと観測値yを基にして、ロボットの推定位置xEstと誤差共分散Pを更新します。

この更新ステップで行う計算式を表すと

$$ \begin{eqnarray} \left\{ \begin{array} \tilde{\boldsymbol{y}}_t = \boldsymbol{z}_t – \boldsymbol{H}_t \hat{\boldsymbol{x}}_{t|t-1} \\ \boldsymbol{S}_t = \boldsymbol{R}_t + \boldsymbol{H}_t \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T \\ \boldsymbol{K}_t = \boldsymbol{P}_{t|t-1} {\boldsymbol{H}_t}^T {\boldsymbol{S}_t}^{-1} \\ \hat{\boldsymbol{x}}_{t|t} = \hat{\boldsymbol{x}}_{t|t-1} + \boldsymbol{K}_t \tilde{\boldsymbol{y}}_t \\ \hat{\boldsymbol{P}}_{t|t} = \left( \boldsymbol{I} – \boldsymbol{K}_t \boldsymbol{H}_t \right) \boldsymbol{P}_{t|t-1} \end{array} \right. \end{eqnarray} $$

となります。

また、更新ステップでの計算をMATLABで記すと以下のようになります。

y = z - H*xEst; % Innovation or Measurement Pre-fit Residual
S = R + H*P*H'; % Innovation or Pre-fit Residual Covariance
    
K = P*H'/S; % Optimal Kalman Gain
    
xEst = xEst + K*y; % Updated State Estimate
P = (eye(2) - K*H)*P; % Updated Estimate Corvariance

シミュレーション結果

紹介した予測ステップと更新ステップを順に繰り返すことで、カルマンフィルタを用いた移動ロボットの自己位置推定を実現することが出来ます。

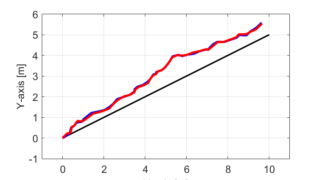
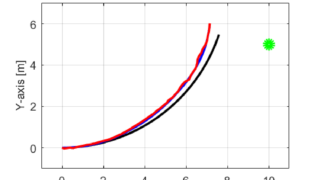
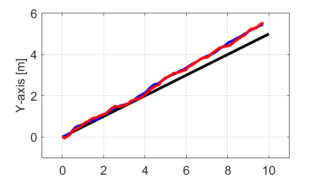
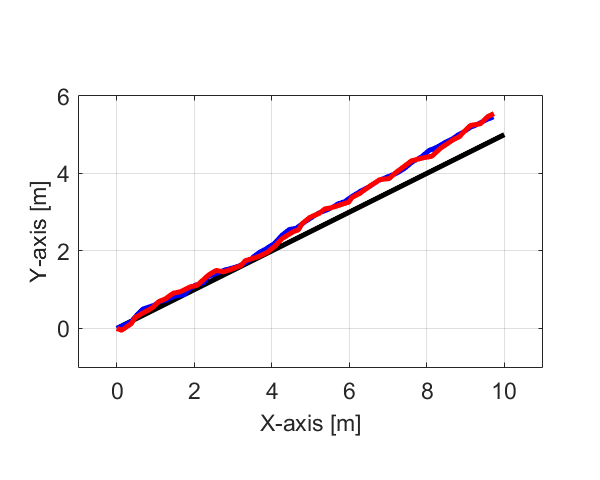
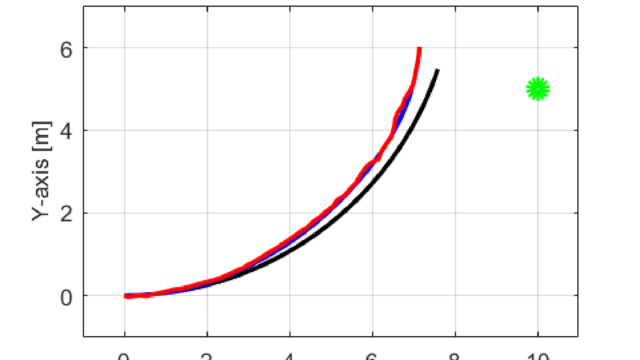
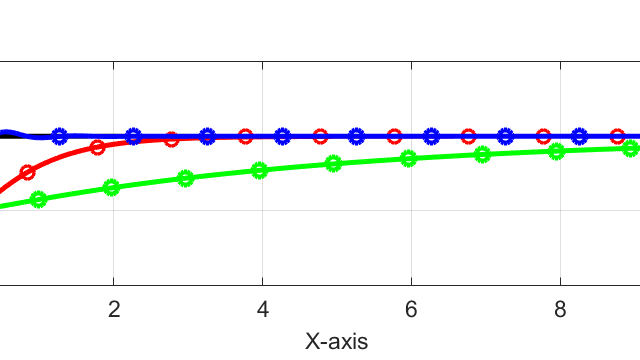
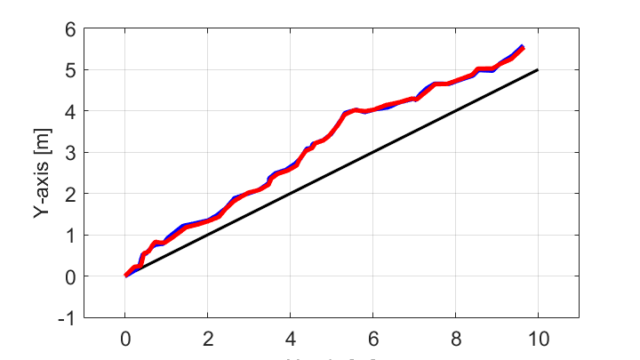
今回紹介したアルゴリズムを実際に用いてシミュレーションを行った結果をX-Y平面のグラフに示します。

シミュレーション結果からも分かるように、目標軌跡（黒線）から実際のロボットの軌跡（青線）がずれた場合でも、カルマンフィルタを用いた自己位置推定によりロボットの現在位置が推定（赤線）できています。

まとめ

今回は、カルマンフィルタを用いた移動ロボットの自己位置推定のアルゴリズムを実装し、実際にシミュレーションを用いて動作の確認を行いました。

今回までに紹介した方法を用いることで、線形動的システムで表される移動ロボットの位置をカルマンフィルタを用いて推定することが出来ます。

次回は、ロボットや自動運転車などの対象のシステムが非線形の場合について、拡張カルマンフィルタを用いた自己位置推定の方法を紹介していきたいと思います。

拡張カルマンフィルタって何？：カルマンフィルタでロボットの位置推定をしてみよう（５） 今回のシリーズでは、自動運転車や移動ロボットを制御するためにとても重要な正確な位置を知る方法として、カルマンフィルタを用いたロボ...

合わせて読みたい

実際にシミュレーションに用いたMATLABコードを紹介しています。

カルマンフィルタでロボットの自己位置推定をするプログラムの紹介 このシリーズでは、ロボットや自動運転車を制御する際に重要な、ロボットや車の正確な位置を得る方法として、カルマンフィルタを用いたロ...