本シリーズでは、車やロボットの自動運転を実際に行うために必要となる制御工学の情報を紹介していきます。
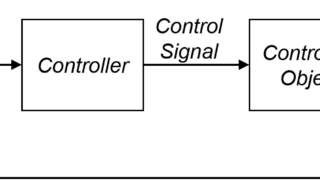
以前の記事では、X軸上にある目標軌跡について、車と目標軌跡との誤差から自動運転車を制御する方法を紹介しました。
今回の記事では、シミュレーションの際に使用したプログラム（MATLAB）について説明したいと思います。
今回の記事で取り扱う問題
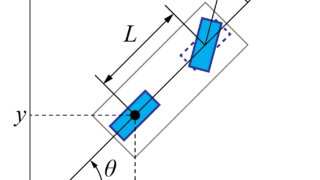
以前の記事でも紹介した通り、複雑な自動運転車を制御する前段階として問題をシンプル化し、目標の軌跡がX軸上のみに存在する場合を考えます。
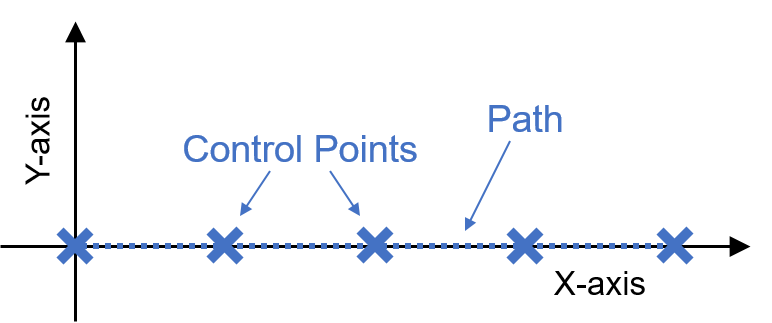
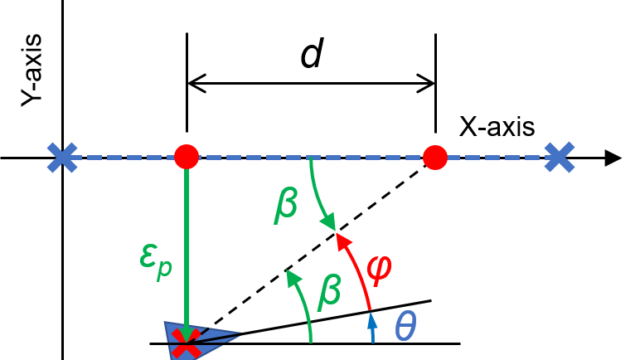
このように与えられた目標軌跡を追従する車の自動制御を行うために、車の現在位置と目標軌跡との誤差を算出します。
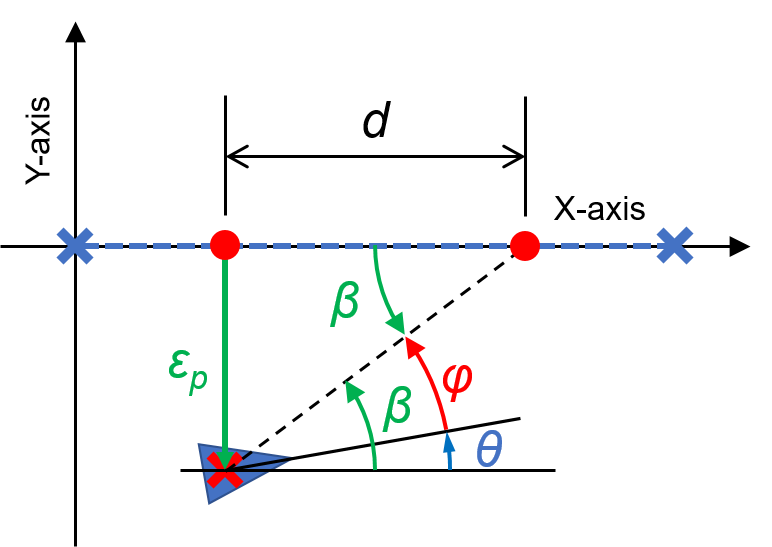
そして、この誤差\(\varepsilon_p\)を用いて、車のハンドル角度\(\phi\)を求めていきます。
最後に、求めたハンドル角度を車に与えることで、目標軌跡に追従するように車を制御することが出来ます。
詳しい説明については、こちらの記事を参考にしてください。
使用したプログラム
今回の記事で取り扱っている自動運転車の問題について、以下のMATALABのプログラム（コード）を用いてシミュレーションを行いました。
Ts = 0.01; % Sampling Time Tt = 20; % Simulation Time L = 0.2; % Distance between Front and Rear Wheels v = 1; % Velocity K = 3; % Parameter of Steering % Desired Path R = [ 0,0; 20,0; ]; % Initial Car Conditions P.x = 0; P.y = 1; P.th = deg2rad(0); Results = P; for i = Ts:Ts:Tt % Calculate Error Err = P.y; % Calculate Steering Angle Beta = atan2(Err,-K); Phi = Beta - P.th; % Calculate Velocity and Angular Vel. dx = v*cos(P.th); dy = v*sin(P.th); dth = v/L*tan(Phi); % Update Current Conditions P.x = dx*Ts + P.x; P.y = dy*Ts + P.y; P.th = dth*Ts + P.th; Results = [Results,P]; end
初期条件
シミュレーションに必要となる初期条件を以下のように設定します。
Ts = 0.01; % Sampling Time Tt = 20; % Simulation Time L = 0.2; % Distance between Front and Rear Wheels v = 1; % Velocity K = 3; % Parameter of Steering % Desired Path R = [ 0,0; 20,0; ]; % Initial Car Conditions P.x = 0; P.y = 1; P.th = deg2rad(0);
今回のシミュレーションでは、
- シミュレーション時間とサンプリング時間
- 車の前後輪距離、速度
- ハンドル角度算出用パラメータ
- 目標軌跡
- 車の初期状態（位置と向き）
を初期条件として設定しました。
誤差算出
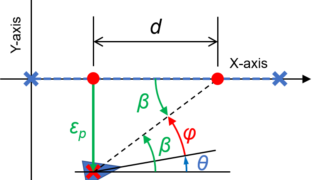
目標軌跡（今回はX軸）と現在の車の状態との誤差を算出します。
% Calculate Error
Err = P.y;
今回のシミュレーション条件では、目標軌跡と車との誤差は、車のY軸の状態値になります。
ステアリング角度
算出した誤差を基に、ハンドルの角度φを算出します。
% Calculate Steering Angle
Beta = atan2(Err,-K);
Phi = Beta - P.th;
まず、目標軌跡との誤差εとパラメータdから角度βを求めます。
そして、その角度βと現在の車の向きθより、ステアリング（ハンドル）角度φを算出します。
状態の速度算出
算出したステアリング角度φと初期条件で設定した速度vを基に、状態xの速度を求めます。
% Calculate Velocity and Angular Vel.
dx = v*cos(P.th);
dy = v*sin(P.th);
dth = v/L*tan(Phi);
算出に用いた式についての詳細は、こちらの記事を参考にしてください。
状態を更新
最後に、算出した状態の速度（角速度）とサンプリング時間Tsを基に、状態xを更新します。
% Update Current Conditions
P.x = dx*Ts + P.x;
P.y = dy*Ts + P.y;
P.th = dth*Ts + P.th;
現在の状態に、速度にサンプリング時間をかけた値を加えて求めます。
まとめ
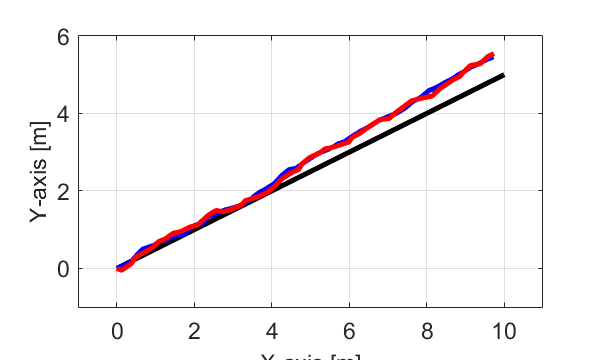
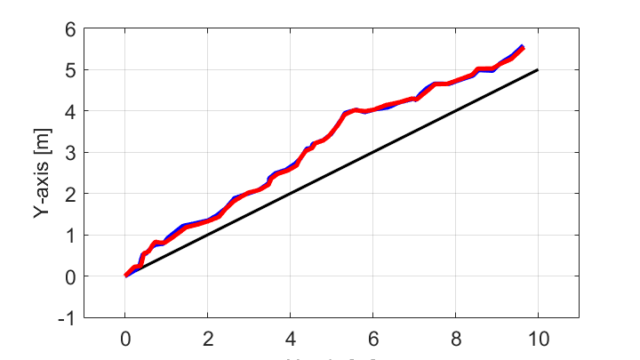
今回の記事では、以前紹介したX軸上に存在する目標軌跡に対する自動運転車の制御について、シミュレーションに用いたプログラムを紹介しました。
今回はMATLABを用いましたが、基本的な考え方はどのプログラム言語でも同じなので、好きな言語に置き換えても大丈夫です。
問題がシンプルなのでプログラムと言えるレベルかは分かりませんが、何かの参考になれば幸いです。
ELEGOO Arduinoスターターキット
UNO R3スマートロボットカー
Raspberry Pi 3 Model b+
