カルマンフィルタでロボットの位置推定をしてみよう！

ロボットや自動運転車を制御するときに、ロボットや車の正確な位置を知ることはとても重要です。

しかし、ロボットを制御するための信号や外部の情報を得るセンサの信号にはノイズが含まれているため、正確な現在位置を得るための情報を得ることが難しくなります。

そこで、不正確な情報の中でもロボットの位置を正確に推定するために、カルマンフィルタ（Kalman　Filter）という手法を用います。

今回からのシリーズでは、このカルマンフィルタを用いたロボットの位置推定の方法を紹介していきたいと思います。

Contents

カルマンフィルタを用いた位置推定
- 位置推定の必要性
- カルマンフィルタによる位置推定
取り扱う線形動的システム
- 状態空間モデル
- 雑音を含んだ状態空間モデル
まとめ

カルマンフィルタを用いた位置推定

今回のシリーズで取り扱うカルマンフィルタによるロボットの位置推定問題を説明します。

位置推定の必要性

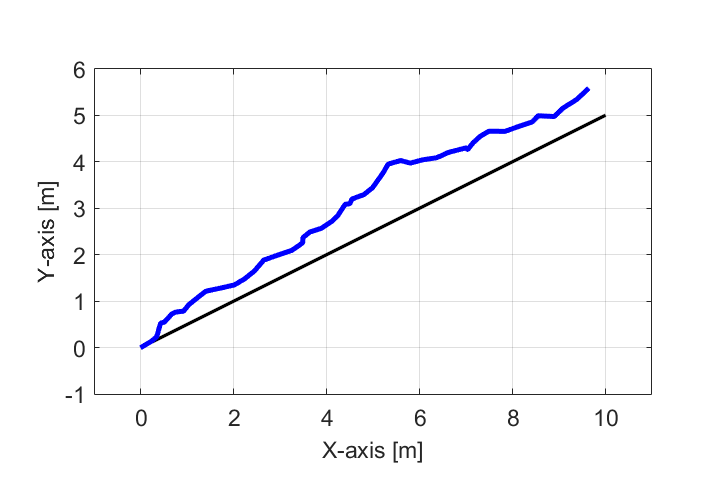
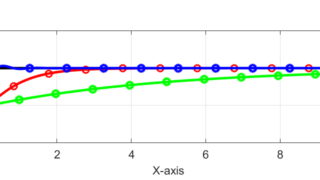
ロボットは図のように黒線で表される目標軌跡に沿って、点[0,0]から点[10,5]に向かって直進するように指示を受けています。

しかし、入力信号に対するノイズの影響により、実際のロボットの移動軌跡は青線のように目標軌跡（黒線）からズレが生じます。

そこで、センサ（GPSなど）を用いてロボットの実際の位置を測定することでロボットの現在位置情報を修正します。

このセンサでの観測値が正確であれば、ロボットの現在位置を正確に把握することが出来ます。

カルマンフィルタによる位置推定

ただ、残念ながらセンサの信号自体にも雑音（ノイズ、誤差）が含まれているため、完全に正確なロボットの位置を得ることはできません。

この様に、ロボットへの入力信号やセンサでの測定データにノイズが入っている場合について、カルマンフィルタを用いて雑音を加味した上でのロボットの自己位置推定を行います。

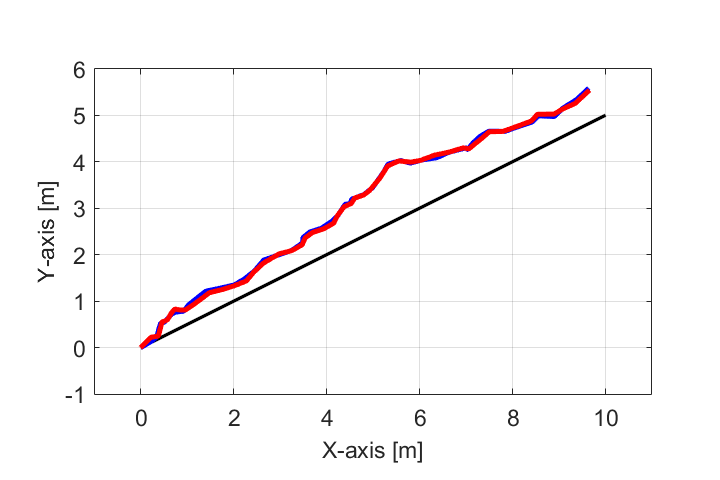
今回のシリーズでは、上の図で表されるように目標軌跡（黒線）から実際の軌跡（青線）がずれた場合についても、赤線のようにロボットの現在位置が推定できるようカルマンフィルタを用いた自己位置推定の方法を紹介していきます。

取り扱う線形動的システム

今回のシリーズでは、カルマンフィルタを用いて位置推定する対象として線形動的システムを取り扱います。

状態空間モデル

まず、取り扱う線形動的システムを状態空間モデルで表します。

時刻tでのロボットの状態ベクトルをx_t、入力ベクトルをu_tとします。

ここで、状態ベクトルx_tには各軸（X軸とY軸）の位置情報

$$ \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$

が含まれており、入力ベクトルu_tには各軸についての移動距離

$$ \boldsymbol{u} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} $$

が含まれています。

また、時刻tでのロボットの観測ベクトルをz_tと表します。

この観測ベクトルz_tは、センサを用いて得たロボットの位置情報

$$ \boldsymbol{z} = \begin{bmatrix} z_1 \\ z_2 \end{bmatrix} $$

で構成されています。

このシステムの状態空間モデルは

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{x}_t = \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t \\ \boldsymbol{z}_t = \boldsymbol{H}_t \boldsymbol{x}_{t} \end{array} \right. \end{eqnarray} $$

と状態方程式と出力方程式を用いて表すことが出来ます。

雑音を含んだ状態空間モデル

ただ、実際にはロボットの入力信号や観測値には雑音（誤差）が生じるため、

$$ \begin{eqnarray} \left\{ \begin{array}{l} \boldsymbol{x}_t = \boldsymbol{F}_t \boldsymbol{x}_{t-1} + \boldsymbol{B}_t \boldsymbol{u}_t + \boldsymbol{w}_t \\ \boldsymbol{z}_t = \boldsymbol{H}_t \boldsymbol{x}_{t} + \boldsymbol{v}_t \end{array} \right. \end{eqnarray} $$

と雑音としてwやvを用いた状態空間モデルで表します。

ここで、入力信号に対する雑音w_tは共分散行列Q_tという入力に対する不確かさを表した行列を用いて

$$ \boldsymbol{w}_t \sim N \left( 0,\boldsymbol{Q}_t \right) $$

と求められます。

また、センサに対する雑音v_tは共分散行列R_tという観測に対する不確かさを示した行列を用いて

$$ \boldsymbol{v}_t \sim N \left( 0,\boldsymbol{R}_t \right) $$

と求めることが出来ます。