今回の記事では、
- ロボットや機械を目的地まで最短距離で動かす経路を見つけたい
- 与えられたマップから、最適なルートを見つけたい
という場合に有用な経路探索の手法としてA*(A-star、エースター)アルゴリズムを紹介します。
経路探索についての基本知識は、こちらの記事を参考にしてください。
A*(A-star)とは
A*探索アルゴリズム(A* Search Algorithm、A*)とはグラフ探索アルゴリズムの内の1つです。
A*アルゴリズムは与えられたスタートから、どこかに存在するゴールまでの最適なルートを探索します。
この最適なルートを探索する際に、A*アルゴリズムではコスト関数f(n)を用いて探索を行います。
ここで、f(n)とはn地点でのコストを示しています。
ここで言うコストというのは、最短な経路を探索する問題では、このコストは距離になります。
また、最短時間を求める問題では、このコストは時間になります。
最適な経路が見つかった場合、この最適経路上にある各n地点でのコストf(n)も最適化されています。
そこで、各地点でのコストを最適化しながら経路を探索することで、最適な経路を見つけます。
A*では、この最適な(最短な)経路を探索するために必要なn地点でのコストf(n)を
$$ f(n) = g(n) + h(n) $$
という式で算出します。
ここでg(n)とは、スタートからn地点までのコスト(距離や時間)です。
そしてh(n)とは、n地点からゴールまでの予想されるコスト(距離や時間)です。
A*アルゴリズムではスタートからのコストg(n)に加えて、ゴールまでの予想コストh(n)を考慮して経路探索を行います。
ここで重要なことは、ゴールまでのコストは予想値だということです。
そもそも、ゴールまでのコストが分かっているということは、ゴールまでの経路が分かっているということなので、経路探索する必要がないですからね。
では、どのようにこの予想値を算出するのか、またどう使用するのかを説明していきます。
アルゴリズムの流れ
今回の記事で紹介しているA*アルゴリズムの流れを下図を用いて説明していきます。
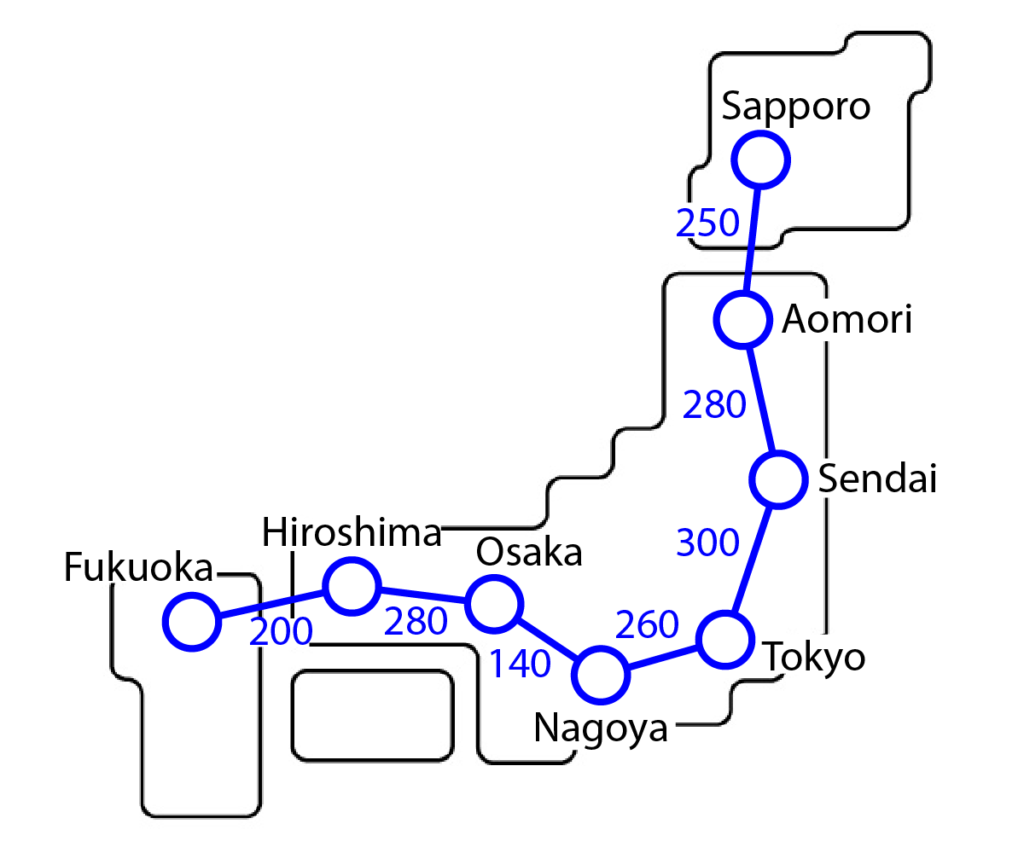
上のようなグラフで与えられたマップについて、東京をスタートとしてゴールの札幌までの最短な経路をA*探索アルゴリズムを用いて求めていきます。
予測コストを考えない場合
スタート地点の東京から北(上方向)と西(左方向)に道が伸びています。
この2つの選択肢の内、コストf(n)が低い方を選んで経路を探していきます。
それぞれの方向に進んだ場合の次の町(点、〇)までのコストは、北の仙台には300km、西の名古屋へは260kmです。
もし、コストf(n)を求める際にスタートからの距離のみを考慮した場合は、距離の近い西の町(名古屋)を選択することになります。
取り扱っている地図を見て頂けると分かるように、明らかに札幌に行くための最適な経路は北の仙台に行った方が良いです。
しかし、探索する際にスタートからのコストのみを考慮すると、西側に伸びる名古屋方向への道を探索してしまいます。
これにより、探索に必要な時間が増えてしまいます。
この無駄な探索を減らすために、A*アルゴリズムでは予測コストも用いて探索を行います。
予測コストの算出方法(例)
A*探索アルゴリズムでは、コストを算出する際にスタートからのコストのみではなく、同時にゴールまでの予想コストを考慮して経路を探索します。
今回はゴールまでの経路は分かっていないが、大体の位置が分かっている場合を考えます。
現実の世界でも、ゴールまでの道筋は分からないけどコッチの方向にどれくらいの距離にあるということは分かっている場合は多いと思います。
今回の例だと、スタート地点の東京から北に約800kmの位置にゴールの札幌があると分かっているとします。
この場合、北の町(仙台)に進んだ場合のゴール(札幌)までの予測コストh(n)を直線距離で予測すると500kmになります。
同様に、西の町(名古屋)に進んだ場合のゴール(札幌)までの予測コストh(n)を直線距離で予測すると950kmになります。
よって、それぞれの町に対するコストは
$$ \begin{eqnarray} f(\mathrm{Sendai}) &=& 300 + 500 = 800 \\ f(\mathrm{Nagoya}) &=& 260 + 950 = 1210 \end{eqnarray} $$
となるため、仙台(北の町)を選択することになります。
ここで、予測値h(n)を算出する際に注意してほしい点があります。
A*探索アルゴリズムは、予測コストh(n)が0以上かつ実際の値以下の場合に、ゴールまでの最短経路が求まります。
言い換えると、A*探索アルゴリズムで最短経路を見つけるためには、予測コストh(n)は必ず実際の値よりも小さくする必要があるということです。
今回の記事で用いた例では、予測コストは現地点とゴールまでの直線距離を基に算出しています。
よって、この予測コストは実際の値より大きくなることはなく、予測値は必ず実際の値以下になります。
そのため、A*探索アルゴリズムは最短経路を求めることが出来ます。
A*(A-star)の利点と欠点
最後に紹介しているA*探索アルゴリズムの利点と欠点を紹介します。
A*探索アルゴリズムの利点
A*探索アルゴリズムを用いることで、最適な解が存在する場合は見つけることが出来ます。
たとえ問題(グラフ)が複雑であったとしても、最適解の探索が可能です。
例えば、今回は高速道路のような一本道のみでしたが、移動手段としては他にも新幹線や飛行機などの選択肢が無数にあります。
そのような複雑な経路探索問題が与えられたとしても、A*アルゴリズムを用いることで最適解を探索で見つけることが出来ます。
さらに、他の方法との比較しても探索に要するノード数が少ないため、必要な計算量が少なく済みます。
A*探索アルゴリズムの欠点
欠点としては、解を見つけるためには、グラフのノード数が有限である必要があり、またコストは固定値である必要があります。
今回の例では、都市の位置は移動することはなく、また移動手段にかかるコストも変化がしないため、A*で最適解を見つけることが出来ました。
もし、目的地が場所ではなく、移動している友人だと考えます。
この場合、目的地が移動しているため必要なコストも変動してしまい、解を見つけることはできません。
そして、A*を用いた探索に必要な時間は、どれくらい正確に予測コストを算出できるかにかかっています。
今回は札幌は東京よりも北に800kmの場所にあるという情報をもとに予測コストを算出しました。
この前情報が全く無い場合や、そもそも目的地がどの方向にあるか分からない場合は、正確に予測コストを算出できなくなり、A*を用いた最適な経路の探索に必要な時間が増大します。
まとめ
今回の記事では、経路探索の手法としてA*探索アルゴリズムを紹介しました。
次回は、今回紹介したA*アルゴリズムを用いて実際に経路を探索するプログラムを紹介したいと思います。

























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
