日常的にGoogleマップや乗り換えアプリなどで経路探索を行う方は多いと思います。
これらの技術によって、僕たちは最適な道順を選んだり、目的地に早く着けたりすることが出来ます。
今回からの記事では、この様な経路探索を行うために、グラフ理論を用いた経路探索問題について紹介したいと思います。
グラフ探索問題
グラフ探索問題とは、グラフ理論におけるグラフについて、スタートからゴールまでの経路を探索する問題です。
グラフとは
下のようなグラフが与えられた場合を考えます。
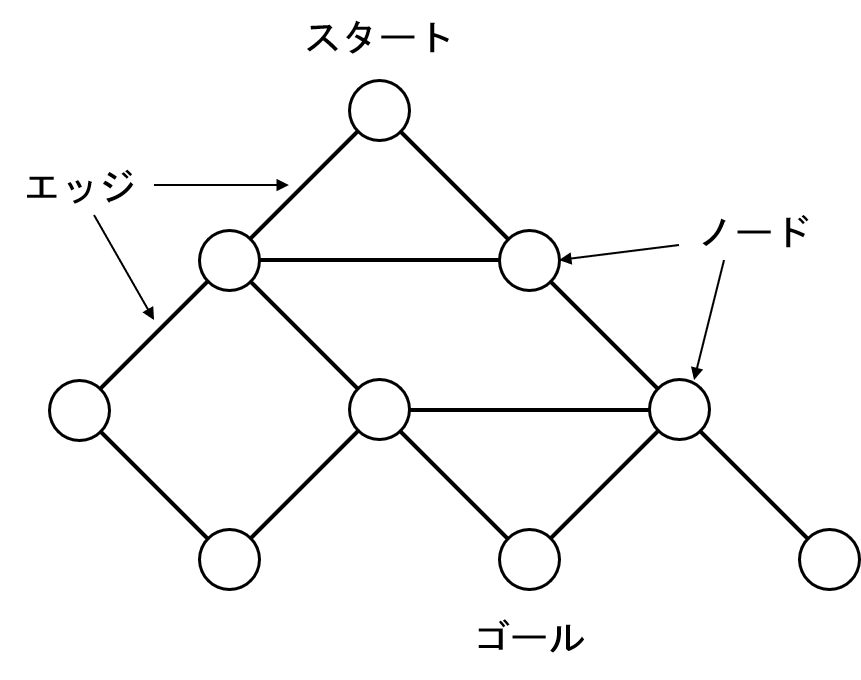
このグラフについて、〇はノード(節点、頂点)と言い、ノード同士を繋いでいる線をエッジ(枝、辺)と言います。
2つのノードがエッジで繋がれていれば、そのノード間を移動可能です。
反対に、2つのノードがエッジで繋がれていない場合は、そのノード間は移動できません。
それぞれのエッジにはコスト(重み)がついており、2つのノード間のエッジを移動する際に与えられます。
地図をグラフで表す
今回の記事では、地図(マップ)をグラフ理論におけるグラフで表した場合を取り扱います。
地図とグラフの関係は下の表の通りです。

グラフに含まれるノードは、地図上における町や駅、ジャンクションにあたります。
そして、エッジはその街や駅をつなぐ道路や線路を表しています。
エッジにつけられたコストとは距離や時間、値段などを表します。
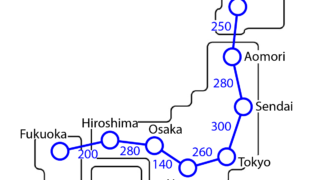
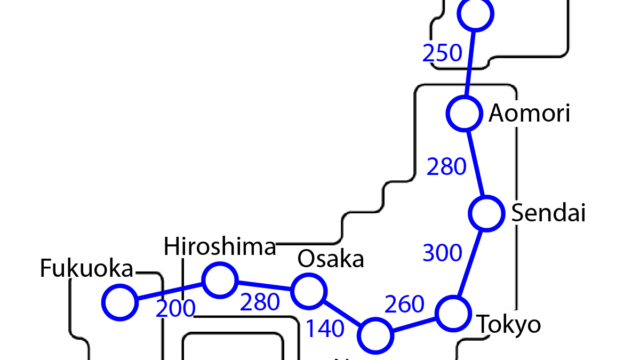
これら基に、それぞれの町を車で移動する場合の移動経路を距離を考慮しながら描いたマップは下のようになります。
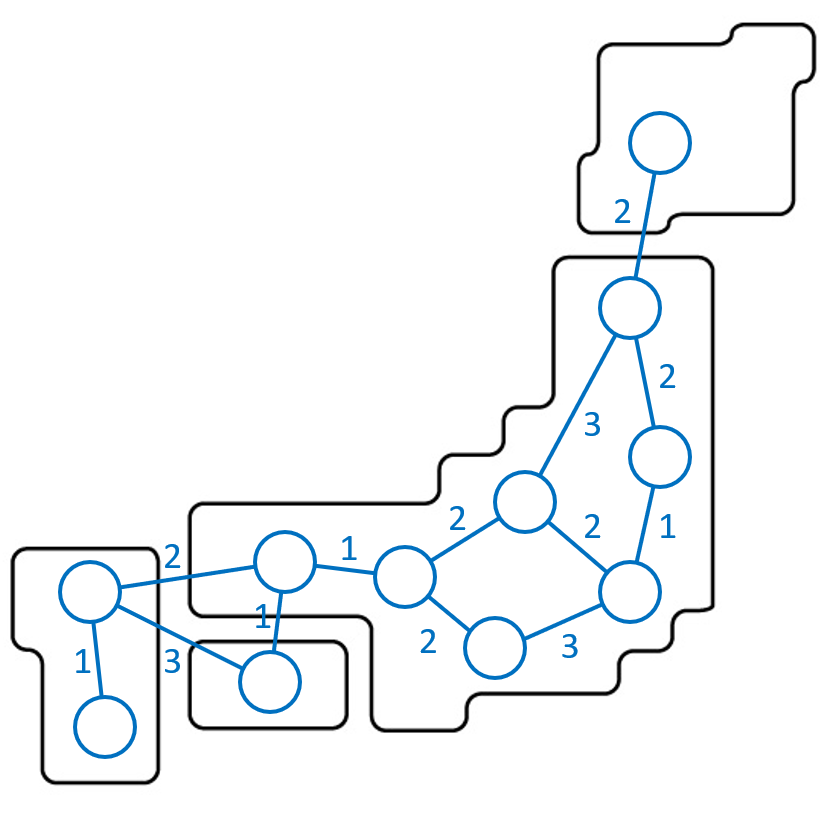
このようなマップについて、経路探索法を用いて経路を解くことで、スタートからゴールまでの経路を見つけます。
経路探索法
与えられたマップについて、スタートからゴールまでの最短な経路を探索する方法には、様々な方法があります。
例えば
- 幅優先探索
- 深さ優先探索
- Dijkstra’s法
- A*アルゴリズム
などがあります。
今後の記事では、これらの経路探索法について紹介しながら、それぞれの利点や欠点を紹介していきたいと思います。
まとめ
今回は、ルート案内や乗り換え案内などで用いられている経路探索を行うために、グラフ理論で扱われているグラフについて説明しました。
また、グラフを用いて経路探索を行うための手法のリストを紹介をしました。
次回からは、今回は名前だけ紹介した経路探索法について、それぞれ紹介していきたいと思います。
合わせて読みたい
A*探索アルゴリズムについて
























 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
