状態フィードバックの状態方程式をブロック線図で表す

システムの制御を行う際に、システムの状態をフィードバックして行う制御方があります。

 

以前の記事で紹介した台車型倒立振子の制御でも、台車や振り子の状態をフィードバックすることで制御を行いました。

台車型倒立振子を安定にフィードバック制御する 今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。 前回までの記事...

 

今回は、この状態フィードバックによる制御の様子を、状態方程式からブロック線図を書くことで確認していきたいと思います。

 

 

状態フィードバックとは

状態フィードバックとは、古典制御で行っていた出力yの代わりに、状態変数Xをフィードバックして行う制御法のことです。

 

この状態制御論を用いることで、s平面上の任意の位置に、システムの固有値λを置くことが出来ます。

 

そして、この状態フィードバックの状態方程式は、

$$ \dot{\boldsymbol{ X }} = \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } \boldsymbol{ u}  $$

という形で表されます。

 

今回は、この状態方程式から実際にブロック線図を求めていきたいと思います。

 

 

状態方程式のブロック線図

では、状態フィードバックの状態方程式

$$ \dot{\boldsymbol{ X }} = \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } \boldsymbol{ u } $$

を表すブロック線図を作っていきます。

 

まず、状態Xは行列Aを通過します。

 

 

この様子をブロック線図で表すと下のようになります。

 

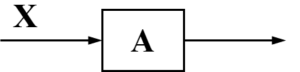
同様に入力uは行列Bを通過しているため、ブロック線図で表すと下のようになります。

 

そして、この２つの信号を足し合わせることで状態Xの時間微分である\(\dot{\boldsymbol{ X }}\)を求めています。

 

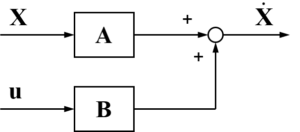
ここで、この状態Xの時間微分\(\dot{\boldsymbol{ X }}\)を積分することで、状態Xを求めることが出来ます。

 

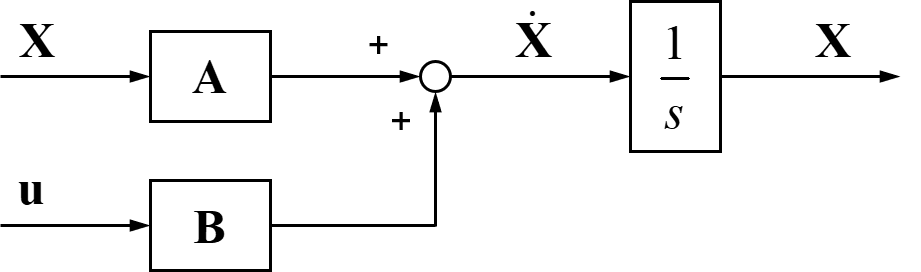
最後に、積分により求めた状態Xを最初に用いた行列Aへの入力に繋げます。

 

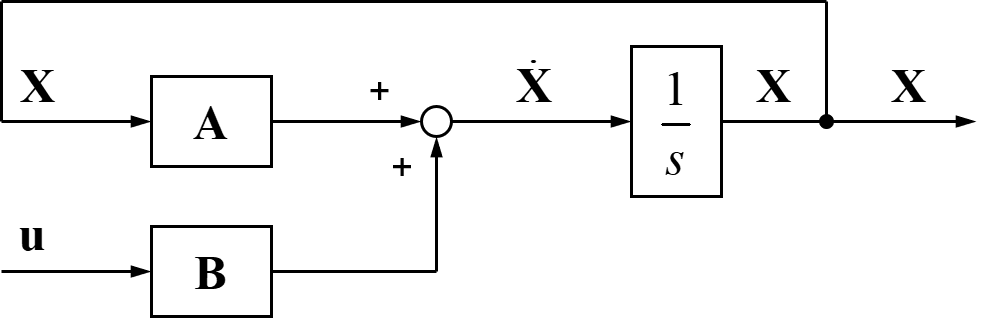
よって求めたブロック線図を整理すると、状態フィードバックの状態方程式

$$ \dot{\boldsymbol{ X }} = \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } \boldsymbol{ u } $$

をブロック線図で表した結果は、

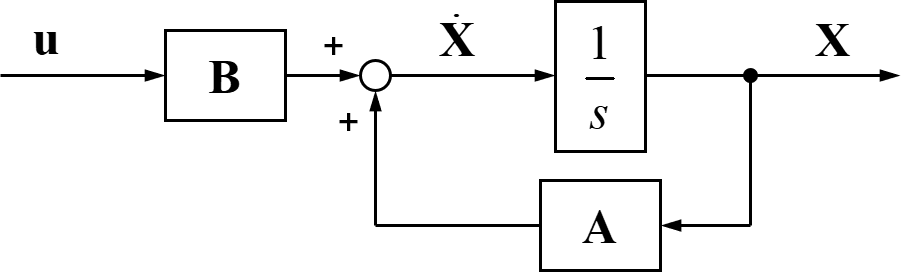
のようになることが分かりました。

 

 

古典制御と状態制御の比較

古典制御で行っている出力yのフィードバックと、今回取り扱っている状態制御での状態Xのフィードバックの様子を示したブロック線図は下の図のようになります。

 

 

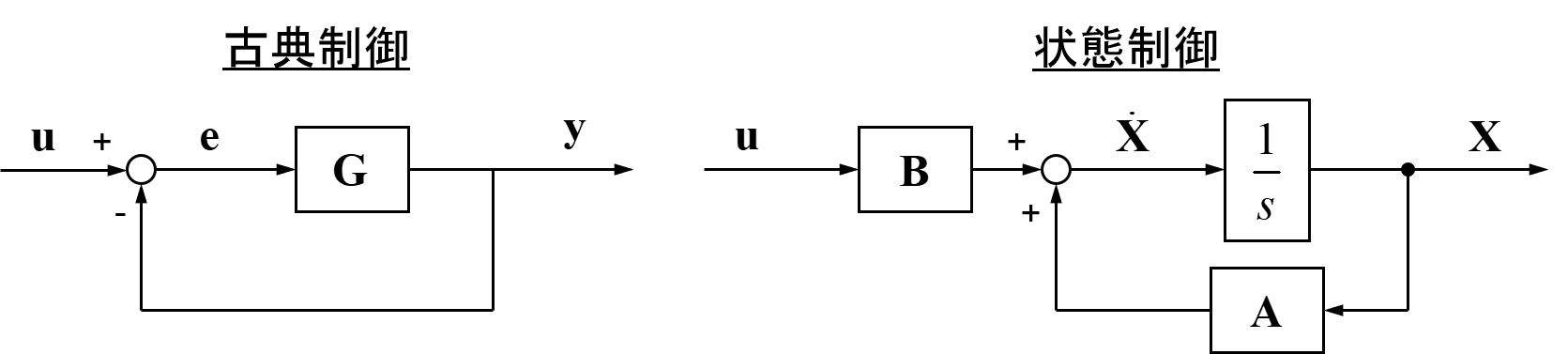
ちなみに、状態制御において入力uを-KXで定義すると、

$$ \begin{eqnarray} \dot{\boldsymbol{ X }} &=& \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } \boldsymbol{ u } \\ &=& \boldsymbol{ A } \boldsymbol{ X } – \boldsymbol{ B } \boldsymbol{ K } \boldsymbol{ X } \\ &=& \left( \boldsymbol{ A } – \boldsymbol{ B } \boldsymbol{ K } \right) \boldsymbol{ X } \end{eqnarray} $$

のような形の状態方程式になります。

 

 

まとめ

今回は、状態フィードバックの様子を理解するために、状態方程式をブロック線図で表す流れを紹介しました。

 

状態方程式と合わせてブロック線図でも確認することで、状態制御論における状態をフィードバックする様子が理解しやすくなるかと思います。