台車型倒立振子を安定にフィードバック制御する

今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。

前回までの記事では、台車型倒立振子を制御するために

• 運動方程式を求めて、
• 状態方程式を求め、
• 状態方程式を線形化し、
• 安定性と可制御性を確認する

までの流れで紹介してきました。

今回は、今まで説明してきた内容をもとに、実際に台車型倒立振子システムの制御の様子をシミュレーション（MATLAB）で行いたいと思います。

取り扱う台車型倒立振子モデル

前回までのおさらいです。

今回のシリーズでは、下図のように表される台車の上に倒立した棒振り子が設置されているモデルを取り扱っています。

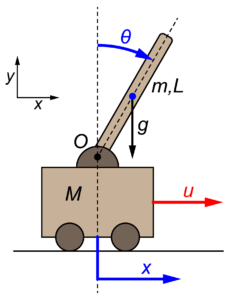
このシステムの状態ベクトルXを

$$ \boldsymbol{ X } = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} x \\ \dot{x} \\ \theta \\ \dot{\theta} \end{bmatrix} $$

としたときの、この台車型倒立振子システムの状態方程式は

$$ \begin{eqnarray} \boldsymbol{ \dot{X} } &=& \begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix} = \begin{bmatrix} f_1(\boldsymbol{X} , u) \\ f_2(\boldsymbol{X} , u) \\ f_3(\boldsymbol{X} , u) \\ f_4(\boldsymbol{X} , u) \end{bmatrix} \\ &=& \begin{bmatrix} x_2 \\ \frac{-\frac{1}{4} m \sin(x_3) \cos(x_3) x_2 x_4 +\frac{1}{6} m L \sin(x_3) {x_4}^2 – \frac{1}{4} m g \sin(x_3) \cos(x_3) + \frac{1}{3} u}{\frac{1}{3} \left( M + m \right) -\frac{1}{4} m \cos^2 (x_3)} \\ x_4 \\ \frac{\frac{1}{4} m L \sin(x_3) \cos(x_3) {x_4}^2 – \frac{1}{2} \left( M + m \right) \sin(x_3) x_2 x_4 – \frac{1}{2} \left( M + m \right) g \sin(x_3) + \frac{1}{2} \cos(x_3) u}{\frac{1}{4} m L \cos^2 (x_3) -\frac{1}{3} \left( M + m \right) L} \end{bmatrix} \end{eqnarray} $$

と非線形関数で表すことが出来ます。

詳しくは、こちらの記事を参考にしてください。

台車型倒立振子を制御するために状態方程式を求める 台車の上に倒立振子が設置されているシステムを台車型倒立振子と言います。 この台車型倒立振子を制御するために、システ...

この非線形な状態方程式を線形化することで、

$$ \begin{eqnarray} \dot{\boldsymbol{ X }} &=& \boldsymbol{ A } \boldsymbol{ X } + \boldsymbol{ B } u \\ &=& \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{3 m g}{ 4 M + m } & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{6 \left( M + m \right) g}{ 4 M L + m L} & 0 \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{4}{4 M + m} \\ 0 \\ – \frac{6}{4 M L + m L} \end{bmatrix} u \end{eqnarray} $$

のように、状態ベクトルXと入力uを含む線形な状態方程式の形で表すことが出来ました。

詳しくは、こちらの記事を参考にしてください。

台車型倒立振子の状態方程式を線形化する 今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。 前回までの記事...

この台車型倒立振子モデル内のパラメータを

$$ \begin{eqnarray} \left\{ \begin{array}{l} M = 10 \ [kg] \\ m = 2 \ [kg] \\ L = 1 \ [m] \\ g = 9.8 \ [m/{sec}^2] \end{array} \right. \end{eqnarray} $$

と定義した時の状態方程式

$$ \dot{\boldsymbol{ X }} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{7}{5} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{84}{5} & 0 \end{bmatrix} \boldsymbol{ X } + \begin{bmatrix} 0 \\ \frac{2}{21} \\ 0 \\ -\frac{1}{7} \end{bmatrix} u $$

から、今回の台車型倒立振子システムは安定性ではないが、可制御性であることが分かりました。

詳しくは、こちらの記事を参考にしてください。

台車型倒立振子の安定性と可制御性を確認する 今回のシリーズでは、台車型倒立振子モデルを取り扱い、システムを安定に制御する方法を紹介しています。 前回の記事では...

今回の記事では、この台車型倒立振子システムについて、制御パラメータを設定して制御を行う方法を紹介していきたいと思います。

制御パラメータの算出

台車型倒立振子を望み通りに制御するために、フィードバック部に含まれる制御パラメータKを算出する方法を紹介します。

はじめに、望み通りの動作になるような固有値λを設定します。

今回の記事では

$$ \boldsymbol{ \lambda } = \begin{bmatrix} -1 \\ -2 \\ -3 \\ -4 \end{bmatrix} $$

のように、固有値λを設定しました。

つぎに、設定した固有値λをもとに、制御パラメータKを算出します。

今回のシステムにおいて、状態フィードバックを求めると

$$ \dot{\boldsymbol{ X }} = \left( \boldsymbol{ A } – \boldsymbol{ B }  \boldsymbol{ K } \right) \boldsymbol{ X } + \boldsymbol{ B } u $$

となります。

状態フィードバックの状態方程式をブロック線図で表す システムの制御を行う際に、システムの状態をフィードバックして行う制御方があります。 以前の記事で紹介した台車型倒立...

そのため、この状態フィードバック内に含まれる行列式

$$ \begin{eqnarray} && \boldsymbol{ A } – \boldsymbol{ B }  \boldsymbol{ K } \\ &=&  \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & – \frac{7}{5} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{84}{5} & 0 \end{bmatrix} – \begin{bmatrix} 0 \\ \frac{2}{21} \\ 0 \\ -\frac{1}{7} \end{bmatrix} \begin{bmatrix} K_1 & K_2 & K_3 & K_4 \end{bmatrix} \\ &=& \begin{bmatrix} 0 & 1 & 0 & 0 \\ -\frac{2}{21} K_1 & -\frac{2}{21} K_2 & – \frac{7}{5} – \frac{2}{21} K_3 & – \frac{2}{21} K_4 \\ 0 & 0 & 0 & 1 \\ \frac{1}{7} K_1 & \frac{1}{7}K_2 & \frac{84}{5} + \frac{1}{7}K_3 & \frac{1}{7}K_4 \end{bmatrix} \end{eqnarray} $$

の固有値が設定した値λになるように、制御パラメータKを設定します。

行列[A–BK]の固有値λを算出するための関係式は

$$ \begin{vmatrix} -\lambda & 1 & 0 & 0 \\ -\frac{2}{21} K_1 & -\frac{2}{21} K_2 -\lambda & – \frac{7}{5} – \frac{2}{21} K_3 & – \frac{2}{21} K_4 \\ 0 & 0 & -\lambda & 1 \\ \frac{1}{7} K_1 & \frac{1}{7}K_2 & \frac{84}{5} + \frac{1}{7}K_3 & \frac{1}{7}K_4 -\lambda \end{vmatrix} = 0 $$

と表されます。

この関係式に含まれる固有値λに選択した値を代入することで、制御パラメータKを求めていきます。

まずλ＝-1のとき、この値を関係式に代入すると

$$ \begin{eqnarray} && \begin{vmatrix} 1 & 1 & 0 & 0 \\ -\frac{2}{21} K_1 & -\frac{2}{21} K_2 + 1 & – \frac{7}{5} – \frac{2}{21} K_3 & – \frac{2}{21} K_4 \\ 0 & 0 & 1 & 1 \\ \frac{1}{7} K_1 & \frac{1}{7}K_2 & \frac{84}{5} + \frac{1}{7}K_3 & \frac{1}{7}K_4 + 1 \end{vmatrix} = 0 \\ &\Rightarrow& -\frac{137}{105} K_1 + \frac{137}{105} K_2 – \frac{1}{7} K_3 + \frac{1}{7} K_4 = \frac{79}{5} \end{eqnarray} $$

のような式が得られます。

同様に、λ＝-2, -3, -4を代入すると

$$ \begin{eqnarray} \lambda = -2 &\Rightarrow& -\frac{107}{105} K_1 + \frac{214}{105} K_2 – \frac{4}{7} K_3 + \frac{8}{7} K_4 = \frac{256}{5} \\ \lambda = -3 &\Rightarrow& -\frac{19}{35} K_1 + \frac{57}{35} K_2 – \frac{9}{7} K_3 + \frac{27}{7} K_4 = \frac{351}{5} \\ \lambda = -4 &\Rightarrow& \frac{13}{105} K_1 – \frac{52}{105} K_2 – \frac{16}{7} K_3 + \frac{64}{7} K_4 = \frac{64}{5} \end{eqnarray} $$

の式が得られます。

これら各固有値λに対する4つの式を連立方程式として

$$ \begin{eqnarray} \left\{ \begin{array}{lllll} -\frac{107}{105} K_1 &+& \frac{137}{105} K_2 &-& \frac{1}{7} K_3 &+& \frac{1}{7} K_4 &=& \frac{79}{5} \\ -\frac{107}{105} K_1 &+& \frac{214}{105} K_2 &-& \frac{4}{7} K_3 &+& \frac{8}{7} K_4 &=& \frac{256}{5} \\ -\frac{19}{35} K_1 &+& \frac{57}{35} K_2 &-& \frac{9}{7} K_3 &+& \frac{27}{7} K_4 &=& \frac{351}{5} \\ \frac{13}{105} K_1 &-& \frac{52}{105} K_2 &-& \frac{16}{7} K_3 &+& \frac{64}{7} K_4 &=& \frac{64}{5} \end{array} \right. \end{eqnarray} $$

とおき、K₁～K₄について解くことで

$$ \begin{eqnarray} \boldsymbol{ K } &=& \begin{bmatrix} K_1 & K_2 & K_3 & K_4 \end{bmatrix} \\ &=& \begin{bmatrix} -17.1429 & -35.7143 & -374.0286 & -93.8095 \end{bmatrix} \end{eqnarray} $$

のように、制御パラメータKを算出することが出来ました。

シミュレーション結果

それでは、求めた制御パラメータKを用いて実際に台車型倒立振子の制御を行っていきます。

今回の記事で紹介するシミュレーションの条件は、振り子が真っすぐ上向きの安定な状態にある初期状態X₀

$$ \boldsymbol{ X_0 } = \begin{bmatrix} x_0 \\ \dot{x}_0 \\ \theta_0 \\ \dot{\theta}_0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} $$

から、5[m]進んで安定した状態X_T

$$ \boldsymbol{ X_T } = \begin{bmatrix} x_T \\ \dot{x}_T \\ \theta_T \\ \dot{\theta}_T \end{bmatrix} = \begin{bmatrix} 5 \\ 0 \\ 0 \\ 0 \end{bmatrix} $$

に移動するような制御の様子をシミュレーションしました。

実際に算出した制御パラメータKを用いて状態X₀からX_Tに移動するようにMATLABでシミュレーションした結果は下の図のようになります。

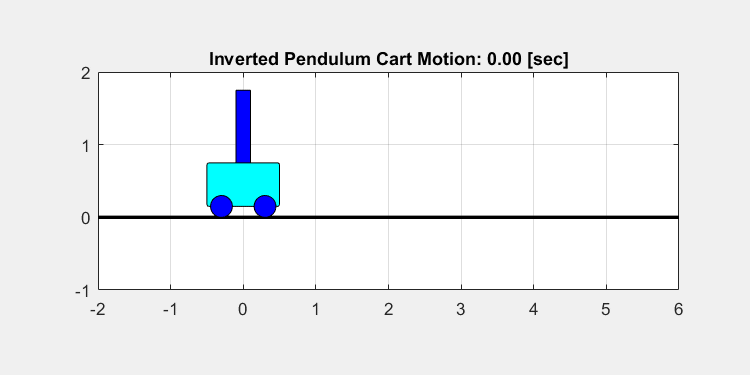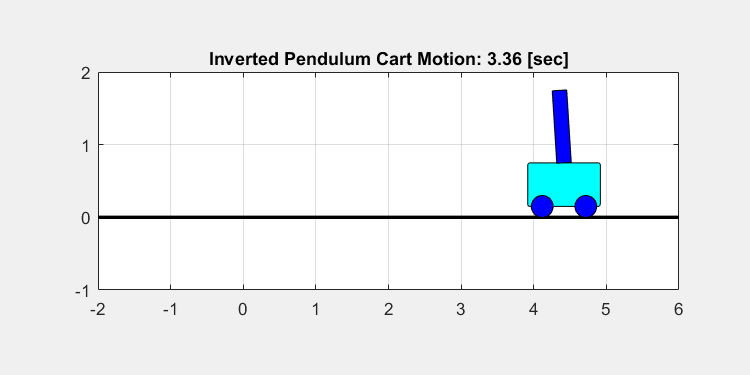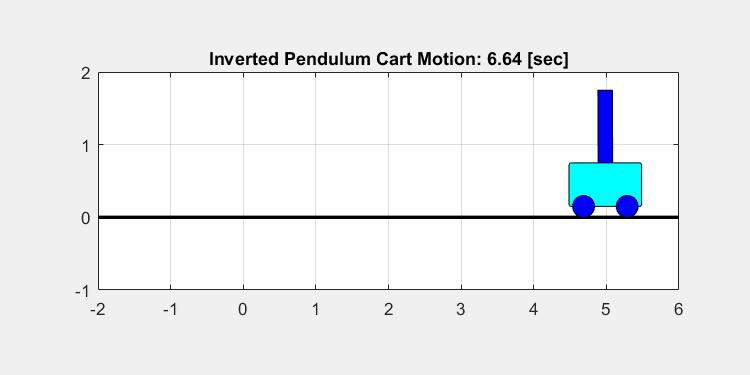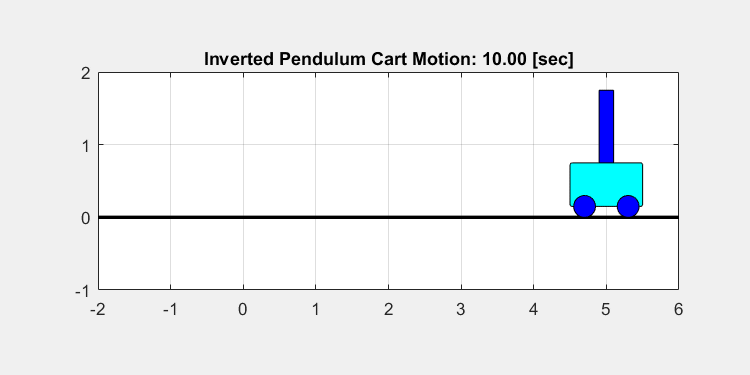
上の動画からも分かるように、最初は位置0にいた台車が、振り子の安定性を保ちながら、位置5に移動していることが分かります。

また、シミュレーション時における各状態のグラフを下のようになります。

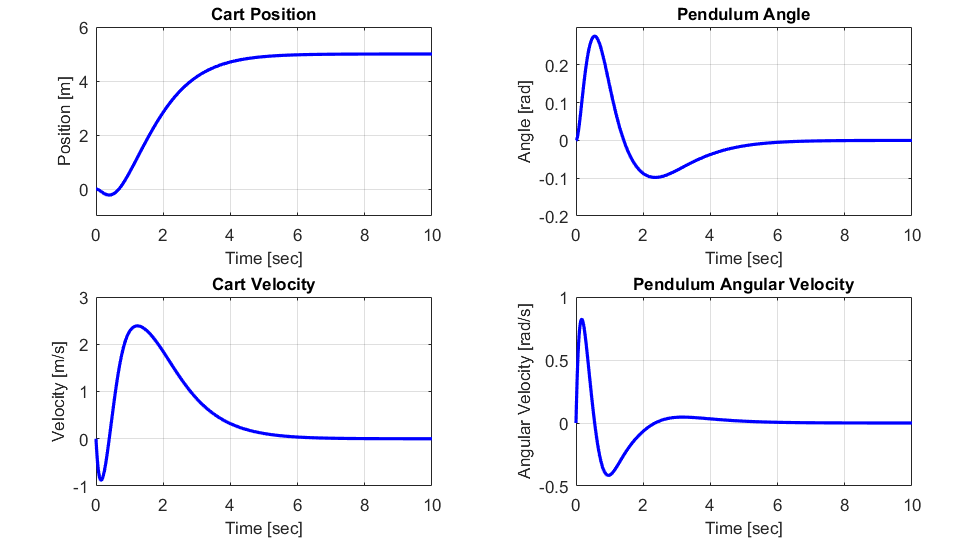
各状態のグラフ（特に左上の台車の位置のグラフ）からも分かるように、台車は最初にマイナス方向（左方向）に少し移動した後に、目標の5mの位置に移動していることが分かります。

この結果から、安定な状態を保っている振り子を乗せた台車を右側に移動させるためには、一度台車を左側に移動させることで振り子を右に少し傾けて安定な状態からズラしたあとに、台車を右に移動させていることが分かります。

まとめ

今回の記事では、台車型倒立振子の制御を行う方法を紹介し、実際にシミュレーションでシステムの動作を確認しました。

台車型倒立振子の制御を行うために、フィードバック回路に含まれる制御パラメータKを算出し、その値を用いることでフィードバック制御を行いました。