根軌跡で制御システムを設計する

根軌跡を用いることで、取り扱いが難しい高い次数の伝達関数を含む複雑なフィードバックシステムの特性を可視化することができます。

今回は、根軌跡についてとその利点、そして根軌跡を描くために必要となる基本的な知識を紹介します。

根軌跡とは

根軌跡とは、システムのパラメータが変化した際の閉ループ伝達関数の極を可視化したものです。

フィードバックシステムの制御は複雑で、必要となる計算量も多く、システムの動作を理解するのが難しいです。

フィードフォワード制御とフィードバック制御でロボットを自由に制御しよう ロボットなどを思い通りに動かすために、フィードフォワード制御とフィードバック制御があります。 この二つの制御方法は...

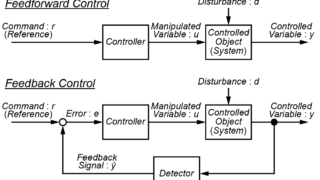
根軌跡を用いることで、定性的にも定量的にも制御システムの情報を得ることが出来ます。

根軌跡のメリット

１次系システムや2次系システムであれば、制御システムの動作を計算を用いて求めることが出来ます。

制御システムがそれ以上の（3次系以上）オーダーとなると、システムの応答を求めることが難しくなります。

このような高い次数のシステムに対して根軌跡を用いることで、目標となるシステム応答を達成するように制御系を設計することが出来ます。

根軌跡のための基礎知識

実際に根軌跡を書くために必要となる基本的な知識を紹介します。

制御システム

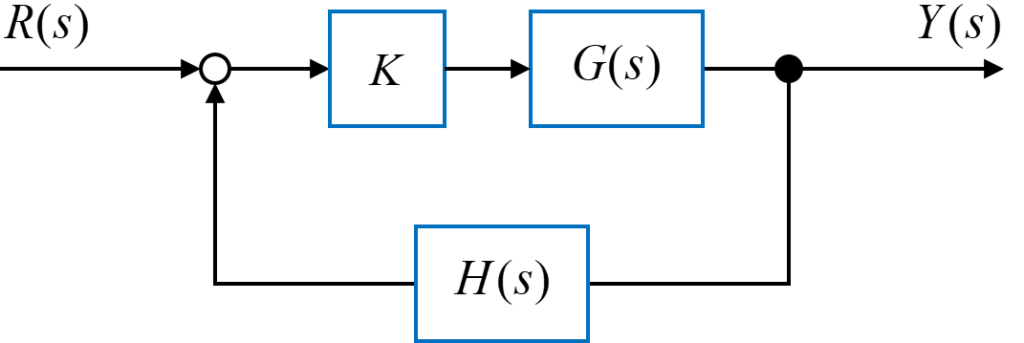
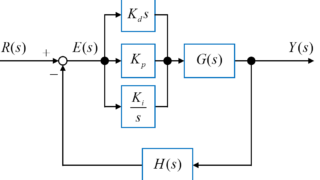
図のようなフィードバックシステム全体の伝達関数\(T(s)\)は、フィードフォワード伝達関数\(G(s)\)とフィードバック伝達関数\(H(s)\)を用いて

$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$

と表すことが出来ます。

ここで、制御対象の伝達関数（フィードフォワード伝達関数）\(G(s)\)の分子と分母を

$$ G(s) = \frac{N_G (s)}{D_G (s)} $$

とし、フィードバック部の伝達関数（フィードバック伝達関数）\(H(s)\)の分子と分母を

$$ H(s) = \frac{N_H (s)}{D_H (s)} $$

とした時、フィードバックシステム全体の伝達関数\(T(s)\)は

$$ T(s) = \frac{K G(s)}{1 + K G(s) H(s)} $$

$$ = \frac{K \frac{N_G (s)}{D_G (s)}}{1 + K \frac{N_G (s)}{D_G (s)} \frac{N_H (s)}{D_H (s)}} $$

$$ \Rightarrow T(s) = \frac{K N_G(s) D_H(s)}{D_G(s) D_H(s) + K N_G(s) N_H(s)} $$

と表すことが出来ます。

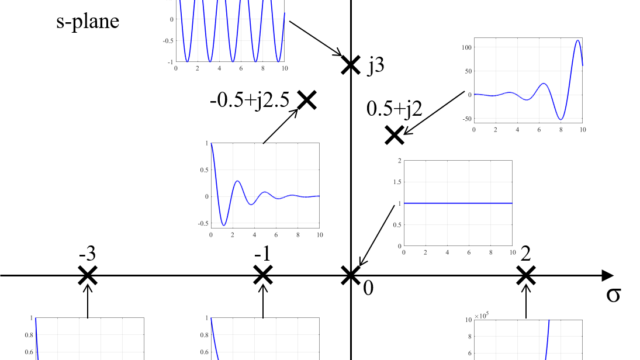
複素数のベクトル表示

複素数を複素平面に表す方法と、その大きさと角度の求め方を紹介します。

複素数が

$$ \sigma + j \omega $$

と与えられた場合を考えます。

この時、複素数内の\(\sigma\)が実数成分で、\(\omega\)が虚数成分を表しています。

この複素数を複素平面上で表すと下の図のようになります。

この複素数の大きさ\(M\)は、実数成分\(\sigma\)と虚数成分\(\omega\)より

$$ M = \sqrt{{\sigma}^2 + {\omega}^2} $$

と求めることが出来ます。

また、この複素数の角度（傾き）\(\theta\)は、実数成分\(\sigma\)と虚数成分\(\omega\)の関係より

$$ \theta = \arctan{\left( \frac{\omega}{\sigma} \right)} $$

と算出することが出来ます。

まとめ

今回は、根軌跡を用いる利点と根軌跡を書くために必要となる基本的な知識として、フィードバック制御システムと複素数のベクトル表示について紹介しました。

次回は、実際に具体的な値を用いて根軌跡を描く方法を紹介していきたいと思います。

フィードバックシステムと伝達関数の極と根軌跡 高い次数の伝達関数を含む複雑なフィードバックシステムの特性を根軌跡によって可視化することが出来ます。 https://ta...