伝達関数の極とインパルス応答

複素平面上での伝達関数の極の位置から、システムのインパルス応答の様子を見ることが出来ます。

今回は、ロボットなどのシステムの伝達関数から求めた極を複素数平面上に示すことで、その

極の位置によるシステムのインパルス応答の様子を紹介します。

伝達関数と極

ロボットなどの動的システムの伝達関数が

$$ G(s) = \frac{b_m s^m+b_{m-1} s^{m-1}+\cdots+b_1 s+b_0}{s^n+a_{n-1} s^{n-1}+\cdots+a_1 s+a_0} $$

と表される場合を考えます。

この伝達関数について、伝達関数の分母

$$ s^n+a_{n-1} s^{n-1}+\cdots+a_1 s+a_0 $$

を特性方程式として解くことで極を求めることが出来ます。

求めた極を用いて、与えられた伝達関数を部分分数展開すると、

$$ G(s) = \frac{k_1}{s – p_1} + \frac{k_2}{s – p_2} +\cdots+ \frac{k_n}{s – p_n} $$

と表すことが出来ます。

ここで、\(p_i\)は伝達関数\(G(s)\)の極を示しています。

このように、互いに独立した極\(p_i\)を用いて、伝達関数を部分分数展開した際の各項をモードと言います。

そして、このような部分分数展開された式をモード展開と言います。

伝達関数の極とインパルス応答

伝達関数\(H(s)\)が周波数領域\(s\)において

$$ H(s) = \frac{k}{s-p} $$

と表されるとき、このシステムのインパルス応答は逆ラプラス変換を用いて時間領域\(t\)に変換することで

$$ h(t) = k e^{pt} $$

と求めることが出来ます。

よって、部分分数展開した伝達関数

$$ G(s) = \frac{k_1}{s – p_1} + \frac{k_2}{s – p_2} +\cdots+ \frac{k_n}{s – p_n} $$

について、逆ラプラス変換を用いてインパルス応答を求めると

$$ g(t) = k_1 e^{p_1 t} + k_2 e^{p_2 t} +\cdots+ k_n e^{p_n t} $$

となることが分かります。

この関係を基に各極とインパルス応答の関係を求めていきます。

極\(p_i\)の実部が正の場合、\(e^{p_i t}\)についてべき数\(p_i t\)が時間経過によってプラス無限大に大きくなるため、このインパルス応答も時間の経過によって無限大に発散します。

反対に極\(p_i\)の実部が負の場合、\(e^{p_i t}\)のべき数\(p_i t\)が時間経過によってマイナス無限大に大きくなるため、そのインパルス応答は時間の経過によってゼロに収束します。

極\(p_i\)に虚部が含まれている（虚部が０でない）場合、そのインパルス応答は振動します。

これは、伝達関数

$$ G(s) = \frac{k}{s – p_1} + \frac{k}{s – p_2} $$

の極\(p_1\)と\(p_2\)が、

$$ p_1 = \sigma + j \omega $$

$$ p_2 = \sigma – j \omega $$

と表されるときに、このインパルス応答は、

$$ g(t) = k e^{p_1 t} + k e^{p_2 t} $$

$$ = k e^{\left(\sigma + j \omega\right) t} + k e^{\left(\sigma – j \omega\right) t} $$

$$ = k e^{\sigma t} e^{j \omega t} + k e^{\sigma t} e^{-j \omega t} $$

$$ = k e^{\sigma t} \left(e^{j \omega t} + e^{-j \omega t}\right) $$

$$ = k e^{\sigma t} \frac{\cos (\omega t)}{2}$$

となるためです。

複素平面上の極とインパルス応答

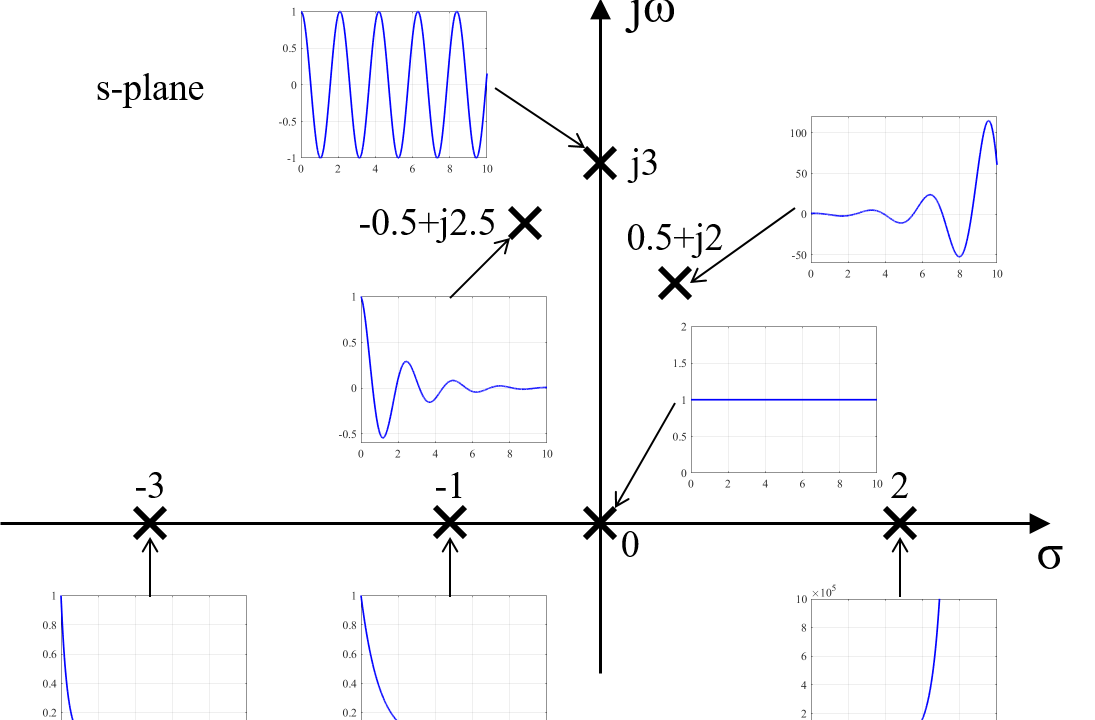
複素平面上（s-palne）に表された極（pole）の位置からインパルス信号を入力された際のシステムの応答（インパルス応答）の様子を予想することが出来ます。

システムの伝達関数の極\(p\)を

$$ p = \sigma + j \omega $$

として、複素平面上（実数軸：\(\sigma\)、虚数軸：\(\omega\)）にプロットします。

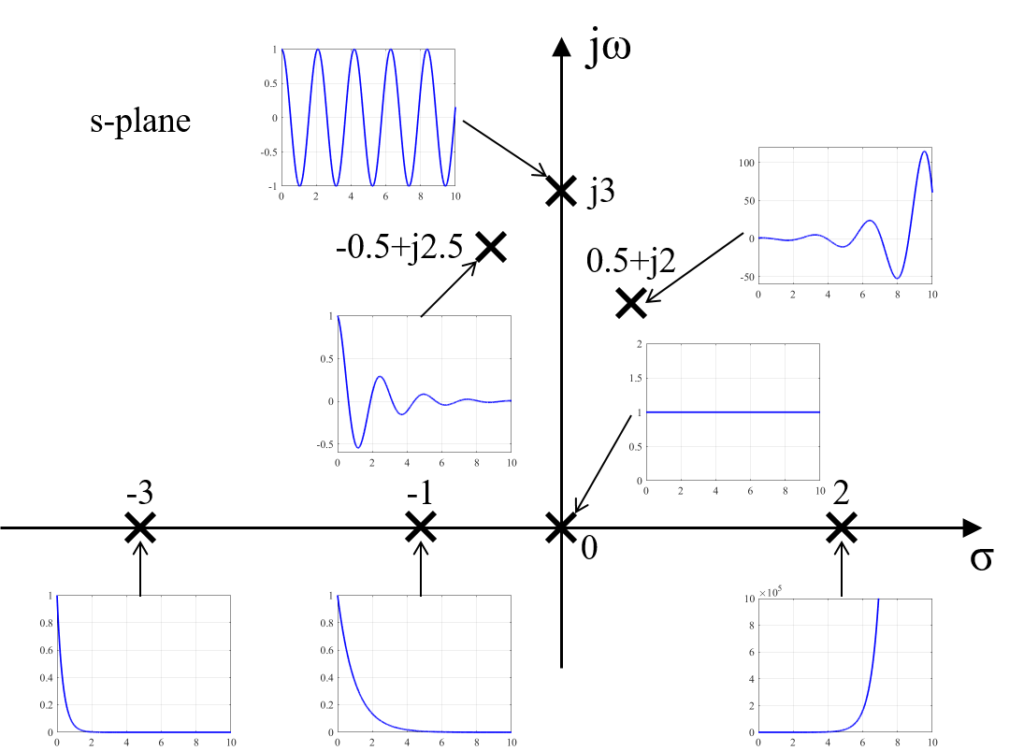
伝達関数の極（\(p = \sigma + j \omega\)）について、虚数軸より右側に極が位置する場合、そのインパルス応答は時間経過とともに発散します。

これは、虚数軸より右側に極が位置するということは、極の実数部\(\sigma\)が正（プラス）となるため、インパルス応答\(e^{p t}\)のべき数\(p t\)が時間経過によってプラス無限大に大きくなるためです。

次に、虚数軸より左側に極が位置する場合、そのインパルス応答は時間経過とともに収束します。

これは、虚数軸より左側に極が位置するということは、極の実数部\(\sigma\)が負（マイナス）となるため、インパルス応答\(e^{p t}\)のべき数\(p t\)が時間経過によってマイナス無限大に大きくなるためです。

極\(p\)が虚数\(\omega\)を含んでいる場合、つまり極が実数軸上にない場合は、そのインパルス応答は振動します。

さらに極が虚数軸上にある場合は、持続振動をします。

このように、複素平面上の極の位置からシステムのインパルス応答を予想することが出来ます。

まとめ

今回は、複素平面上での伝達関数の極の位置とシステムのインパルス応答の様子の関係を紹介しました。