速度比例制御とは、比例器を用いた速度制御系のことです。
速度比例制御系を用いることで、目標速度を追従するように制御することが出来ます。
速度比例制御系については、こちらの記事も参考にしてください。

今回の記事では、速度比例制御系の特徴を伝達関数を用いて紹介したいと思います。
速度比例制御系の伝達関数
本記事で使用する速度比例制御系の伝達関数について、以前の記事の復習をしたいと思います。

上のブロック線図で表される比例器を用いたフィードバック制御による速度比例制御系について、速度指令vrから速度応答vmの閉ループ伝達関数は
$$ G_{vr} = \frac{K_{vp}/m}{s+K_{vp}/m} = \frac{\omega_{vc}}{s+\omega_{vc}} $$
と表されます。
そして、外乱fdから速度応答vmの閉ループ伝達関数は
$$ G_{vd} = \frac{1/m}{s+K_{vp}/m} = \frac{1}{m} \frac{1}{s+\omega_{vc}} $$
と表すことが出来ます。
詳しくは、こちらの記事を参考にしてください。

安定性
まず速度比例制御系システムの安定性について考えていきます。
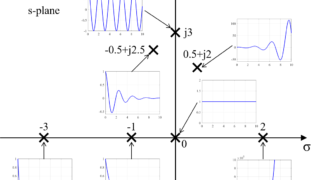
閉ループ伝達関数の極が複素平面の左側にあればシステムは安定であるといえます。
システムの安定性と複素平面の関係については、こちらの記事を参考にしてください。
速度指令vrから速度応答vmの閉ループ伝達関数Gvr
$$ G_{vr} = \frac{K_{vp}/m}{s+K_{vp}/m} = \frac{\omega_{vc}}{s+\omega_{vc}} $$
において、極となる分母について考えます。
まず、制御対象の質量mは正(プラスの値)です。
そのため、速度比例ゲインKvpが正であるとき、Kvp/mも正となります。
その結果、閉ループ伝達関数Gvrの分母に含まれるωvcについて
$$ ω_vc=K_vp/m $$
で表されることから、速度比例ゲインKvpと質量mがともに正であるとき、ωvcも正となる事が分かります。
これより、速度比例ゲインKvpを正の値にすることで、閉ループ伝達関数Gvrの極は複素平面の左側の実軸上に存在するため、このフィードバック系は安定であるといえます。
システムの安定性と複素平面の関係については、こちらの記事を参考にしてください。

指令値応答性
次に、速度比例制御系システムの指令値に対する応答性について考えます。
システムの応答性について、閉ループ伝達関数の極が複素平面の実軸上から離れるほど応答性は高くなるといえます。
つまり、速度指令vrから速度応答vmの閉ループ伝達関数Gvrに含まれるωvcの値が大きくなるほど、システムの応答性は向上します。
この閉ループ伝達関数Gvr内のωvcは、
$$ ω_vc=K_vp/m $$
で求められるため、
- 速度比例ゲインKvpを大きくする
- 質量mを小さくする
ことでωvcの値は大きくなります。
ここで質量mについて、通常は自由に変化できない(制御できない)ことが多いです。
そのため、速度比例ゲインKvpを変えることでシステムの応答性を変化させることが出来ます。
ちなみに、s=0における閉ループ伝達関数Gvr(s)は、
$$ G_{vr} (s=0) = \frac{\omega_{vc}}{s+\omega_{vc}} = \frac{\omega_{vc}}{\omega_{vc}} = 1 $$
となります。
これより、単位ステップ応答に対する速度比例制御系の定常偏差は0であると分かります。
外乱抑制
最後に、速度比例制御系システムの外乱抑制についても考えていきます。
外乱抑制についても、閉ループ伝達関数Gvd内のωvcの値が大きくなるほど外乱抑制効果は大きくなるといえます。
これに加えて、質量mが大きい場合も外乱抑制効果は大きくなります。
単位ステップ外乱に対する定常応答Gvd(s=0)は、
$$ \begin{eqnarray} G_{vd}(s=0) &=& \frac{1}{m} \frac{1}{s+ω_{vc}} \\ &=& \frac{1}{m} \frac{1}{ω_{vc}} \\ &=& \frac{1}{m \left( K_{vp}/m \right)} \\ &=& \frac{1}{K_{vp}} \end{eqnarray} $$
となります。
これより、速度比例ゲインKvpが大きくなるほど、単位ステップの外乱に対する定常応答は小さくなることが分かります。
一方で、この外乱に対する定常応答を無くす(0にする)ためには、速度比例ゲインKvpを無限大(∞)にしなければならないともいえます。
まとめ
今回の記事では、速度比例制御系について、伝達関数を用いながらシステムの特徴を紹介しました。
速度比例制御を用いたフィードバック系の伝達関数から、システムの安定性、指令値に対する応答性、外乱に対する抑制について特徴を説明しました。
次回の記事では、実際にシミュレーションを用いて今回紹介した速度比例制御系の特徴を確認したいと思います。




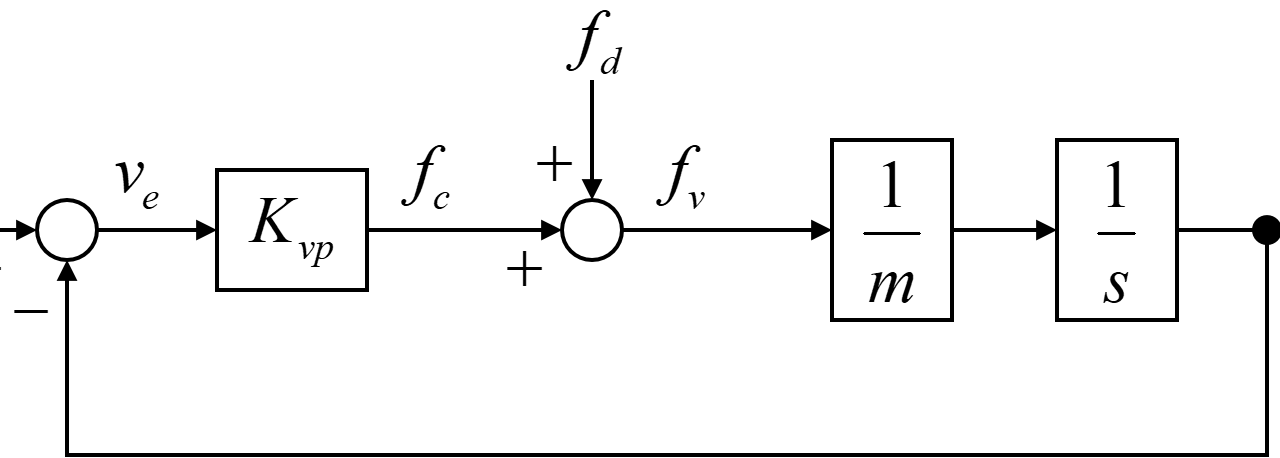





















 ELEGOO Arduinoスターターキット
ELEGOO Arduinoスターターキット

 UNO R3スマートロボットカー
UNO R3スマートロボットカー

 Raspberry Pi 3 Model b+
Raspberry Pi 3 Model b+
